Loudness perception
45 Intensity and Distance
Intensity and distance
As you move away from a sound source, the sound gets quieter- especially when you are outdoors. This is not surprising. Much like light, sound spreads out as it travels away from the source. Unless there are surfaces for the sound to reflect from, the sound’s intensity becomes less and less as you get further from the source.
Inverse square law and the paint can analogy
If you’ve ever used a can of spray paint, you know that distance is important- the closer you are to the nozzle, the more concentrated the paint stream is. Hold the can close to the surface you’re painting, you get a small spot of really thick paint. Hold the can further away and the same amount of paint gives a thinner coat that covers a larger area.
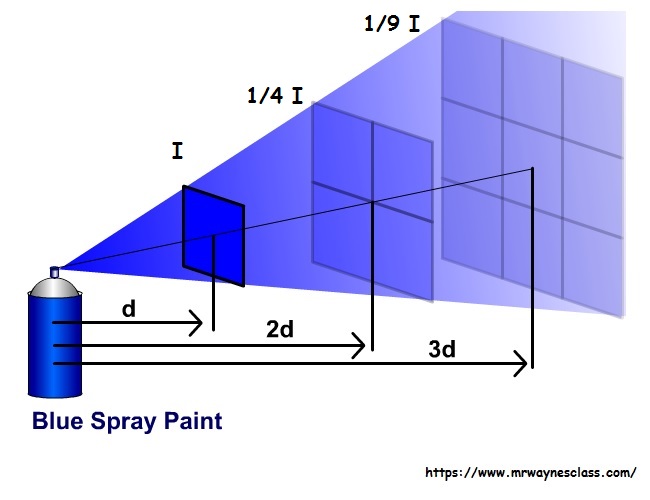
Suppose you squirt a dose of paint on a wall. You then deliver the same dose of paint from twice as far away and compare. How much larger is the new spot? How thick is the paint?
What did you answer? Twice the area? Half as thick? If you did, you got the answers wrong! Remember that area is length times width. Since the new paint spot is both twice as wide and twice as high as the original, it covers four times the area. As a result, the paint is only one quarter as thick as before. At triple the initial distance, the paint spot has nine times the original size and the paint is only one ninth as thick, and so on. In math speak, the concentration of the paint follows an inverse square law.
Sound radiating into open space works the same way. As you get farther and farther from the source, the power put out by the sound source gets spread over a larger and larger area. As a result, the sound intensity follows an inverse square law. Mathematically,
[latex]I \propto 1/d^2[/latex]
If you are uncomfortable with proportion notation, you can use the equation below instead:
[latex]\dfrac{I_2}{I_1}= \Big( \dfrac{d_1}{d_2} \Big)^2[/latex]
The picture below shows how it works. Notice that units are not given for distance. Because of the way that ratios work, any distance unit can be used. If you are two distance units from the source, the intensity is one fourth what the intensity is at one distance unit away from the source.

Stop to think 1
The sound intensity 1 foot away from a sound source is 200 μW/m2.
- What’s the intensity 2 feet away from the source?
- What’s the intensity 10 feet away from the source?
- What’s the intensity 6 inches away from the source?
Inverse square law and decibels
You can combine inverse square law and the rules of thumb for decibels. Each time distance is doubled, intensity is cut by a factor of four. Since each time intensity is cut in half the sound level decreases 3 dB, it follows that doubling distance reduces the sound level by 6 dB. Following the same logic, increasing the distance by a factor of ten reduces the sound level by 20 dB.
Stop to think 2
The sound level 1 foot away from a sound source is 70 dB.
- What’s the sound level 2 feet away from the source?
- What’s the level 10 feet away from the source?
- What’s the level 6 inches away from the source?
Example 1: Lawn mower sound intensity
Example: How intense is that lawn mower sound?
QUESTION:
When measured from 30 meters away, the intensity of a lawn mower’s sound is 10 μW/m2. What is the intensity at the lawn mower operator’s ears? (Assume the person operating the lawn mower is 1.5 meters tall).
SOLUTION:
Identify important physics concept: Sound intensity follows the inverse square law.
[latex]\dfrac{I_2}{I_1} = \Big( \dfrac{d_1}{d_2} \Big)^2[/latex]
List known and unknown quantities (with letter names and units):
[latex]I_2= \: ?[/latex]
[latex]I_1 = 10 \: \mu W/m^2[/latex]
[latex]d_2=1.5 \: meters[/latex]
[latex]d_1=30 \: meters[/latex]
Do the algebra: Solve the equation for [latex]I_2[/latex]. Move on to the next step.
Do unit conversions (if needed) then plug in numbers: None needed (because the units will cancel out):
[latex]I_2= I_1 \Big( \dfrac{d_1}{d_2} \Big)^2[/latex]
[latex]I_2= 10 \: \mu W/m^2 \Big( \dfrac{30 \: meters}{1.5 \: meters} \Big)^2[/latex]
[latex]I_2= 10 \: \mu W/m^2 (20)^2[/latex]
[latex]I_2= 4000 \: \mu W/m^2[/latex]
Reflect on the answer:
- The answer for intensity at the mower operator’s ears is larger than the intensity measured far away. That’s a good sign.
- The problem is much easier if you think in terms of ratios. Divide the two distances and you get the distance ratio- twenty in this case. Square the distance ratio to get the intensity ratio (four hundred).
- Even though the distance is twenty times closer, the intensity is four hundred times stronger.
Example 2: Lawn mower sound level
Example: Get away from that mower!
QUESTION:
When measured from 30 meters away, the sound level of a lawn mower’s sound is 70 dB. What is the sound level at the lawn mower operator’s ears? (Assume the person operating the lawn mower is 1.5 meters tall).
SOLUTION:
Identify important physics concepts:
- Sound intensity follows the inverse square law
[latex]I_2= I_1 \Big( \dfrac{d_1}{d_2} \Big)^2[/latex]
- Sound level is related to intensity by logs; you can use rules of thumb
- Double the intensity ==> add 3 dB to the sound level
- Ten times the intensity ==> add 10 dB to the sound level
List known and unknown quantities (with letter names and units):
[latex]SIL_2= \: ?[/latex]
[latex]SIL_1 = 70 \: dB[/latex]
[latex]d_2=1.5 \: meters[/latex]
[latex]d_1=30 \: meters[/latex]
Without a direct link from distance to SIL, you have to figure out intensity first and then apply the rules of thumb to link intensity to sound level.
Do the algebra: Do the algebra to find out about intensity first. Then use rules of thumb for the decibels.
Do unit conversions (if needed) then plug in numbers: None needed (because the units will cancel out):
[latex]\dfrac{I_2}{I_1}= \Big( \dfrac{d_1}{d_2} \Big)^2[/latex]
[latex]\dfrac{I_2}{I_1}= \Big( \dfrac{30 \: meters}{1.5 \: meters} \Big)^2=(20)^2[/latex]
[latex]\dfrac{I_2}{I_1}=400[/latex]
This means sound intensity at the ears is 400 times the intensity at the meter. Since 400 = 2 * 2 * 10 *10, the sound level is 26 dB higher (+3 dB + 3dB + 10 dB + 10dB) at the operator’s ears than the level at the meter. The level at the meter is 70 dB, so the level at the operator’s ears is 96 dB.
Reflect on the answer:
- The answer for sound level at the mower operator’s ears is larger than the level measured far away. That’s a good sign. The answer is less than the 130 dB sound level for jet plane- another good sign.
- There are easier ways to do the problem, especially if you think in terms of ratios and use rules of thumb. For instance, the distance ratio is 20:1. That means that the distance is “two times ten times away.” Doubling distance subtracts 6 dB from the level; multiplying distance by ten subtracts 20 dB. Dividing the distance by a factor of twenty adds 26 dB to the sound level.
Limitations
The math above applies to a point source in free field conditions. Point source refers to an ideal sound source that sends sound out equally in all directions. Real world sources actually do behave like point sources, provided you are far enough away. What qualifies for “far enough away” depends on the size of the source- a simple rule of thumb is multiply the length of the widest part of the source by five. For instance, the output from an audio speaker 1” across is similar to a point source if you are 5” (or more) away from it. Free field refers to an idealized environment where sound travels freely in all directions, without interacting with anything- imagine the entire universe entirely filled with air at uniform temperature (and nothing else). Even though the free field is a theoretical concoction, conditions similar to the near field do exist in real life- in rooms without much echo and very large, wide-open spaces (even if they have a floor).
Stop to think answers
- 50 μW/m2, 2 μW/m2 and 800 μW/m2. If your answers are 100, 20 and 400 μW/m2, you forgot the “square” in inverse square law.
- 64 dB, 50 dB and 76 dB. Doubling the distance cuts the level by 6 dB. Increasing the distance tenfold cuts the sound level by 20 dB.
Exa
Image Credits
- Paint can picture adapted from a ShockWave file [1] on Tony Wayne’s Teacher Resource webpage [2]
- Sound intensity picture created by Abbott.
