María Sierra-Paradinas^1.2 , Óscar Soto-Sánchez² , Antonio Alonso-Ayuso² , F. Javier Martín-Campo³ and Micael Gallego²

¹ IDOM Consulting, Engineering, Architecture, Spain

² Department of Computer Science, Computer Architecture, Computer Languages & Information Systems, Statistics & Operations Research, Universidad Rey Juan Carlos, Spain

³ Departamento de Estadística e Investigación Operativa, Instituto de Matemática Interdisciplinar, Universidad Complutense de Madrid, Spain

msierra@idom.com

Abstract. Cutting processes are an essential part of the activity of steel manufacturing companies. Among them is the slitting process where wide steel coils are slit into narrower coils, known as strips. A major challenge here is defining a slitting production plan that guarantees that the demand is met as well as minimizes the waste generated in the process. The planning is often carried out manually, taking several hours and allowing only a small part of the solution space to be explored. Although there is software available, it does not always meet with all the constraints and specifications of the process and custom software is a way of being able to include them. In this paper we will present a mathematical methodology to do the planning of a specific slitting process of a company in Europe that will help to develop a software solution for the company. The mathematical methodology, based in mixed integer linear optimization, will help reducing the amount of scrap generated in the process, improving customer orders’ fulfilment, reducing stock management costs, and saving time in the cutting planning process.

Keywords: Slitting, Steel Industry, Mixed Integer Linear Optimization.

1. Introduction

Cutting processes are an essential part of the activity of steel manufacturing companies. Among them is the slitting process wherein a wide steel coil is slit into narrower coils, knows as strips, with weights and widths specified by the customers.

In order to perform the slitting, the steel coil goes through the slitting machine where it is unwound and moved through circular blades, making the cuts. A diagram of the process can be seen in Fig. 1.

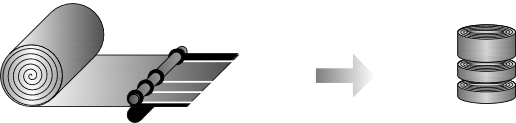
The planning of this process is mainly based on customer demand. Customers place orders for the strips, by specifying a certain width and a total weight. Then, the different orders are assigned to the available stock so that the leftovers generated in the process are minimized. This process of laying out cutting patterns so that the leftovers are minimized is also known as nesting.

As a result of nesting, a cutting production plan is obtained, indicating the number and size of strips that need to be cut from each coil. Nesting is often carried out manually, taking several hours and allowing only a small part of the solution space to be explored. Although there is nesting software available, it does not always meet with all the constraints and specifications of the process and custom software needs to be built.

In this paper, extracted from a previous work, we will present a mathematical methodology to do the nesting of a specific slitting process of a company in Europe. This methodology will help the company reducing the amount of scrap generated in the process, better adjusting the weight served for each order and reducing stock management costs. Furthermore, it will reduce the time used to prepare the cutting production plans and avoid mistakes caused by human errors, such as scheduling wrong quantities.

The remaining part of this paper is organized as follows. Section 2 presents some literature review regarding the type of problem we are facing. Section 3 introduces a detailed description of the problem under study. In Section 4 the mathematical methodology is introduced. Finally, Section 5 provides the conclusions obtained.

2. Literature review

Nesting is a classic problem known in the literature as the Cutting Stock Problem (CSP). CSPs can be summarized as problems when one needs to cut standard-sized pieces of stock material, into pieces of specified sizes so the waste generated is minimized. There are many variants of this problem depending on the dimension, the shape of the stock and pieces to be cut, the assortment and availability of stock material, the pattern restrictions, etc. A typology of CSPs can be seen in [1] and later extended in [2].

A simplified version of the problem presented in this work can be viewed as a generalization of the classical one-dimensional Cutting Stock Problem (1D-CSP). The coils held in stock have different widths and external diameters, in other words, the stock is heterogenous. The coils are then cut to produce strips to match the widths requested by the customers, considering that the number of blades used in the cutting process is limited.

However, unlike classical 1D-CSP, the orders do not specify the number of strips, instead they specify the total weight to be served for a specific strip width. The weight of the strip will depend on the selected coil and therefore it is not possible to know in advance the number of strips needed to meet the demand. CSPs with two relevant dimensions – where  one is fixed (the width of strips) and the other is variable (the weight) – are known as one-and-a-half-dimensional CSP (1.5D-CSP) (see [3]). This type of problem also differs from the 2D-CSP, where rectangles of a fixed length and width are cut from the rectangular stock.

Several authors have considered different versions of 1.5D-CSP. In [4] a 1.5D-CSP in the metal industry is presented. In [5] a 1.5D-CSP and assortment problem which involved determining the number of different widths of the rolls in stock and the cutting patterns used is studied. A detailed survey of 1.5D-CSPs from can be found in [6].

Another difference relative to the 1D-CSP is that the strips generated need to meet certain criteria, such as the maximum external diameter allowed. It can happen that the maximum external diameter allowed is smaller than the external diameter of the coil. In these cases, a guillotine crosscut needs to be done (from edge to edge) to reduce the diameter of the resulting strips to either by a half, a third and so forth, depending on the number of crosscuts performed.

Another characteristic of our problem is the assortment of coils. The coils held in stock are strongly heterogeneous. According to the extended typology of [2], our problem can be classified as a residual cutting stock problem (RSPC). In [7] it is argued that a traditional pattern-oriented approach is possible only when the stock is of the same size or of several standard sizes, thus inappropriate for this type of problem. There is a need to use item-oriented approaches, which are characterized by treating each item to be cut individually. Therefore, we propose an item-oriented approach based on a mixed integer linear optimization model.

When the coils are cut into the exact number of strips required, this may result in a large number of strips that are not assigned to any specific order. These are considered the leftovers of the process. Leftovers that are greater than a certain threshold are considered as usable leftovers and kept in stock, resulting in a stock very heterogenous. These problems where generating standard pieces for future use is possible is known as the Cutting Stock Problem with Usable Leftovers (see [8]). A survey can be found in [9]. We consider the leftovers of the process usable if they meet certain criteria and are preferred over generating scrap.

This paper studies the problem of the 1.5-dimensional residual cutting stock with usable leftovers (1.5D-RCSPUL), where crosscuts are permitted to reduce the diameter of resulting strips and knives constraints are considered. The stock consists of coils of different sizes containing leftovers from previous processes. Our aim is to find the cutting production plans that minimize the leftovers generated in the process while maximizing the overall accuracy of the orders.

3. Problem description

Nesting starts with the selection of orders that need to be satisfied and the selection of available stock of coils. As a result of the mathematical methodology the cutting production plan is defined:

• Selecting the coils from available stock to be used
• Defining the cutting patterns to perform in order to satisfy the orders

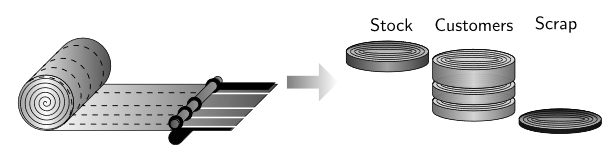
Then a combination of blades is set in the slitting machine to perform the cutting. Blades at both extremes are necessary to keep the coil uniform, therefore a minimum edge trim will always be required. Sometimes it will not be possible to use the whole coil to serve the orders, generating leftovers in the process. These leftovers may be usable and kept in stock if they meet specific criteria. Fig.  2a. shows the three types of products that can been obtained.

Orders are placed by customers by specifying a certain width and total weight. Customers may have restrictions that affect the way orders need to be served. These restrictions include the maximum weight of the strip and the maximum external diameter. These restrictions and the size of the coil chosen would define the number of strips served. To ensure each resulting strip has a certain weight that lies within the limits set by the customers it is possible to make one or more guillotine crosscuts with a shear blade, remaining the cutting pattern the same before and after the crosscut (see Fig. 2b). Each time a crosscut is carried out, it is possible to stop cutting a and rewound the remaining part. This is possible if the external diameter of the remaining part exceeds a certain value, in that case, it is kept in stock for future use (see Fig. 2c.).

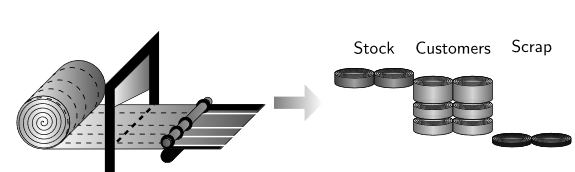
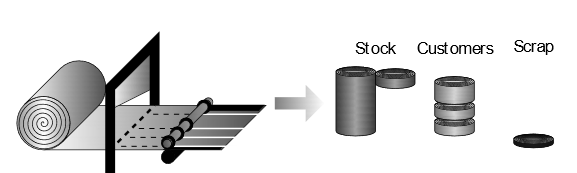
An additional feature of the problem is the compatibility of stock and orders.  The stock must be compatible with the quality requirements requested by the customer such as: type of material, thickness tolerance and quality parameter tolerances. This determines the set of compatible coils for each order. Nevertheless, due to the different tolerances of each order, the same coil can be used to serve orders with different characteristics, resulting in a problem that cannot be easily separated into sub-problems for each order’s typology.

Considering the characteristics of the problem, several cutting scenarios may arise, resulting in different types of cutting patterns which are shown in Fig. 3. The following situations may occur: (a) the strip width matches the coil width and the external diameter of the coil does not exceed the maximum external diameter allowed for the strip; (b) the strip width matches the coil width but the external diameter of the coil exceeds the maximum external diameter allowed for the strip and a crosscut need to be performed; (c) the strip width matches the coil width but the weight of the coil exceeds the weight ordered, a crosscut needs to be performed and part of the coil is rewound; (d) the strip width does not match the coil width, the coil is slit and at least two blades are needed for the edge trim; (e) the strip width does not match the coil width, the coil is slit and at least two blades are needed for the edge trim, besides the external diameter of the coil exceeds the maximum external diameter allowed for the strip and a crosscut need to be performed; and (f) the coil is slit and the weight of the coil exceeds the weight ordered, a crosscut needs to be performed and part of the coil is rewound.

4. Methodology

The methodology used is based in a Mixed Integer Linear programming model (MILP).  MILP models share the following components: decision variables that we seek to determine, an objective (goal) that we need to optimize (maximize or minimize) and constraints that the solution must satisfy [10]. Once we have the appropriate model, an algorithm is used to solve it in order to get an optimal solution. MILP models are those in which some of the variables can have only integer values and appear in the objective and constraints linearly. The two main algorithms to solve this type of problems are the Branch and Bound [11] and Cutting planes [12].

In the following, the main goals considered and the constraints taken into account to build the model, are detailed. The interested reader can find a detailed description of the implemented methodology in [13].

The goals pursued are:

• Minimize the leftovers generated in the process. The leftovers can be considered usable and kept in stock (retails) or discarded (scrap). Retails are preferred over scrap.
• Minimize the difference between the weight served and the weight that is ordered by each customer.
• Maximize the productivity of the cutting process.

The following constraints are considered in the model:

• All strips supplied should meet the customer’s requirements in terms of a maximum permitted weight and maximum external diameter allowed.
• The stock must satisfy all the quality requirements specified by the order.
• Both slits and guillotine crosscuts are considered for the cutting production plans.
• After a crosscut, the reconfiguration of blades is not allowed. Either the rest of the coil is cut with the same configuration or it is rewound and kept in stock. In the latter, the rewound part has to have at least certain external diameter.
• A minimum edge trim is required when slitting the coil.
• Customer’s orders must be fulfilled

The model has been implemented using the algebraic modeling language AMPL and solved using the MIP Gurobi v.9.0.2 optimizer. The objective function has been considered as a weighted sum of the three elements exposed above (leftovers, difference between the weight served and weight ordered, and productivity).

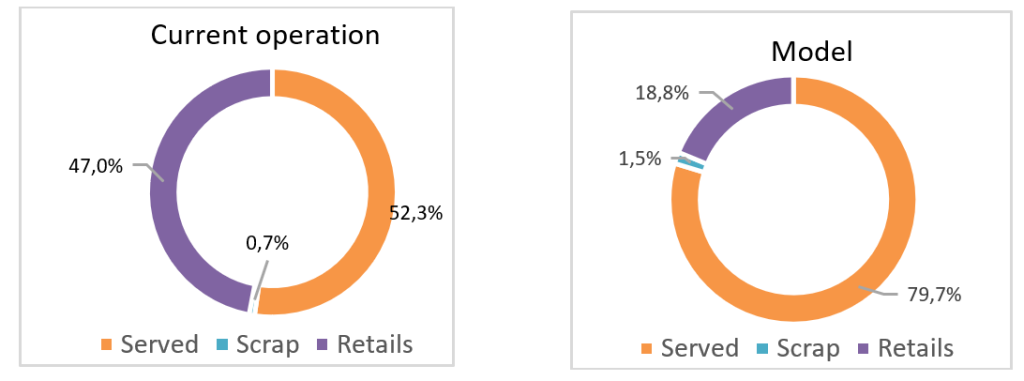
The methodology has been validated with instances provided by the company. The model was run for 10 minutes for each instance obtaining the optimal solution in 9 out of 11 instances. For the remaining two instances solutions were found with gaps smaller than 25 %.  In those cases, the solution provided by the model outperforms the results obtained by the company in the current operation.

The solution provided is the cutting production plan for the orders selected. In Fig. 4. the flowchart shows how the process works since the selection of orders and available stock until the cutting production plan is obtained.

In Fig. 5 the average consumption efficiency for the instances run is shown for both the current operation and the solution provided by the model.

5. Conclusions

The mathematical methodology presented has been used to solve the nesting of the slitting of a European company. The model has been validated with real data and has improved its current performance. In technical terms the model provides us with solutions that can increase the percentage of each coil that is dedicated to serve customer orders and decrease the retails accordingly. This fact also represents an improvement in the stock management, such as saving time in locating the coils as well as reducing the management costs of raw materials. Furthermore, the use of this mathematical methodology will mean a drastic reduction of planning times, the model is solved in only a few minutes, while the company needs several hours to prepare the current cutting plan.

References

1. Dyckhoff, H.: A typology of cutting and packing problems. European Journal of Operational Research 44, 145–159 (1990).
2. Wäscher, G., Hauβner, H., Schuman, H.: An improved typology of cutting and packing problems. European Journal of Operational Research 183(3), 1109–1130 (2007).
3. Hinxman, A.I.: The trim-loss and assortment problems: A survey. European Journal of Operational Research 5(1), 8–18 (1980).
4. Haessler, R. W.: A procedure for solving the 1.5-dimensional coil slitting problem. AIIE Transactions 10(1), 70–75 (1978)
5. Gasimov, R. N., Sipahioglu, A., Saraç, T.: A multi-objective programming approach to 1.5-dimensional assortment problem. European Journal of Operational Research 179(1), 64-79, (2007).
6. Sweeney, P. E., Paternoster, E. R.: Cutting and packing problems: A categorized, application-orientated Research bibliography. Journal of the Operational Research Society 43(7), 691–706, (1992)
7. Gradišar, M., Kljajić, M., Resinovič, G., Jesenko, J.: A sequential heuristic procedure for one-dimensional cutting. European Journal of Operational Research 114(3), 557–568, (1999).
8. Cherri, A. C., Arenales, M. N., Yanasse, H. H.: The one-dimensional cutting stock problem with usable leftover – a heuristic approach. European Journal of Operational Research 196(3), 897–908, (2009).
9. Cherri, A. C., Arenales, M. N., Yanasse, H. H., Poldi, K. C., Vianna, A. C. G.: The one-dimensional cutting stock problem with usable leftovers – A survey. European Journal of Operational Research 236(2), 395–402, (2014).
10. Taha, H.: Operations research: an introduction. Pearson Education Limited, Harlow, Essex, (2017).
11. Land, A. H., Doig, A. G.: An automatic method of solving discrete programming problems. Econometrica 28(3), 497-520, (1960)
12. Gomory, R. E.: Outline of an algorithm for integer solutions to linear programs. Bulletin of the American Mathematical Society 64(5), 275–278, (1958).
13. Sierra-Paradinas, M., Soto-Sánchez, Ó., Alonso-Ayuso, A., Martín-Campo, F.J., Gallego, M.: An exact model for a slitting problem in the steel industry. European Journal of Operational Research (2021, in press).