David Bogataj1,2![]() , Marija Bogataj1,2
, Marija Bogataj1,2![]() , Francisco Campuzano-Bolarín1
, Francisco Campuzano-Bolarín1![]() and José Andrés Moreno-Nicolás1
and José Andrés Moreno-Nicolás1![]()
1 Universidad Politécnica de Cartagena, Cartagena, Spain.
2 University of Ljubljana, SEB, Kardeljeva ploščad 17, 1000 Ljubljana, Slovenia.
Introduction
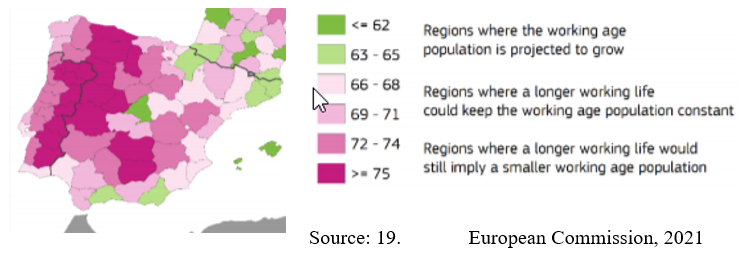
In the European Union, the number of people aged 65+ is growing from 91,3 million in 2019 to more than 130 million in 2060 (European Commission, 2021, 2021a). Figure 1 shows the required maximum working age in Spain and Portugal, which keeps the working-age population constant.
However, many older workers cannot work until they have reached the increased retirement age, often because of illness and latency. This phenomenon could be mitigated by increasing the retirement age with adequate disability insurance or I4.0 ergonomic support. New technologies, like the technologies of I4.0, should be appropriately introduced in the workplaces to keep productivity and reduce fatigue in the workplaces, avoiding musculoskeletal disorders and other exposures to risk of injury, physiological stress, and demotivation. To solve this problem, we have two basic options: (1) to develop and finance new supplementary occupational pension schemes or/and (2) to invest in I4.0 and other ergonomic improvements in the working places. Therefore, population ageing imposes additional tasks on managers: (1) to support pension insurance schemes for the early-retirement pension, (2) to consider the utilisation of disability insurance, (3) to improve ergonomics (Calzavara et al., 2020), (4) to invest in assisted technologies like collaborative robots, (5) to support the development of mini-factories and home cloud-manufacturing, (6) to introduce a new work design to utilise the highly skilled workers.
At nearly 50% of workplaces in Europe, productivity decreases by ageing, while at almost one-third of all workplaces, the productivity is neutral regarding ageing (Battini et al., 2017). But there is still 20% of activities where productivity increases by ageing in today’s technical environment. Suppose the retirement age will not increase, as suggested for Spain (Figure 1). The sustainability of pension systems requires raising the retirement age or decreasing pension benefits.
Objectives
In the article, we investigate how to systemise the trade-off between these options in a supply chain. The model is based on the Extended MRP theory (EMRP, Bogataj and Bogataj, 2019). It can autonomously evaluate balances between investments in ergonomics, robotics and I4.0 of workplaces or supporting decisions on occupational pension schemes and disability insurance. Disruptions and lower quality items produced by older workers in one activity cell of a supply chain can have a ripple effect throughout the entire chain (Bogataj et al., 2016). But also, value-added, personalised products and services often demand skilled and experienced older workers who need better ergonomic and other I4.0 technological support. Therefore, we must balance early retirement, which influences adequate pension and disability insurance schemes, and investments in ergonomics and new I4.0 technologies. The substantial decline of workers’ functional capacities in the production processes could expose the chain to the risk of robust delays and disruption (Bogataj et al., 2016). The visibility of planned flows in time and space and the proper evaluation of delayed production timing at each activity cell can be achieved when constructing the EMRP system, also in the case where the perturbations of timing appear simultaneously. Thus, EMRP enables forecasting, observing, and controlling the flows in a global supply chain (Bogataj et al., 2016, 2019). Previously, the Laplace transformed methods or z-transform discrete approaches, combined with Input-Output Analysis, were applied to formulating theoretical descriptions of MRP and related formulations of production flows (Grubbström, 2007) as inventories in the process and available inventories. The extension of this theory to the global supply chains was possible when the transportation matrix was introduced in the model, as presented by Bogataj and Grubbström (2012). Technologies that could have a substantial impact on production could be derived from approaches identified by Rüßmann et al. (2015) as follows: (a) Big Data Analytics (BDA), (b) Optimisation and Simulation (O&S), (c) Cloud Computing (CC), (d) Virtual and Augmented Reality (VR/AR), (e) Horizontal and Vertical System Integration (HVSI), (f) Internet of Things (IoT) in general with additional solutions for transportation and other logistics, and Industrial Internet of Things (IIoT) in production, (g) Additive Manufacturing (AM), (h) Autonomous Robots (ARobots), and (i) Cybersecurity (CS). We should also add Collaborative Robots (Cobots), which could substantially support older workers. A large gap could be noticed in the theory of ergonomics and I4.0 regarding the analysis of physical and psychosocial influences on latency and quality of production, giving specific methods and design guidelines for elderly workers. Consequently, future manufacturing and supply chains’ working environment should consider the expected decline of functional capacities regarding ageing and I4.0 support. Collaborative robots, exoskeletons and other I4.0 technologies will become a safe and productive help to reduce the seniors’ fatigue. How to formalise these phenomena is the question to which we shall answer here.
Methodology
Following the Net Present Value Theorem, the present value of the cash flow is obtained by replacing the frequency s with the continuous interest rate ρ, as developed by Grubbström (2007) and thereby the time preference can be embedded by the decision-maker in the model, where also the economic growth ω is assumed. The development of this theory is described by Bogataj and Bogataj (2019). We get the total NPV as the sum of production participation (NPVprod), discounted costs of ordering (NPVord) and wages (NPVw) and contributions to pension and disability funds (NPVr) and the relative part of wages excluded for investments in I4.0 (NPV14.0). NPV = NPVprod + NPVord+ NPVW + NPVr + NPV14.0 =
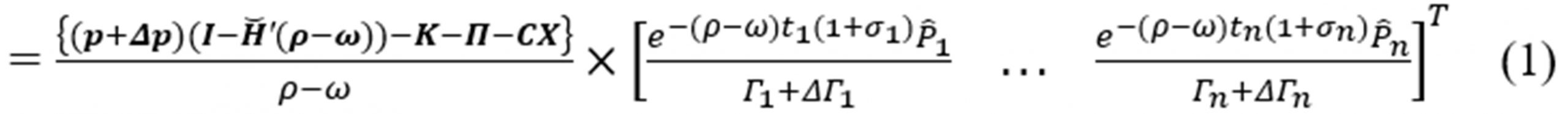 Here p is a vector of prices from the final product to the basic components, Δp is the possible change of prices due to the lower quality influenced by an ageing workforce, ρ is the interest rate, ω is economic growth,
Here p is a vector of prices from the final product to the basic components, Δp is the possible change of prices due to the lower quality influenced by an ageing workforce, ρ is the interest rate, ω is economic growth, ![]() is an input-output matrix of production and distribution,
is an input-output matrix of production and distribution, ![]() is production intensity vector in the i-th activity cell, K are setup costs, ∏ is the vector of transportation costs which appear when the item is transported from i, the Γ1 is the duration of cycle and ΔΓ1 is the delay of the cycle, the product ti(1 + σi) is the duration of i-th activity when disturbed by a factor (1 + σi), the product of vector C with the matrix X gives the cost of human resources, pension and disability insurance participation and the relative value of investments in the I4.0 improvements first calculated for the cycle so that divided by ρ-ω gives NPV, where ω is the expected growth of production and distribution (see Bogataj et al., 2016, 2019). It means that for each workplace in a node (i, i) and branch (i, j) we calculate the costs of labour CL,i,i and CL,i.j respectively, as well as the related percentage of it which goes to insurance funds CL,i,iαr,i,i and CL,i,jαr,i,j and percentage of it which goes to investments in I4.0 related to the nodes and branches in consideration CL,i,iαI4.0,i,i and CL,i,jαI4.0,i,j. Here αI4.0,i,i and αr,i,j are decision variables which influence δp, δiEi and δi,jEi,j as well as ΔΓ1 and σi and overall in ω.
is production intensity vector in the i-th activity cell, K are setup costs, ∏ is the vector of transportation costs which appear when the item is transported from i, the Γ1 is the duration of cycle and ΔΓ1 is the delay of the cycle, the product ti(1 + σi) is the duration of i-th activity when disturbed by a factor (1 + σi), the product of vector C with the matrix X gives the cost of human resources, pension and disability insurance participation and the relative value of investments in the I4.0 improvements first calculated for the cycle so that divided by ρ-ω gives NPV, where ω is the expected growth of production and distribution (see Bogataj et al., 2016, 2019). It means that for each workplace in a node (i, i) and branch (i, j) we calculate the costs of labour CL,i,i and CL,i.j respectively, as well as the related percentage of it which goes to insurance funds CL,i,iαr,i,i and CL,i,jαr,i,j and percentage of it which goes to investments in I4.0 related to the nodes and branches in consideration CL,i,iαI4.0,i,i and CL,i,jαI4.0,i,j. Here αI4.0,i,i and αr,i,j are decision variables which influence δp, δiEi and δi,jEi,j as well as ΔΓ1 and σi and overall in ω.
Therefore we, should calculate for each supply chain how these parameters depend on decision variables. In the numerical example, there is presented a supply chain bill of materials with timing in production units from the basic components E and F to the final product A. For this supply chain, we assumed that the activity node D assembles two units of items from E and one item of F. Activity node B requires three items of D for manufacturing one item of B; A needs one item B and two items C. The model without additional delays because of ageing worker (or shrinking lead times because of investments in I4.0) is explained in Bogataj and Grubbström (2012).
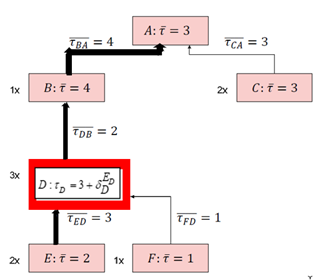
Now we shall assume how the ageing or investments influence NPV in such numerical example. For the basic assumption, we take that the quality does not change because of ageing, and therefore the prices of components and the final products in a supply chain are p = [560 38 25 34 14 15 ] € and transportation and setup costs are: K+Π = [200 180 210 195 175 215] €.
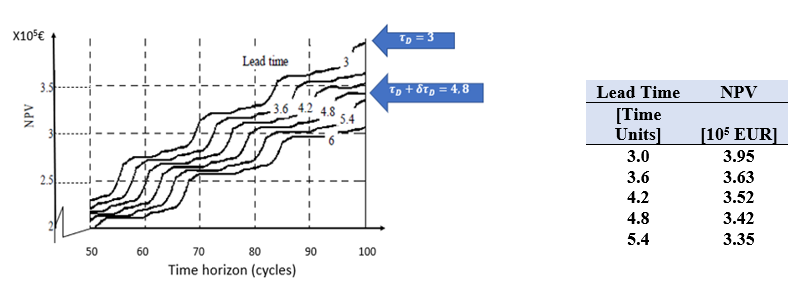
The variation of the NPV in case of variation of delays in D, where the older person was assumed to work, is presented in Fig. 3. We can see that in case of increasing latency, the lead time created in D grows from 3 to 4.8-time units, and when the time horizon is equal to 100 cycles, the NPV decreases from 395 000 € to 342 000 €. It means that it is advisable to invest in I4.0 technology to remove these delays.
It would remove or mitigate this delay economically if the investment’s net present value is lower than 53 000 €.
Conclusions
We can expect higher lead times and other delays in more than half of workplaces because of decreased functional capacities. In some workplaces, they also could produce with lower quality. It is also known that, at many workplaces, personalised productions and services often require skilled and experienced older workers because the younger human resources have not that experiences. These workers would stay in employment if they could get better I4.0 support. To balance these solutions, we suggest developing the simulation model based on the extended MRP Theory, where the trade-off between two options: (a) to create and finance occupational pension and disability schemes for compensation with early retirement or (b) to invest in an I4.0 technology for the improvement of the working places. We suggest correcting the final results by exploring the Network Simulation Model in the finite horizon operations (Sanchez-Perez et al., 2018). The proposed simulation model can autonomously evaluate investments in I4.0 technologies or search for a balance between participation in a new occupational pension scheme (also added disability insurance) and investment in the I4.0 technology.
Acknowledgement: This research has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 873077 (MAIA-H2020-MSCA-RISE 2019).
References
Bogataj, D., Aver, B., Bogataj, M.: Supply chain risk at simultaneous robust perturbations. Int. J. Prod. Econ., 181(A), 68-78 (2016).
Bogataj, D., Bogataj, M. NPV approach to material requirements planning theory: a 50-year review of these research achievements. International Int. J. Prod. Res, 57(15/16), 5137-5153, (2019).
Bogataj, D., Battini, D., Calzavara, M., Persona, A.: The ageing workforce challenge: investments in collaborative robots or contribution to pension schemes, from the multi-echelon perspective. International journal of production economics 210, 97-106 (2019a).
Bogataj, M., Grubbström, R.W.: On the representation of timing for different structures within MRP theory. Int. J. Prod. Econ., 140(2), 749–755 (2012).
European Commission: GREEN PAPER ON AGEING: Fostering solidarity and responsibility between generations. Brussels, COM(2021) 50 final. Available in January 27st, 2021. https://ec.europa.eu/info/sites/info/files/1_en_act_part1_v8_0.pdf (2021a).
Grubbström, R.W. 2007. Transform methodology applied to some inventory problems, Zeitschrift für Betriebswirtschaft. 77 (3): 297–324 (2007).
Rüßmann, M., Lorenz, M., Gerbert, P., Waldner, M., Justus, J., Engel, P., Harnisch, M.: Industry 4.0: the future of productivity and growth in manufacturing industries. Boston Consult. Group 9 (1), 54–89 (2015).
