Ester Guijarro1![]() , Eugenia Babiloni1
, Eugenia Babiloni1![]() and Juan R. Trapero2
and Juan R. Trapero2![]()
1 Universitat Politècnica de València, Camino de Vera s/n, 46022, Valencia. Spain.
2 Universidad de Castilla La Mancha, Avd. Camilo José Cela. 13071 Ciudad Real. Spain.
Keywords: Inventory; Continuous review; Expected shortage per replenishment cycle; Fill rate; Lost sales.
1. Introduction
This research focuses on the continuous review reorder point, base-stock (s, S) system for a lost sales case, which implies that unfulfilled demand is lost. In this system, the stock status is always known to guarantee that, when the stock reach a certain level or reorder point (ROP), a new replenishment order is launched. However, the implementation of continuous review policies entails two problems: (1) the length of the replenishment cycle is variable and (2) when demand is not unit sized, reaching exactly the ROP is not always probable and undershoots at ROP may appear. Common derivation of continuous inventory policies is based upon the assumption that undershoots at the reorder point are of negligible magnitude compared with the total lead time demand [1]. However neglecting undershoots affects the calculation of the on-hand stock levels that are overestimating especially in a lost sales context, and may lead to higher inventory costs or a lower service level than desired [2].
2. Objective
Different metrics exist to measure service levels, being the Fill Rate one of the most widely used in practice. The Fill Rate is defined as the fraction of customer demand that is met routinely; that is, without backorders or lost sales [1] and is normally computed in terms of units short [3], i.e. as the complementary of the ratio between the expected shortage per replenishment cycle (ESPRC further on) and the total demand. But, how the calculation of the ESPRC is affected by the hypothesis of neglecting undershoots? The objective of this paper is to answer this question and suggest a new approximation to compute the ESPRC that outperform the one based on neglecting undershoots.
3. The proposal of a new ESPRC method
In a (s, S) inventory system, we identify two feasible stockout situations: (i) when the on-hand stock is zero at the very moment the ROP is reached (Fig. 1 (a)). In this case the size of the undershoot is equal to the ROP; and (ii) when the on-hand stock is depleted once the ROP is reached and therefore the undershoot is equal to s – zt (Fig. 1 (b)). Therefore:
[latex]
ESPRC=\sum_{\tau = 0}^{s}\overline{P(z_\tau)}\cdot\left[\sum_{i=z_\tau}^{\infty}(i-z_\tau)\cdot f_L(i)\right]
[/latex]
Note that to compute accurately the ESPRC is necessary to know the probability distribution of the on-hand stock levels at τ (being τ the number of periods from the beginning of the cycle to the ROP).
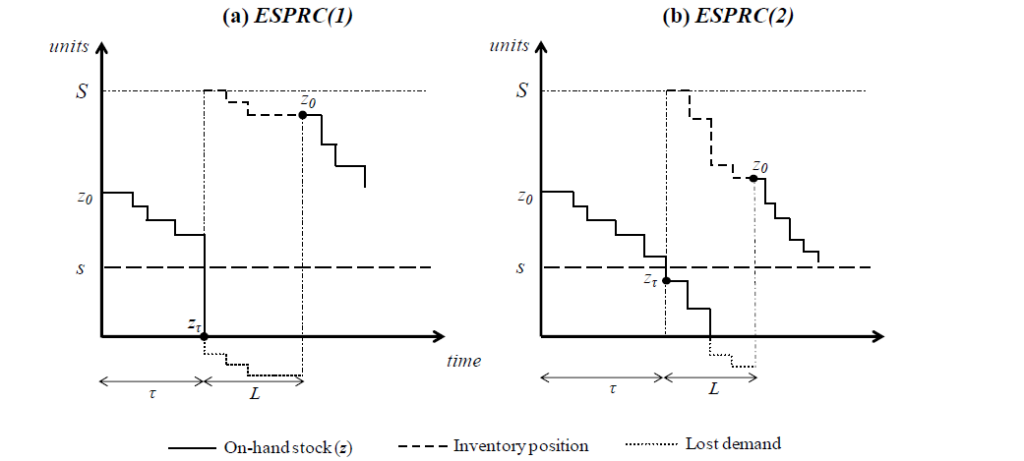
When undershoots are neglected (named ESPRCTrad), it is assumed that s = zt , and then the calculation of ESPRC becomes a close-form expression:
[latex]
ESPRC_{Trad}=\sum_{i=s+1}^{\infty}\left(i-s\right)\cdot f_L(i)
[/latex]
In this paper, we present a new approximate heuristic method to compute the ESPRC considering the possibility of undershoots at ROP. For that purpose, we approximate the probability vector of every value of the on-hand stock at ROP, taking into account that it is necessary: (1) to identify the non-zero values of P(zt) ; (2) to compute the cumulative probability of the feasible values of undershoots to find the non-zero positions of P(zt) ; and (3) to consider that the stock level at order delivery is always S, as an upper bound of the system which is a common hypothesis for the base-stock policies in lost sales contexts [4].
4. Conclusions
This paper analyses the difficulty of calculating ESPRC for a (s, S) inventory policy and lost sales context. Traditionally, the ESPRC assumes that order point is always reached exactly (i.e. undershoots are neglected), however this assumption is only possible if demand is unitary, which, if not, leads to a bias. To correct for this bias, we propose a new ESPRC approximation that implicitly considers the possibility of under- shoots and is based on approximating the probability vector of the stock levels when the order point is reached. The proposed method presents small relative errors and no apparent bias.
References
- Silver, E.A., Pyke, D.F., Peterson, R.: Inventory and Production Management in Supply Chains. Taylor and Francis Group (2017)
- Babiloni, E., Guijarro, E., Trapero, J.R.: A Non-parametric Enhancement of the Fill Rate Estimation. En: de Castro, R. y Giménez, G. (eds.) Advances in Engineering Networks. pp. 129-135. Springer International Publishing, Cham (2020)
- Tempelmeier, H.: On the stochastic uncapacitated dynamic single-item lotsizing problem with service level constraints. European Journal of Operational Research. 181, 184-194 (2007)
- Cardós, M., Guijarro, E., Babiloni, E.: On the estimation of on-hand stocks for base-stock policies and lost sales systems and its impact on service measures. International Journal of Production Research. 55, 4680-4694 (2017). https://doi.org/10.1080/00207543.2017.1279759
