10.3 Expected Value
In order to decide which alternative to select in a decision problem, we need a decision criterion; that is, a rule for making a decision. Expected value is a criterion for making a decision that takes into account both the possible outcomes for each decision alternative and the probability that each outcome will occur. To illustrate the concept of expected value, we consider a simpler decision with lower stakes than the Special Instrument Products decision.
Example 10.4
If a six-sided die is fair, there is a [latex]\frac{1}{6}[/latex] probability that any specified side will come up on a roll. Therefore there is a [latex]\frac{4}{6}[/latex] = [latex]\frac{2}{3}[/latex] probability that a 3, 4, 5, or 6 will come up and you will win. Figure 10.3 shows the decision tree for one play of this game.
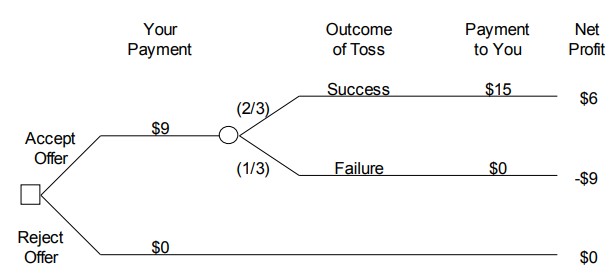
Figure 10.3 Die toss decision tree
At first glance, this may not look like a good bet since you can lose $9.00, while you can only win $6.00. However, the probability of winning the $6.00 is [latex]\frac{2}{3}[/latex], while the probability of losing the $9.00 is only [latex]\frac{1}{3}[/latex]. Perhaps this isn t such a bad bet after all since the probability of winning is greater than the probability of losing. The key to logically analyzing this decision is to realize that your friend will let you play this game as many times as you want. For example, how often would you expect to win if you play the game 1,500 times? Based on what you have learned about probability, you know that the proportion of games in which you will win over the long run is approximately equal to the probability of winning a single game. Thus, out of the 1,500 games, you would expect to win approximately [latex]\frac{2}{3}[/latex] X 1,500 = 1,000 times. Therefore, over the 1,500 games, you would expect to win a total of approximately 1,000 X $6 + 500 X (-$9) = $1,500. So this game looks like a good deal!
Based on this logic, what is each play of the game worth? Well, if 1,500 plays of the game are worth $1,500, then one play of the game should be worth $1,500/1,500 = $1.00. Putting this another way, you will make an average of $1.00 each time you play the game. A little thought about the logic of these calculations shows that you can directly determine the average payoff from one play of the game by multiplying each possible payoff from the game by the probability of that payoff, and then adding up the results. For the die tossing game, this calculation is [latex]\frac{2}{3}[/latex] X $6 + [latex]\frac{1}{3}[/latex] X (-$9) = $1.
The quantity calculated in the manner illustrated in Example 10.4 is called the expected value for an alternative, as shown in Definition 10.2. Expected value is often a good measure of the value of an alternative since over the long run this is the average amount that you expect to make from selecting the alternative.
Definition 10.2: Expected Value
Example 10.5 Product decision.
alternative with the highest expected value is developing the temperature sensor, and if the expected value criterion is applied, then the temperature sensor should be developed.
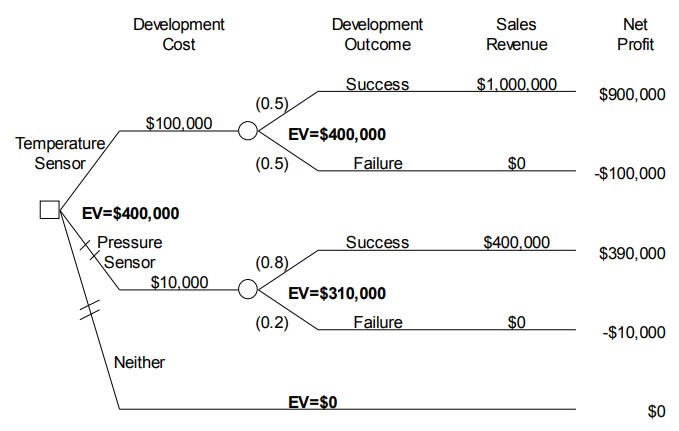
Figure 10.4 Special Instrument Products decision tree, with expected values
Figure 10.4 illustrates some additional notation that is often used in decision trees. The branches representing the two alternatives that are less preferred are shown with crosshatching (//) on their branches. The expected value for each chance node is designated by EV. Finally, the expected value at the decision node on the left is shown as equal to the expected value of the selected alternative.
Xanadu Traders
We conclude this section by analyzing a decision involving international commerce. This example will be extended in the remainder of this chapter.
Example 10.6 Xanadu Traders
Xanadu Traders, a privately held U.S. metals broker, has acquired an option to purchase one million kilograms of partially refined molyzirconium ore from the Zeldavian government for $5.00 per kilogram. Molyzirconium can be processed into several different products which are used in semiconductor manufacturing, and George Xanadu, the owner of Xanadu Traders, estimates that he would be able to sell the ore for $8.00 per kilogram after importing it. However, the U.S. government is currently negotiating with Zeldavia over alleged dumping of certain manufactured goods which that country exports to the United States. As part of these negotiations, the U.S. government has threatened to ban the import from Zeldavia of a class of materials that includes molyzirconium. If the U.S. government refuses to issue an import license for the molyzirconium after Xanadu has purchased it, then Xanadu will have to pay a penalty of $1.00 per kilogram to the Zeldavian government to annul the purchase of the molyzirconium. Xanadu has used the services of Daniel A. Analyst, a decision analyst, to help in making decisions of this type in the past, and George Xanadu calls on him to assist with this analysis. From prior analyses, George Xanadu is well-versed in decision analysis terminology, and he is able to use decision analysis terms in his discussion with Analyst.
Analyst: As I understand it, you can buy the one million kilograms of molyzirconium ore for $5.00 a kilogram and sell it for $8.00, which gives a profit of ($8.00 – $5.00) X 1,000,000 = $3,000,000. However, there is some chance that you cannot obtain an import license, in which case you will have to pay $1.00 per kilogram to annul the purchase contract. In that case, you will not have to actually take the molyzirconium and pay Zeldavia for it, but you will lose $1.00 X 1,000,000 = $1,000,000 due to the cost of annulling the contract.
Xanadu: Actually, some chance may be an understatement. The internal politics of Zeldavia make it hard for their government to agree to stop selling their manufactured goods at very low prices here in the United States. The chances are only fifty-fifty that I will be able to obtain the import license. As you know, Xanadu Traders is not a very large company. The $1,000,000 loss would be serious, although certainly not fatal. On the other hand, making $3,000,000 would help the balance sheet…
Question 10.3: Which alternative should Xanadu select?
Assume that Xanadu uses expected value as his decision criterion. To answer this question, construct a decision tree. There are two possible alternatives, purchase the molyzirconium or don’t purchase it. If the molyzirconium is purchased, then there is uncertainty about whether the import license will be issued or not. The decision tree is shown in Figure 10.5. Starting from the root node for this tree, it costs $5 million to purchase the molyzirconium, and if the import license is issued, then the molyzirconium will be sold for $8 million, yielding a net profit of $3 million. On the other hand, if the import license is not issued then Xanadu will recover $4 million of the $5 million that it invested, but will lose the other $1 million due to the cost of annulling the contract. The endpoint net profits are shown in millions of dollars, and the expected value for the purchase alternative is 0.5 X $3 + 0.5 X (-$1) = $1, in millions of dollars. Therefore, if expected value is used as the decision criterion, then the preferred alternative is to purchase the molyzirconium.
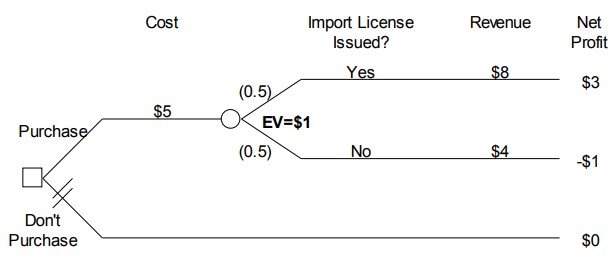
Figure 10.5 Xanadu Traders initial decision tree (dollar amounts in millions)
Attribution
By Craig W. Kirkwood, Chapter 1 of Decision Tree Primer, January 11, 2013, licensed under a Creative Commons Attribution License CC BY-NC-SA 4.0.
