10.4 Dependent Uncertainties
In this section, we consider an additional complexity that often occurs in business decisions: dependent uncertainties. Specifically, we will examine a case that illustrates this complexity of real world decisions, and review a procedure for analyzing decisions that include dependent uncertainties.
Example 10.7 Xanadu Traders
This is a continuation of Example 10.6. We now consider an expanded version of the decision that includes dependent uncertainties and extend the analysis procedure to handle this new issue. We continue to follow the discussion between Daniel Analyst and George Xanadu that started in Example 10.6.
Analyst: Maybe there is a way to reduce the risk. As I understand it, the reason you need to make a quick decision is that Zeldavia has also offered this deal to other brokers, and one of them may take it before you do. Is that really very likely? Perhaps you can apply for the import license and wait until you know whether it is approved before closing the deal with Zeldavia.
Xanadu: That s not very likely. Some of those brokers are pretty big operators, and dropping $1,000,000 wouldn’t make them lose any sleep. I’d say there is a 0.70 probability that someone else will take Zeldavia’s offer if I wait until the import license comes through. Of course, it doesn’t cost anything to apply for an import license, so maybe it is worth waiting to see what happens.
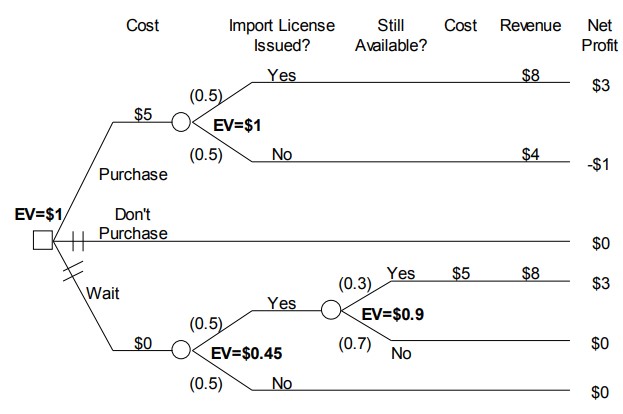
Figure 10.6 Xanadu Traders revised decision tree, with expected values
The decision tree for this revised problem is shown in Figure 10.6. The two alternatives at the top of this tree ( purchase and don t purchase ) are the same as the alternatives shown in Figure 10.5. The third alternative ( wait ) considers the situation where Xanadu waits to see whether it can obtain an import license before purchasing the molyzirconium. This alternative introduces a new analysis issue that must be addressed before the expected value for this alternative can be determined. This new issue concerns the fact that there are two stages of
uncertainty for this alternative. First, the issue of an import license is resolved, and then there is a further uncertainty about whether the molyzirconium will still be available.
The process of determining the expected value for this alternative involves two stages of calculation. In particular, it is necessary to start at the right side of the decision tree, and carry out successive calculations working toward the root node of the tree. Specifically, first determine the expected value for the alternative assuming that the import license is issued, and then use this result to calculate the expected value for the wait alternative prior to learning whether the import license is issued.
Examine Figure 10.6 to see how this calculation process works. As this figure shows, if the import license is issued, then there is a 0.3 probability that the molyzirconium will still be available. In this case, Xanadu will pay $5 million for the molyzirconium, and sell it for $8 million realizing $3 million in net profit. If the molyzirconium is not still available, then Xanadu will not have to pay anything and will realize no net profit. Thus, the expected value for the situation after the uncertainty about the import license has been resolved is 0.3 X $3 + 0.7 X
$0 = $0 9. This expected value is shown next to the lower right chance node on the decision tree in Figure 10.6.
From the discussion regarding expected value in Section 10.2, it follows that this $0.9 million is the value of the alternative once the result of the import license application is known. Hence, this value should be used in the further expected value calculation needed to determine the overall value of the wait alternative. Thus, the expected value for the wait alternative is given by 0.5 X $0.9 + 0 5 X $0 = $0.45. This expected value is shown next to the lower left chance node on the decision tree in Figure 10.6. Since the expected value for the wait alternative is less than the $1 million expected value for purchasing the molyzirconium right now, this alternative is less preferred than purchasing the molyzirconium right now. Xanadu should not wait, assuming that expected value is used as the decision criterion.
The process of sequentially determining expected values when there are dependent uncertainties in a decision tree, as demonstrated in Example 10.6, is called decision tree rollback. This term is defined in Definition 10.3.
Definition 1.3: Decision Tree Rollback
The process of successively calculating expected values from the endpoints of the decision tree to the root node, as demonstrated in this section, is called a decision tree rollback.
Attribution
By Craig W. Kirkwood, Chapter 1 of Decision Tree Primer, January 11, 2013, licensed under a Creative Commons Attribution License CC BY-NC-SA 4.0.
