2.22 Spot Rates
The reinvestment rate for the MIRR is exogenous or external; so far for us, in other words, it was a “given.” The analyst must project the project’s reinvestment rate, based on economic and financial matters about which he is aware within the corporation’s business environment. Absent such information, s/he must, obviously, look elsewhere.
Some useful clues may be garnered from the bond yield curve, which embeds critical information about future short-term interest rates. The “spot curve,” which we delineate below, will provide not merely a single future reinvestment rate, but multiple and varying rates over the term of the project. The provision of varying reinvestment rates will satisfy the claim that future rates cannot be monolithic.
Example I:
1.5-Year Treasury Bond
Price = 99.45 ( Par = 100)
Coupon = .085
6-Month Zero YTM = .08
1-Year Zero YTM = .083
- What is the theoretical 1.5-year Spot Rate (yB3)?
Solution:
Coupon Payments = ($100) (.085) (.5) = $4.25

Where y1 = (.080) (.5)
Where y2 = (.083) (.5)
Where y3 = ?
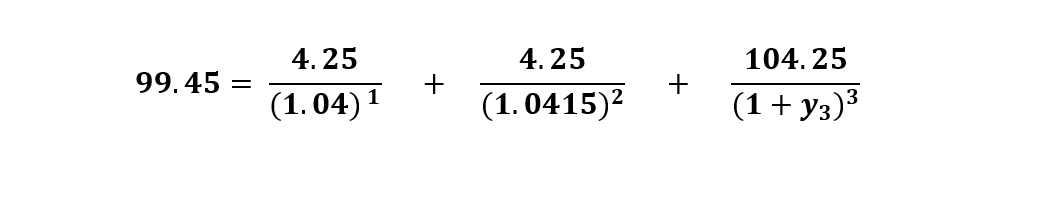
y3 = .04465
BEY3 = (2) (.04465) = .0893
Where BEY = Bond Equivalent Yield
Example II:
2.0 Year Treasury Bond
Price = 99.64 (Par = 100)
Coupon = .090
Spot Rates for y1 – y3 as in Example #1 above
- What is the theoretical 2.0-year Spot Rate (y4)?
Solution:
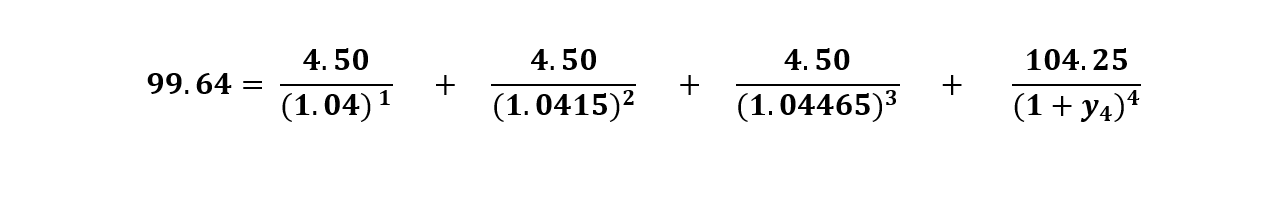
y4 = .046235
BEYy4 = (2) (.046235) = .09247
Summary:
| Maturity | Coupon | Price | Y-T-M | Spot Rates |
| 6- months | 0.00% | 96.15 | .0800 | .08000 |
| 1-year | 0.000 | 92.19 | .0830 | .08300 |
| 1.5 -years | 0.085 | 99.45 | .0890 | .08930 (As calculated) |
| 2.0- years | 0.090 | 99.64 | .0920 | .09247 (As calculated) |
Can you graph this?
- Show the terms-to-maturity on the horizontal.
- Show the yields for the two curves on the vertical.
- Note that, in this case, the curves diverge after one-year.
