Magnetism
UNIT 27 – Sources Of Magnetic Fields
Last Update: 07/08/2024
the magnetic field produced by currents
In the preceding chapter, we saw that a moving charged particle produces a magnetic field. This points to a fundamental connection between electricity and magnetism. In this unit, we discuss the properties of the magnetic fields generated by currents.
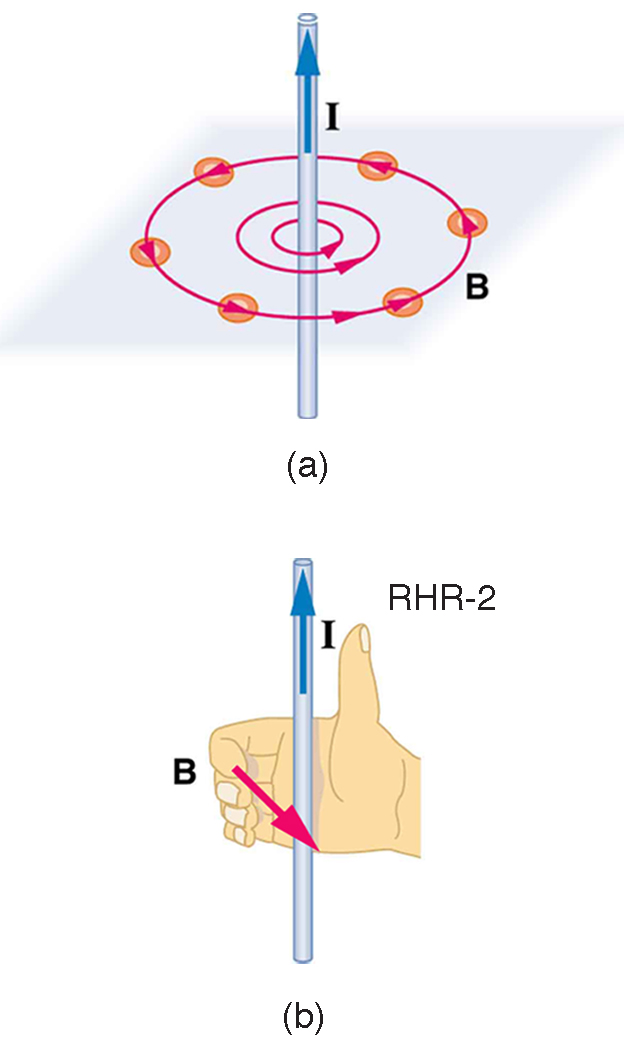
the magnetic field of a long straight current-carrying wire
The field around a long straight wire is found to be in circular loops. The direction of the field is determined by using another version of the Right-Hand-Rule —point the thumb in the direction of the current, and the fingers curl in the direction of the magnetic field loops created by it. This is demonstrated in Figure 27.1. And the magnitude of the magnetic field is given by the equation below.
 |
In this equation
|
Example 27.1
Find the current in a long straight wire that would produce a magnetic field twice the strength of the Earth’s at a distance of 5.0 cm from the wire.
Solution
The Earth’s field is about 5.0×10-5T.
![]()
![]()
![]()
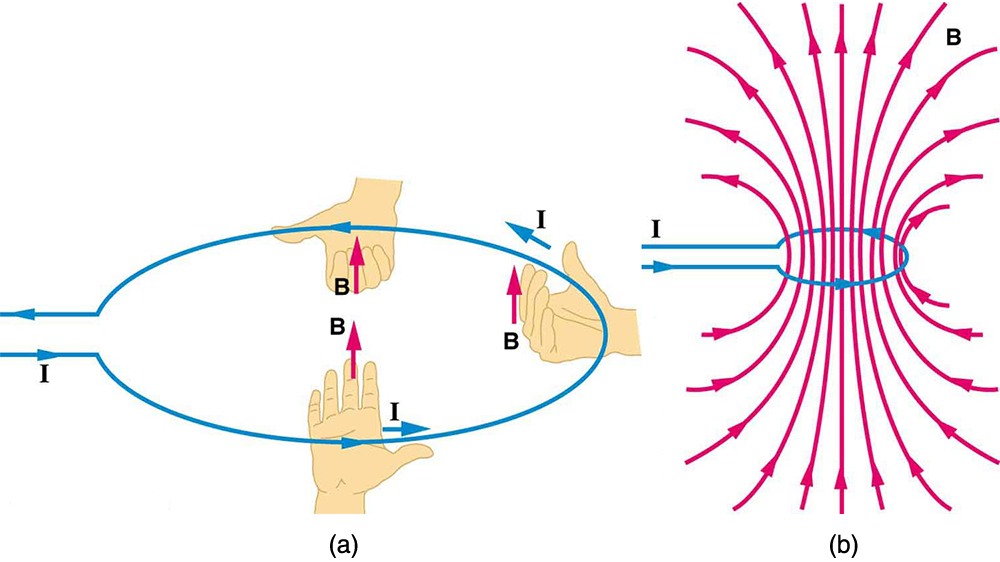
magnetic field of a current carrying circular loop
The magnetic field near a current-carrying loop of wire is shown in Figure 27.2. Both the direction and the magnitude of the magnetic field produced by a current-carrying loop are complex. Right-Hand-Rule can be used to give the direction of the field near the loop. There is a simple formula for the magnetic field strength at the center of a circular loop.
 |
In this equation
|
One way to get a larger field is to have N loops; then, the field is ![]() Note that the larger the loop, the smaller the field at its center, because the current is farther away.
Note that the larger the loop, the smaller the field at its center, because the current is farther away.
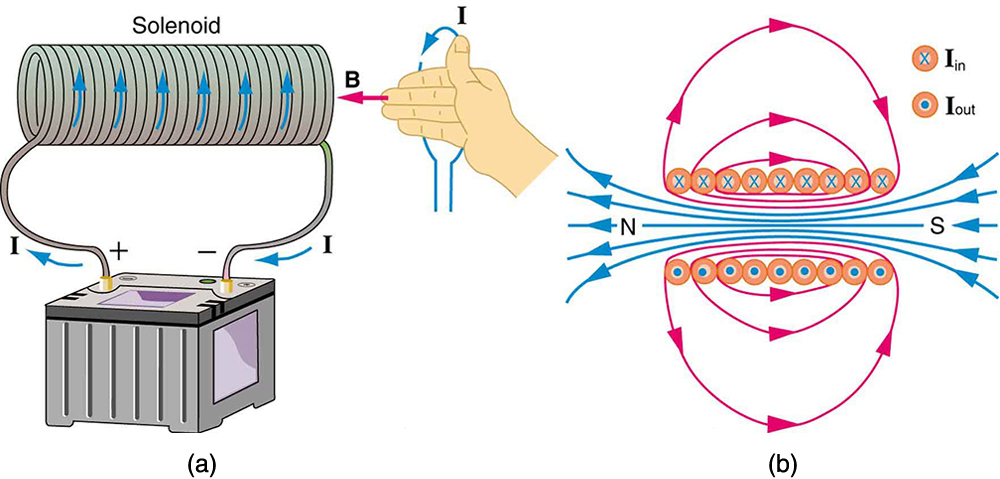
the magnetic field of a current-carrying solenoid
A solenoid is a long coil of wire with many turns or loops, as opposed to a flat loop. Because of its shape, the field inside a solenoid can be very uniform, and also very strong. The field just outside the coils is nearly zero. Figure 27.3 shows how the field looks and how its direction is given by Right-Hand-Rule.
 |
In this equation
|
The magnetic field inside of a current-carrying solenoid is very uniform in direction and magnitude. Only near the ends does it begin to weaken and change direction. The field outside has similar complexities to flat loops and bar magnets. Notice that ![]() is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform fields spread over a large volume are possible with solenoids, as Example 27.2 implies.
is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform fields spread over a large volume are possible with solenoids, as Example 27.2 implies.
Example 27.2
What is the field inside a 2.00-m-long solenoid that has 2000 loops and carries a 1600-A current?
Solution
We need to first find n, the number of loops per unit length.
![]()
![]()
![]()
The magnetic field inside this solenoid is
![]()
![]()
![]()
Discussion
This is a large field strength that could be established over a large-diameter solenoid, such as in medical uses of magnetic resonance imaging (MRI). The very large current is an indication that the fields of this strength are not easily achieved, however. Such a large current through 1000 loops squeezed into a meter’s length would produce significant heating. Higher currents can be achieved by using superconducting wires, although this is expensive. There is an upper limit to the current since the superconducting state is disrupted by very large magnetic fields.
the magnetic force between two parallel currents
The force between two long straight and parallel conductors separated by a distance r can be found by applying what we have developed in the preceding sections. Figure 27.4 shows the wires, their currents, the fields they create, and the subsequent forces they exert on one another. Let us consider the field produced by wire 1 and the force it exerts on wire 2 (call the force F2). The field due to I1 at a distance r is given to be
![]()
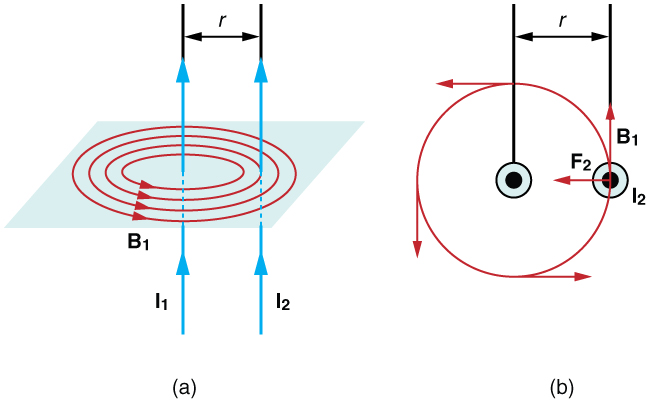
This field is uniform along wire 2 and perpendicular to it, and so the force F2 it exerts on wire 2 is given by ![]() with
with ![]() .
.
![]()
By Newton’s third law, the forces on the wires are equal in magnitude, and so we just write F for the magnitude of F2. Since the wires are very long, it is convenient to think in terms of force per unit length, ![]() . Substituting the expression forB1 into the last equation and rearranging terms gives
. Substituting the expression forB1 into the last equation and rearranging terms gives
![]()
![]() is the force per unit length between two parallel currents
is the force per unit length between two parallel currents ![]() and
and ![]() separated by a distance
separated by a distance ![]() . The force is attractive if the currents are in the same direction and repulsive if they are in opposite directions.
. The force is attractive if the currents are in the same direction and repulsive if they are in opposite directions.
Example 27.3
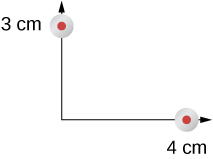
Two wires, both carrying current out of the page, have a current of magnitude 5.0 mA. The first wire is located at (0.0 cm, 3.0 cm) while the other wire is located at (4.0 cm, 0.0 cm) as shown in Figure 27.5. What is the magnetic force per unit length of the first wire on the second and the second wire on the first?
Solution
First we need to find the distance between the two wires.
![]()
![]()
The force per unit length between the two current carrying wires is
![]()
![]()
![]()
These wires produce magnetic fields of equal magnitude but opposite directions at each other’s locations. Whether the fields are identical or not, the forces that the wires exert on each other are always equal in magnitude and opposite in direction (Newton’s third law).
Attribution
This chapter contains material taken from Openstax College Physics -Magnetism, and Openstax University Physics Volume 2-Sources of Magnetic Fields and is used under a CC BY 4.0 license. Download these books for free at Openstax
To see what was changed, refer to the List of Changes.
Questions and problems
questions
- What is the source of magnetism?
Problems
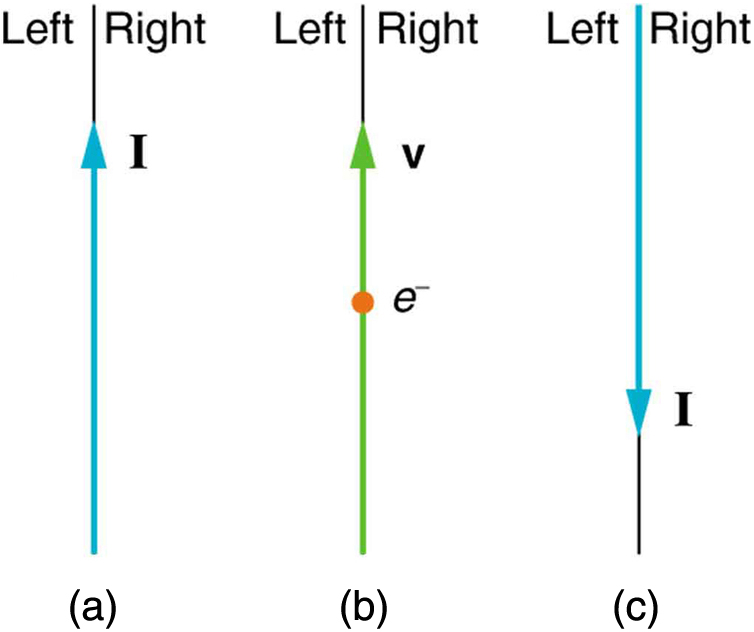
- [openstax college physics – 22.58] Indicate whether the magnetic field created in each of the three situations shown below is into or out of the page on the left and right of the current.
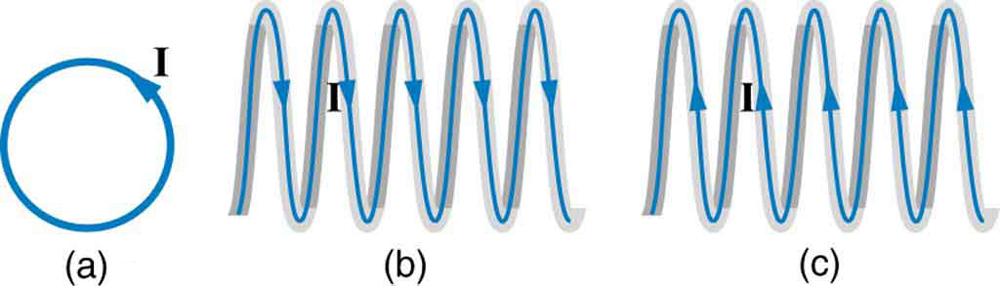
- [openstax college physics 22.59] What are the directions of the fields in the center of the loop and coils shown below?
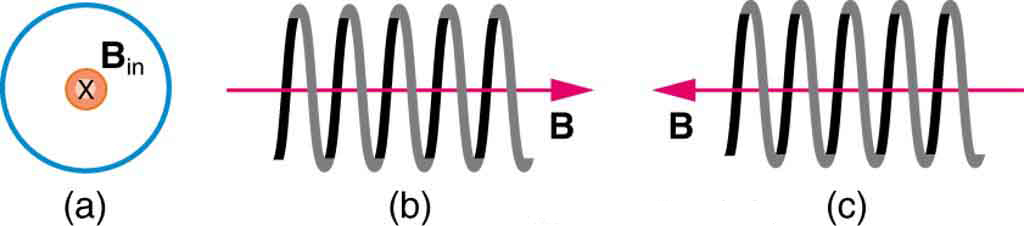
- [openstax college physics 22.60] What are the directions of the currents in the loop and coils shown below?
- [openstax college physics 22.62] Inside a motor, 30.0 A passes through a 250-turn circular loop that is 10.0 cm in radius. What is the magnetic field strength created at its center?
- [openstax college physics 22.64] How strong is the magnetic field inside a solenoid with 10,000 turns per meter that carries 20.0 A?
- [openstax college physics 22.57] The figure below shows a long straight wire near a rectangular current loop. What is the direction and magnitude of the total force on the loop?
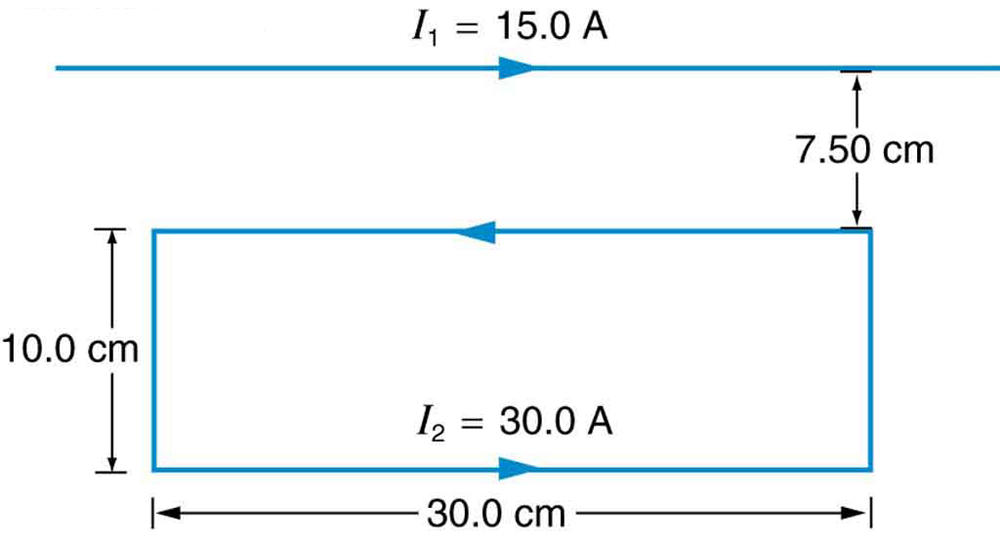
fig-prob27.6 [Image Description] - [openstax college physics 22.66] How far from the starter cable of a car, carrying 150 A, must you be to experience a field less than the Earth’s (5.00×10-5T). Assume a long straight wire carries the current. (In practice, the body of your car shields the dashboard compass.)
image descriptions
fig-prob27.6 image description – A rectangular wire with dimensions 30.0cm X 10.0cm carries a counterclockwise current, I2=30.0A. A wire, parallel to the long end of the rectangle and 7.50cm away, carries a current I1=15.0A to the right. [Return to the image]
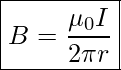 Magnetic Filed Of A Long Straight Current
Magnetic Filed Of A Long Straight Current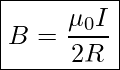 Magnetic Filed At The Center Of A Current Loop
Magnetic Filed At The Center Of A Current Loop