Unit 14 – Rotational Kinetic Energy and Moment of Inertia

Beta Keramati

Rotational Motion

Last Update: 12/06/2022

Rotational motion and angular velocity

So far in this text, we have mainly studied translational motion, including the variables that describe it: displacement, velocity, and acceleration. Now we expand our description of motion to rotation—specifically, rotational motion about a fixed axis. We will find that rotational motion is described by a set of related variables similar to those we used in translational motion.

rotation angle

When objects rotate about some axis—for example, when the CD (compact disc) in Figure 14.1 rotates about its center—each point in the object follows a circular arc. Consider a line from the center of the CD to its edge. See the line OA in Figure 14.2. Each pit used to record sound along this line moves through the same angle in the same amount of time. When the CD rotates through an angle ΔΘ, the line segment OA moves to OB. The rotation angle ΔΘ in radian is defined as the ratio of the arc length, Δs, to the radius of curvature, r.

$\Delta \theta = \frac{\Delta S}{r}$

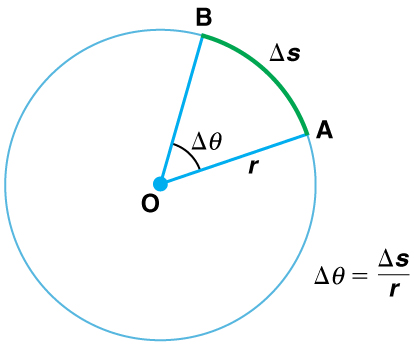The arc, Δs is the distance traveled along a circular path as shown in Figure 14.2.

Angular velocity

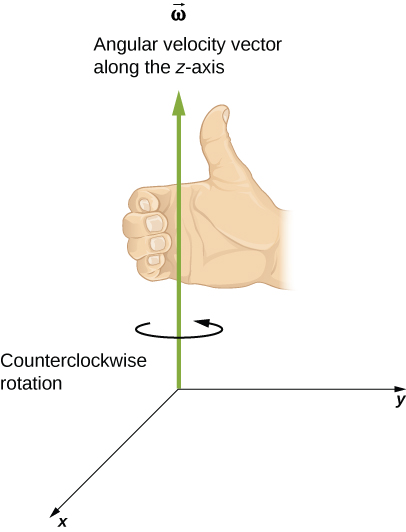
We define angular velocity, $\vec \omega$ , as the rate of change of an angle. The direction of angular velocity is determined by the right-hand rule. The right-hand rule is such that if the fingers of your right hand wrap in the direction that the angle Θ is increasing, your thumb points in the direction of the angular velocity. This is demonstrated in Figure 14.3. We often use positive and negative to denote the direction of the angular velocity vector. Since a counterclockwise rotation in the x-y plane corresponds to an angular velocity in the positive z-direction (as shown in Figure 14.3), we denote the angular velocity as positive when the rotation is counterclockwise, and negative when it is clockwise.

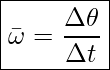Average angular velocity has a magnitude given by

$\boxed{\bar \omega=\frac{\Delta \theta}{\Delta t}}$ Average Angular Velocity

In the SI system of units, angular velocity is measured in units of radian per second (rad/s).

Since $\Delta \theta = \frac{\Delta S}{r}$ we can easily find the relationship between, average angular speed, $\bar\omega$ , and average linear speed, $\bar v=\frac{\Delta S}{\Delta t}$ .

$\bar\omega=\frac{1}{r} \frac{\Delta S}{\Delta t}$

$\bar\omega=\frac{1}{r}\bar v$

A similar relationship exists between the magnitudes of the instantaneous angular velocity and linear velocity. In other words

$\boxed{\omega=\frac{1}{r}v\ ,\ v=r\omega}$

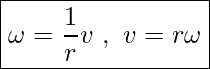
Consider a rotating disk as shown in Figure 14.4. Points 1 and 2 rotate through the same angle ΔΘ but point 2 moves through a greater arc length ΔS because it is at a greater distance from the center of rotation (r₂>r₁). This means that points that are closer to the center of the disk have smaller linear speeds than the points farther away from the center as shown in Figure 14.5, even though all points sweep out the same angle in the same amount of time and have equal angular speeds. Since all points on a rotating object have the same angular speed, it is much more convenient to use angular speed when describing rotation.

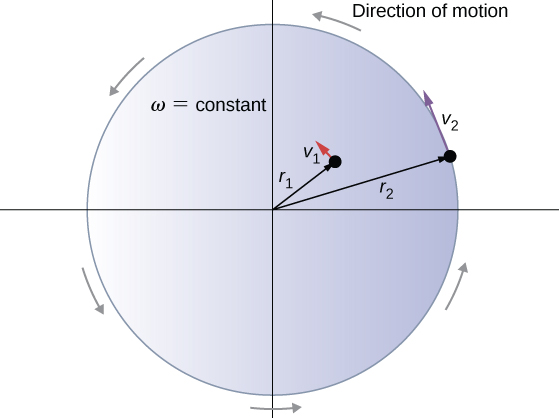Example 14.1

A flywheel rotates with an angular velocity of 45.0rad/s in a counterclockwise direction.

(a) How many radians does the flywheel rotate through in 30.0 s?

(b) What is the tangential speed of a point on the flywheel 10.0 cm from the axis of rotation?

Solution for (a)

Since the flywheel has a constant rotational velocity, there is no difference between average and instantaneous angular velocity. Therefore

$\omega=\frac{\Delta \theta}{\Delta t}$

$45.0 rad/s=\frac{\Delta \theta}{30.0s}$

$\Delta \theta=1350 rad$

Solution for (b)

Tangential speed is the same thing as linear speed.

$v=r\omega$

$v=(0.100m)(45.0 rad/s)$

$v=4.50 m/s$

Discussion

Notice that radian is defined as the length of the arc subtended by an angle divided by the radius. Since “length of arc” and “radius” both have dimensions of length, radian is dimensionless. Therefore when multiplying meter by radian per second (m.rad/s), as we did above, we can drop radian, and the result is simply m/s.

Video Example – Angular and linear speed of children on Merry-Go-Round

rotational kinetic energy and moment of inertia

Any moving object has kinetic energy. We know how to calculate this for a body undergoing translational motion, but how about for a rigid body undergoing rotation? This might seem complicated because each point on the rigid body has a different linear velocity. However, we can make use of angular velocity—which is the same for the entire rigid body—to express the kinetic energy for a rotating object. Consider a wind turbine rotating with an angular velocity ω as shown in Figure 14.6. To find the kinetic energy of one blade of the turbine, we can divide the blade into small segments, each with a mass m_i located at a distance r_i from the rotation axis. Each piece has a linear speed v_i and kinetic energy KE_i=(1/2)m_iv_i². The kinetic energy of the whole blade is the sum of the kinetic energy of all these small pieces making up the blade.

$KE=\sum {\frac{1}{2}m_i {v_i}^2}$

Now, let’s replace v_i with r_iω

$KE=\sum {\frac{1}{2}m_i ({r_i \omega})^2}$

$KE=\frac{1}{2} \omega^2 \sum {m_i {r_i }^2}$

The quantity $\sum {m_i {r_i }^2}$ is called moment of inertia and is represented with letter I and has units of kgm² .

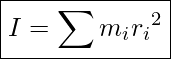$\boxed{I=\sum {m_i {r_i }^2}}$ Moment Of Inertia

Putting it all together, we get the following expression for the rotational kinetic energy.

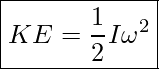$\boxed{KE=\frac{1}{2} I \omega^2}$ Rotational Kinetic Energy

This expression is very similar to the expression for translational kinetic energy, $KE=\frac{1}{2} mv^2$ . The only difference is that instead of mass we have moment of inertia, and instead of linear velocity, we use angular velocity. We already explained why it makes sense to use angular velocity instead of linear velocity when we deal with rotation. Now let’s explore the meaning and significance of the moment of inertia.

Moment of Inertia

Comparing the expressions for translational kinetic energy and rotational kinetic energy, we see that mass is replaced with moment of inertia. In fact, moment of inertia for rotation is the same thing as mass for translational motion. In UNIT 7 we introduced inertia as being resistance against change in motion, and mass as a measure of inertia. Similarly, we can define the moment of inertia as a measure of resistance against change in rotational motion. It is interesting to see how the moment of inertia varies with r, the distance to the axis of rotation. Rigid bodies and systems of particles with more mass concentrated at a greater distance from the axis of rotation have greater moments of inertia than bodies and systems of the same mass but concentrated near the axis of rotation. In this way, we can see that a hollow cylinder has more rotational inertia than a solid cylinder of the same mass when rotating about an axis through the center.

Example 14.2 – Moment of Inertia of a System of Particles

2 small washers are spaced 20 cm apart on a rod of negligible mass. The mass of each washer is 50 g. The rod rotates about an axis midway between the two washers with an angular speed of 50 rpm, as shown in Figure 14.7(a).

(a) What is the moment of inertia of the system shown in Figure 14.7(a)?

(b) If the two washers are moved 20cm from the axis of rotation as shown in Figure 14.7(b), what is the new moment of inertia of the system?

(c) What is the kinetic energy of the system in each case?

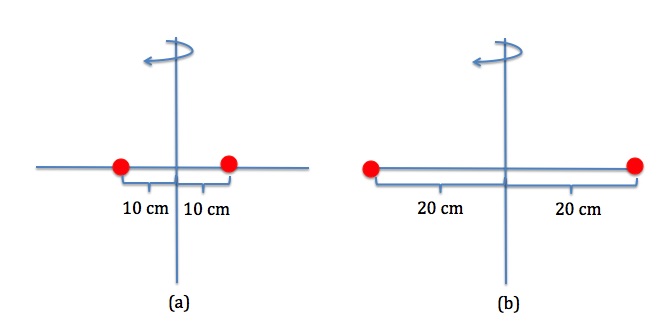
Solution to (a)

Moment of inertia of a system of particles is given by

$I=\sum {m_i {r_i }^2}$

$I=(0.050kg)(0.10m)^2 +(0.050kg)(0.10m)^2$

$I=0.0010 kgm^2$

Solution for (b)

Same reasoning as (a)

$I=\sum {m_i {r_i }^2}$

$I=(0.050kg)(0.20m)^2 +(0.050kg)(0.20m)^2$

$I=0.0040 kgm^2$

Solution for (c)

Rotational kinetic energy is $KE=\frac{1}{2} I \omega^2$ . For the units to work out, I must be in kgm² and ω has to be in rad/s.

Since 1revolution is equal to 2π radian

$50\frac{rev}{min} \times \frac{2\pi rad}{1 rev} \times \frac{1min}{60s}=5.2rad/s$

Kinetic energy for configuration shown in Figure 14.7 (a)

$KE=\frac{1}{2} I \omega^2$

$KE=\frac{1}{2} (0.0010kgm^2)(5.2rad/s)^2$

$KE=0.014J$

Kinetic energy for configuration shown in Figure 14.7 (b)

$KE=\frac{1}{2} I \omega^2$

$KE=\frac{1}{2} (0.0040kgm^2)(5.2rad/s)^2$

$KE=0.054J$

Discussion

Since the masses are farther away from the axis of rotation in (b), the system has a greater moment of inertia. This means it is more difficult to speed up or slow down the rotation of the system in (b) compared to the system in (a).

Video Example – Kinetic energy of a dumbbell

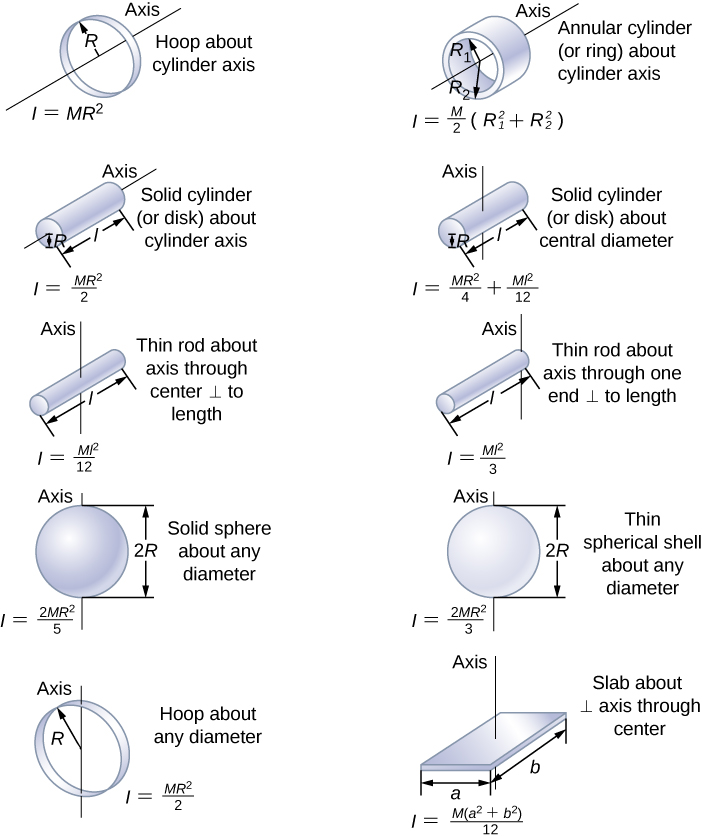
As demonstrated in Example 14.2, the moment of inertia of a system of discrete particles is given by $I=\sum {m_i {r_i }^2}$ . Calculating the moment of inertia of solid objects, such as a sphere or a cylinder, requires calculus. The results of these calculations for some common shape objects are given in Table 14.1

Example 14.3 – Calculating Helicopter’s Energies

A typical small rescue helicopter has four blades: Each is 4.00 m long and has a mass of 50.0 kg (Figure 14.8). The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg.

(a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm.

(b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades.

Solution for (a)

Since rotational kinetic energy is $KE_{rotation}=\frac{1}{2} I \omega^2$ , we need to find the moment of inertia, I, of the blades.

Since each blade can be treated as a thin rod rotating about an axis perpendicular to its length at one end, according to Table 14.1, its moment of inertia is

$I=\frac{1}{3}ML^2$

$I=\frac{1}{3}(50.0kg)(4.00m)^2$

$I=267kgm^2$

Now, we need to change the units of angular speed from rpm (rev/min) to rad/s.

$300\frac{rev}{min} \times \frac{2\pi rad}{1 rev} \times \frac{1min}{60s}=31.4rad/s$

The overall kinetic energy of all four blades is

$KE_{rotation}=4 \times (\frac{1}{2} I \omega^2)$

$KE_{rotation}=4 \times (\frac{1}{2} (267kgm^2)(31.4rad/s)^2]$

$KE_{rotation}=5.25 \times 10^5 J$

Solution for (b)

The translational kinetic energy of the helicopter is

$KE_{translation}=\frac{1}{2} mv^2$

$KE_{translation}=\frac{1}{2} (1000kg)(20.0m/s)^2$

$KE_{translation}=2.00 \times 10^5 J$

To compare the translational kinetic energy of the helicopter with the rotational kinetic energy of the blades we can find the ratio of the two.

$\frac{KE_{rotation}}{KE_{translation}} =\frac{5.25 \times 10^5 J}{2.00 \times 10^5 J}$

$\frac{KE_{rotation}}{KE_{translation}}=2.63$

Discussion

This means most of the kinetic energy of the helicopter is in the spinning blades.

Video Example – Work to rotate a Merry-Go-Round

Table 14.1 provides the formula for calculating the moment of inertia of different shape solid objects when they are rotating about an axis that goes through the center of mass. We can use the moment of inertia about an axis that goes through the center of mass along with the parallel axis theorem to determine the moment of inertia relative to any rotation axis that is parallel to the axis that goes through the center of mass. The parallel axis theorem is

$\boxed{I=I_{cm}+Mh^2}$ parallel axis theorem

Where I_cmis the moment of inertia relative to an axis that goes through the center of mass, M is the mass of the object, and h is the distance between the two parallel axes.

Example 14.4

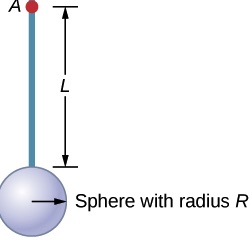
Find the moment of inertia of the rod and solid sphere combination about an axis that goes through point A into the screen as shown below. The rod has a length of 0.50m and a mass of 2.0 kg. The radius of the sphere is 20 cm and has a mass of 1.0 kg.

Solution

The moment of inertia of the system is the sum of the moment of inertia of the rod and the moment of inertia of the sphere. Notice that the moment of inertia of the rod relative to an axis that goes through one end and is perpendicular to the rod is given in table 14.1. But even if we didn’t have this information, we could have derived this formula by using the moment of inertia about an axis that goes through the center of mass and the parallel axis theorem, as follows.

$I_A=I_{cm}+Mh^2$

$I_A=\frac{1}{12}ML^2+Mh^2$

Since the distance between the two parallel axes is one-half the length of the rod

$I_A=\frac{1}{12}ML^2+M(\frac{L}{2})^2$

$I_A=\frac{1}{3}ML^2$ for the rod

This is the same result listed in Table 14.1.

Now we can use the parallel axis theorem one more time to find the moment of inertia of the sphere rotating about an axis through point A.

$I_A=I_{cm}+Mh^2$

$I_A=\frac{2}{5}MR^2+Mh^2$

The distance between the two parallel axes, h, is R+L.

$I_A=\frac{2}{5}MR^2+M(R+L)^2$ for the sphere

Now we can calculate the overall moment of inertia of the system

$I_{system}=I_{rod} + I_{sphere}$

$I_{system}=\frac{1}{3}M_{rod}L^2 + \frac{2}{5}M_{sphere}R^2+M_{sphere}(R+L)^2$

$I_{system}=\frac{1}{3}(2.0kg)(0.50m)^2 + \frac{2}{5}(1.0kg)(0.20cm)^2+(1.0kg)(0.20m+0.50m)^2$

$I_{system}=0.67kgm^2$

Rolling without slipping

In general, when an object rotates while at the same time its center of mass moves forward, the two motions, rotation, and translation are independent of one another. For example, when there is not enough friction, the wheels of a car can spin in place and not move forward at all, or move forward just a little bit. But under the right conditions, we end up with a special situation where the object rolls without slipping. In this section, we will look at rolling without slipping more closely.

When an object, let’s say a disk as shown in Figure 14.10, rolls without slipping, the distance that the center of mass moves forward in a time interval, Δt, is exactly equal to the length of the arc subtended by the rotation angle, θ. This distance is marked with S in Figure 14.10. This means that the linear speed of a point on the edge of the disk is equal to the speed of the center of mass, v_cm.

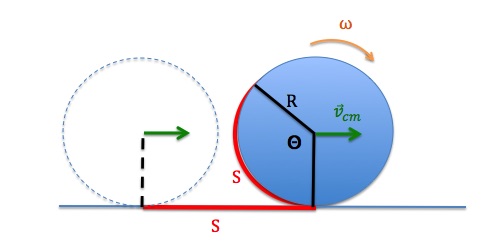
As we saw earlier in this unit, the linear speed of a point on a rotating object and the angular speed are related according to $v=r\omega$ . Therefore, when there is rolling without slipping the translational motion of the center of mass and the rotational motion are related.

$\boxed{v_{cm}=R\omega}$ Rolling without slipping

where v_cm is the speed of the center of mass, R is the radius of the object, and ω is its rotational angular speed.

Example 14.5

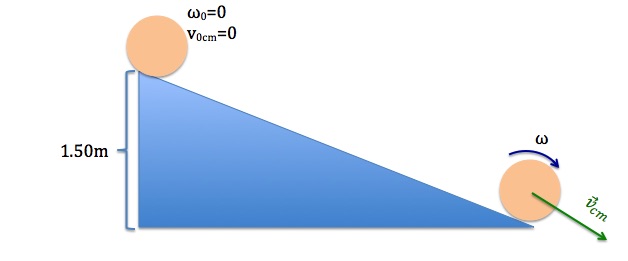
A ball starts from rest and rolls down an inclined plane from a height of 1.50m without slipping. Find the speed of the ball at the bottom of the hill. Treat the ball as a spherical shell.

Solution

In the past, in problems like this, we treated the object as a point mass, and we never had to deal with rotation. One way to solve this problem and include rotation is to use the work-energy principle. Notice that even though there is friction between the ball and the incline (otherwise the ball would slide down and not roll at all), this friction force is not doing any work because the point of contact between the ball and the incline where the friction force acts is continuously moving up as the ball rotates and is not sliding along the incline. The non-conservative forces on the ball are the friction force, and the normal force, both applied by the incline. Since neither force does work, we can apply the principle of conservation of energy as the ball goes from the state (1) which is the top of the incline to state (2) which is the bottom of the incline. Let’s set y=0 at the bottom of the incline.

$State(1)$ $\Rightarrow$ $State(2)$

$KE_1+U_1 =KE_2 + U_2$

$0 + mgy =\frac{1}{2}mv_{cm}^2 +\frac{1}{2}I\omega^2+0$

Since the ball is rolling without slipping

$\omega=\frac{v_{cm}}{R}$

And the ball is like a hollow spherical shell. Look up the moment of inertia of a spherical shell in Table 14.1.

$I=\frac{2}{3}mR^2$

Putting it all together we get

$mgy =\frac{1}{2}mv_{cm}^2 +\frac{1}{2}(\frac{2}{3}mR^2)(\frac{v_{cm}}{R})^2$

$gy =\frac{5}{6}v_{cm}^2$

$(9.8m/s^2)(1.50m) =\frac{5}{6}v_{cm}^2$

$v_{cm}=4.2m/s$

Video Example – Race between a hoop, a solid cylinder, and a solid sphere

Video Example – Ball rolling around a loop

Attributions

This chapter contains material taken from Openstax College Physics-Rotational Motion and Angular Momentum, and Openstax University Physics Volume 1 – Fixed Axis Rotation and is used under a CC BY 4.0 license. Download these books for free at Openstax

To see what was changed, refer to the List of Changes.

problems

The distance between the Earth and the Sun is 1.52×10¹¹m, the radius of the Earth is 6.371×10⁶m, and the mass of the Earth is 5.972×10²⁴kg.
1. Calculate the angular and linear speed of the Earth as it revolves around the Sun in rad/s and m/s respectively.
2. Calculate the angular and linear speed of a point on the surface of the earth as it rotates about its axis in rad/s and m/s respectively.
3. Calculate the rotational kinetic energy of the Earth as it revolves around the Sun.
4. Calculate the rotational kinetic energy of the Earth as it rotates about its axis.
[openstax univ. phys. vol. 1 – 10.32]A compact disc rotates at 500 rev/min. If the diameter of the disc is 120 mm.
1. What is the linear (or tangential) speed of a point at the edge of the disc?
2. What is the linear (or tangential speed) of a point halfway to the center of the disc?
[openstax univ. phys. vol. 1 – 10.56] Calculate the rotational kinetic energy of a 12.0-kg motorcycle wheel if its angular velocity is 120 rad/s and its inner radius is 0.280 m and outer radius 0.330 m.
[openstax univ. phys. vol. 1 – 10.57] A baseball pitcher throws the ball in a motion where there is a rotation of the forearm about the elbow joint as well as other movements. If the linear velocity of the ball relative to the elbow joint is 20.0 m/s at a distance of 0.480m from the joint and the moment of inertia of the forearm is 0.500kgm², what is the rotational kinetic energy of the forearm?
[openstax univ. phys. vol. 1 – 10.65] Using the parallel axis theorem, what is the moment of inertia of the rod of mass m about the axis shown below?
[openstax univ. phys. vol. 1 – 11.28] A bowling ball rolls up a ramp 0.500 m high without slipping. The ball has an initial velocity of 3.00 m/s. What is its velocity at the top of the ramp?
[openstax univ. phys. vol. 1 – 11.29&11.30] A 40.0-kg solid cylinder and a 40.0-kg solid sphere are rolling across a horizontal surface at a speed of 6.00 m/s.
1. How much work is required to stop the solid cylinder?
2. How much work would it require to stop the sphere?
[openstax univ. phys. vol. 1 – 10.47] A man stands on a merry-go-round that is rotating at 2.50 rad/s. If the coefficient of static friction between the man’s shoes and the merry-go-round is μ_s=0.500 how far from the axis of rotation can he stand without sliding?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Rotational motion and angular velocity

rotation angle

Angular velocity

rotational kinetic energy and moment of inertia

Moment of Inertia

Rolling without slipping

Attributions

problems

License

Share This Book