Unit 5 – Projectile Motion

Beta Keramati

Kinematics – Motion in Two Dimensions

Last Update: 9/19/2023

kinematics of projectile motion

Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, such as that of a football or other object for which air resistance is negligible. The following simulation shows a ball being projected below horizontal, horizontally, and at angles above the horizontal.

The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. This choice of axes is the most sensible because the acceleration due to gravity is vertical—thus, there will be no acceleration along the horizontal axis when air resistance is negligible. As is customary, we call the horizontal axis the x-axis and the vertical axis the y-axis.

The following steps are then used to analyze projectile motion:

Step 1. Resolve or break the motion into horizontal and vertical components along the x- and y-axes.

Step 2. Treat the motion as two independent one-dimensional motions, one horizontal with constant velocity and the other vertical with constant acceleration.

The kinematic equations for horizontal and vertical motion take the following forms:

Horizontal Motion – The x-component of velocity is constant (V_x = V_0x = constant)

$x = v_{0x} t + x_0$

Vertical Motion – Acceleration is due to gravity and therefore constant (a_y = 9.8m/s² ↓)

$y=\frac{1}{2}a_y t^2 + v_{0y} t + y_0$

$v_y = a_y t + v_{0y}$

$v^2_y - v^2_{0y} = 2 a_y \Delta y$

$\bar v_y = \frac{v_{0y} + v_y}{2}$

Step 3. Solve for the unknowns in the two separate motions—one horizontal and one vertical. Note that the only common variable between the motions is time, t.

Step 4. Recombine the two motions to find the total displacement and the total velocity at any point along the trajectory.

Figure 5.1 shows how we analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. The horizontal motion is simple because the horizontal component of the velocity does not change. In the vertical direction, the acceleration is due to gravity and therefore constant and downward at all times. This means that while the object is moving up, its velocity in the y-direction decreases at a rate of 9.8m/s every second, and while it is moving down, this velocity increases at a rate of 9.8m/s every second.

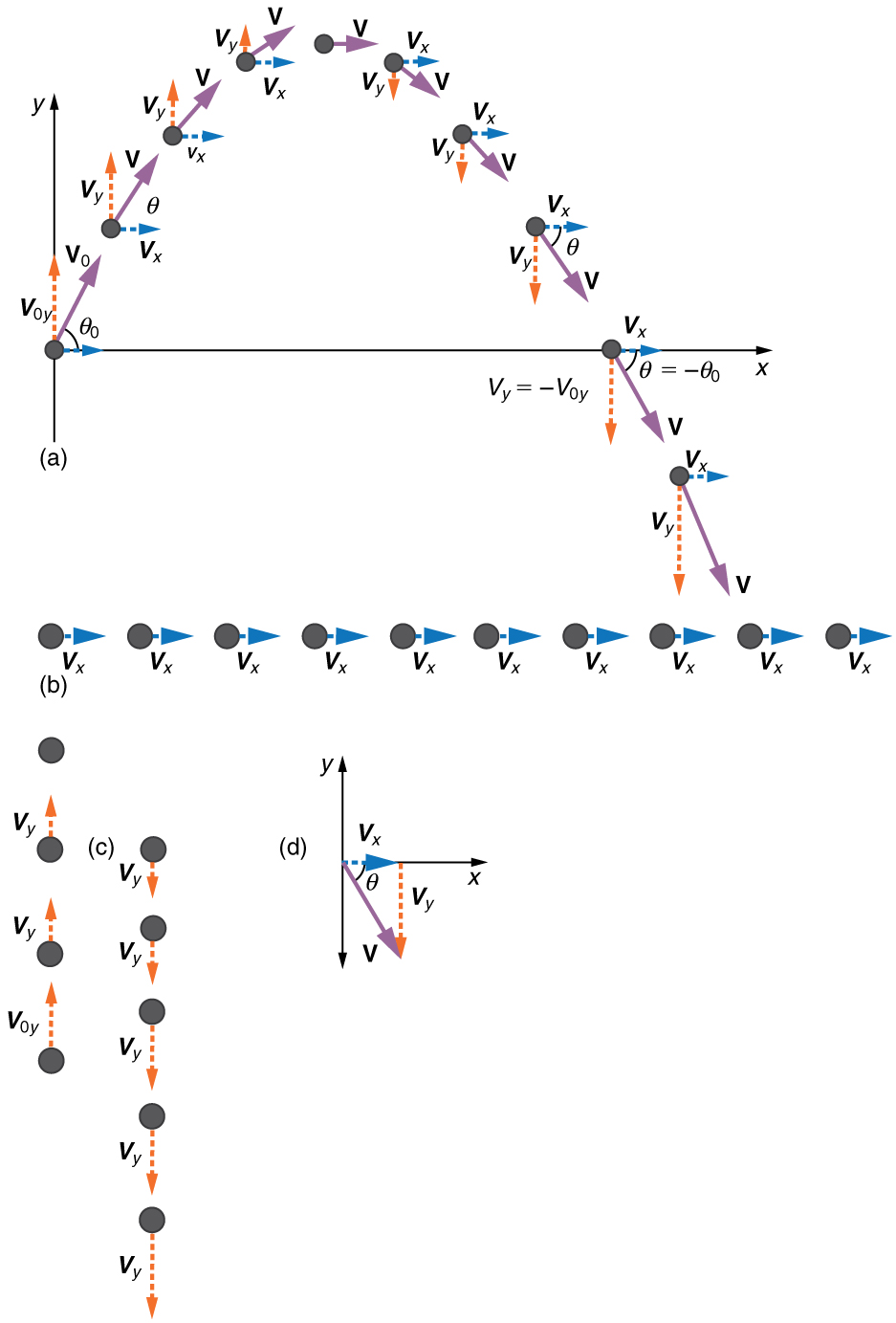
In part a the figure shows projectile motion of a ball with initial velocity of v zero at an angle of theta zero with the horizontal x axis. The horizontal component v x and the vertical component v y at various positions of ball in the projectile path is shown. In part b only the horizontal velocity component v sub x is shown whose magnitude is constant at various positions in the path. In part c only vertical velocity component v sub y is shown. The vertical velocity component v sub y is upwards till it reaches the maximum point and then its direction changes to downwards. In part d resultant v of horizontal velocity component v sub x and downward vertical velocity component v sub y is found which makes an angle theta with the horizontal x axis. The direction of resultant velocity v is towards south east. — Figure 5.1

It is important to set up a coordinate system when analyzing projectile motion. One part of defining the coordinate system is to define an origin for the x and y positions. Often, it is convenient to choose the initial position of the object as the origin such that x₀=0 and y₀=0. It is also important to define the positive and negative directions in the x and y directions. Typically, we define the positive vertical direction as upwards, and the positive horizontal direction is usually the direction of the object’s motion. When this is the case, the vertical acceleration, acceleration due to gravity, takes a negative value (since it is directed downwards towards the center of the Earth). However, it is occasionally useful to define the coordinates differently. For example, if you are analyzing the motion of a ball thrown downwards from the top of a cliff, it may make sense to define the positive direction downwards since the motion of the ball is solely in the downwards direction. If this is the case, the vertical acceleration, acceleration due to gravity, takes a positive value.

A fundamental concept to remember when analyzing projectile motion is that the velocities in the horizontal and vertical directions are completely independent of one another. In other words, the horizontal and vertical parts of the motion are two independent motions that occur at the same time. One way to demonstrate this is to compare the time in the air of a bullet that is dropped from a certain height with the time in the air of a bullet that is fired horizontally from the same height. Since the fired bullet leaves the gun horizontally, its initial velocity in the vertical direction is zero, just like the initial velocity of the dropped bullet. If the vertical and horizontal motions are truly independent, then we should expect both bullets to hit the ground at the same time. Do they? Let’s watch this Myth Busters video and find out.

Notice that even with air resistance it takes practically the same amount of time for the two bullets to reach the ground. In this book, we will ignore the effect of air resistance on all projectile motions unless stated explicitly otherwise.

Example 5.1 – A Fireworks Projectile Explodes High And Away

During a fireworks display, a shell is shot into the air with an initial speed of 70.0 m/s at an angle of 75.0º above the horizontal, as illustrated below. The fuse is timed to ignite the shell just as it reaches its highest point above the ground.

(a) Calculate the height at which the shell explodes.

(b) How much time passed between the launch of the shell and the explosion?

(c) What is the horizontal displacement of the shell when it explodes?

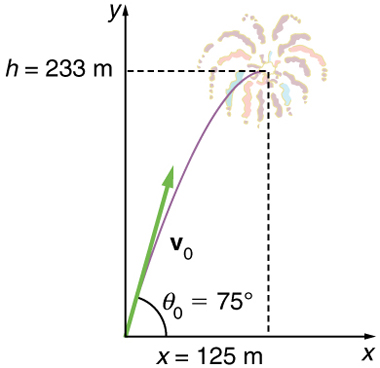
The x y graph shows the trajectory of fireworks shell. The initial velocity of the shell v zero is at angle theta zero equal to seventy five degrees with the horizontal x axis. The fuse is set to explode the shell at the highest point of the trajectory which is at a height h equal to two hundred thirty three meters and at a horizontal distance x equal to one hundred twenty five meters from the origin. — Figure 5.2

Strategy

Because air resistance is negligible for the unexploded shell, the analysis method outlined above can be used. The motion can be broken into horizontal and vertical motions in which a_x=0 and a_y=9.8m/s² ↓. We can then define x₀=0 and y₀=0 at the starting point and solve for the desired quantities.

Solution for (a)

By “height”, we mean the altitude or vertical position y above the starting point. The highest point in any trajectory, called the apex, is reached when v_y=0. If we take the initial position to be the starting point and the final position to be the apex, we know the initial and final velocities as well as the initial position, and we can use the following equation to find the final position y:

$v^2_y - v^2_{0y} = 2 a_y \Delta y$

Let’s take “up” to be the positive direction.

Now we must find v_0y, the component of the initial velocity in the y-direction.

$sin \theta_0 = \frac{v_{0y}}{v_0}$

$v_{0y}= v_0 sin \theta_0$

$v_{0y}= (70.0m/s) sin(75^\circ)$

$v_{0y}= 67.6 m/s$

Since we also know y₀ =0 and v_y=0, and a_y=-9.8m/s², we can now solve for y.

$(0 m/s)^2 - (67.6 m/s)^2 = 2 (-9.8 m/s^2) (y-0)$

$y=233 m$

Discussion for (a)

Note that because up is positive, the initial velocity is positive, as is the maximum height, but the acceleration due to gravity is negative. Note also that the maximum height depends only on the vertical component of the initial velocity so that any projectile with a 67.6 m/s initial vertical component of velocity will reach a maximum height of 233 m (neglecting air resistance). The numbers in this example are reasonable for large fireworks displays, the shells of which do reach such heights before exploding. In practice, air resistance is not completely negligible, and so the initial velocity would have to be somewhat larger than that given to reach the same height.

Solution for (b)

As in many physics problems, there is more than one way to solve for the time to the highest point. In this case, the easiest method is to use

$v_y = a_y t + v_{0y}$

Since at the top, v_y=0

$0 = (-9.8m/s^2) t + 67.6 m/s$

$t=6.90 s$

Discussion for (b)

This time is also reasonable for large fireworks. When you are able to see the launch of fireworks, you will notice several seconds pass before the shell explodes.

Solution for (c)

Because air resistance is negligible, the horizontal velocity is constant, as discussed above. We can find the horizontal velocity by calculating the x-component of the initial velocity.

$cos \theta_0 = \frac{v_{0x}}{v_0}$

$v_{0x}= v_0 cos \theta_0$

$v_{0x}= (70.0m/s) cos(75^\circ)$

$v_{0x}= 18.1 m/s$

We also know x₀=0, and now we can solve for the horizontal displacement.

$x = v_{0x} t + x_0$

$x = (18.1 m/s)(6.90 s) + 0$

$x = 125 m$

Discussion for (c)

The horizontal motion is a motion with constant velocity in the absence of air resistance. The horizontal displacement found here could be useful in keeping the fireworks fragments from falling on spectators. Once the shell explodes, air resistance has a major effect, and many fragments will land directly below.

Video Example – Ball kicked from the ground level

Example 5.2 – Calculating Projectile Motion: Hot Rock Projectile

Kilauea in Hawaii is the world’s most continuously active volcano. Very active volcanoes characteristically eject red-hot rocks and lava rather than smoke and ash. Suppose a large rock is ejected from the volcano with a speed of 25.0 m/s and at an angle 35.0º above the horizontal, as shown below. The rock strikes the side of the volcano at an altitude 20.0 m lower than its starting point.

(a) Calculate the time it takes the rock to follow this path.

(b) What are the magnitude and direction of the rock’s velocity at impact?

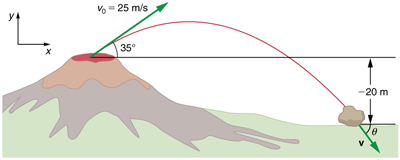
The trajectory of a rock ejected from a volcano is shown. The initial velocity of rock v zero is equal to twenty five meters per second and it makes an angle of thirty five degrees with the horizontal x axis. The figure shows rock falling down a height of twenty meters below the volcano level. The velocity at this point is v which makes an angle of theta with horizontal x axis. The direction of v is south east. — Figure 5.3

Strategy

Again, resolving this two-dimensional motion into two independent one-dimensional motions will allow us to solve for the desired quantities. The time a projectile is in the air is governed by its vertical motion alone. We will solve for t first. While the rock is rising and falling vertically, the horizontal motion continues at a constant velocity. This example asks for the final velocity. Thus, the vertical and horizontal results will be recombined to obtain the magnitude and direction of the velocity at the final time t determined in the first part of the example.

Solution for (a)

While the rock is in the air, it rises and then falls to a final position 20.0 m lower than its starting altitude. We can find the time for this by using

$y=\frac{1}{2}a_y t^2 + v_{0y} t + y_0$

If we take the initial position y₀=0, then the final position is y =-20.0m. Now the initial vertical velocity is the y- component of the initial velocity.

$sin \theta_0 = \frac{v_{0y}}{v_0}$

$v_{0y}= (25.0m/s) sin(35.0^\circ)$

$v_{0y}= 14.3 m/s$

Substituting known values yields

$-20.0 m=\frac{1}{2}(-9.8 m/s^2) t^2 + (14.3 m/s)t + 0$

Rearranging terms gives a quadratic equation in t.

$(4.90 m/s^2)t^2 -(14.3 m/s)t -(20.0 m)=0$

This equation is in the form of $a t^2 +bt +c=0$ which is solved by using the quadratic formula $t=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$

Applying the quadratic formula yields:

$t=\frac{14.3 \pm \sqrt{(14.3)^2+4(4.90)(20.0)}}{2(4.90)}$

$t=3.96s$ and $t=-1.03s$

The negative value of time implies an event before the start of motion, and so we discard it. Thus, $t=3.96s$

Discussion for (a)

The time for projectile motion is completely determined by the vertical motion. So any projectile that has an initial vertical velocity of 14.3 m/s and lands 20.0 m below its starting altitude will spend 3.96 s in the air.

Solution for (b)

From the information now in hand, we can find the horizontal and vertical components of the final velocity, v_x and v_y, and combine them to find the total velocity and the angle it makes with the horizontal. Of course, v_x is constant so we can solve for it at any horizontal location. In this case, we chose the starting point since we know both the initial velocity and initial angle. Therefore:

$cos \theta_0 = \frac{v_{0x}}{v_0}$

$v_{0x}= (25.0m/s) cos(35.0^\circ)$

$v=v_{0x}= 20.5 m/s$

The final vertical velocity can be calculated by the following equation:

$v_y = a_y t + v_{0y}$

$v_y = (-9.8 m/s^2)(3.96 s) + 14.3 m/s$

$v_y = -24.5 m/s$

To find the magnitude of the final velocity from its components, we can use the Pythagorean theorem, which gives

$v=\sqrt{(20.5 m/s)^2 + (-24.5 m/s)^2}$

$v=31.9 m/s$

The direction of the final velocity is determined by calculating the angle the velocity makes with the horizontal, Θ.

$tan \theta =\frac{v_y}{v_x}$

$\theta =tan^{-1}(\frac {-24.5}{20.5})$

$\theta =-50.1^\circ$

Therefore, the final velocity at the moment of impact is

$\vec v = 31.9 m/s @ -50.1^\circ$

Discussion for (b)

The negative angle means that the velocity is below the horizontal. This result is consistent with the fact that the final vertical velocity is negative and hence downward—as you would expect because the final altitude is 20.0 m lower than the initial altitude.

Video Example – Object released from a diving airplane

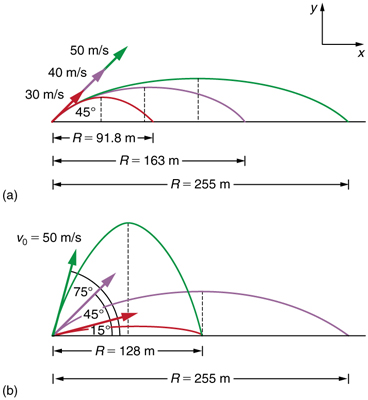
How does the initial velocity of a projectile affect its range? Obviously, the greater the initial speed, the greater the range, as shown in Figure 5.2(a). The initial angle θ also has a dramatic effect on the range, as illustrated in Figure 5.2(b). For a fixed initial speed, such as might be produced by a cannon, the maximum range is obtained with θ0=45º size. This is true only for conditions neglecting air resistance. Interestingly, for every initial angle except 45º, there are two angles that give the same range—the sum of those angles is 90º size.

Part a of the figure shows three different trajectories of projectiles on level ground. In each case the projectiles makes an angle of forty five degrees with the horizontal axis. The first projectile of initial velocity thirty meters per second travels a horizontal distance of R equal to ninety one point eight meters. The second projectile of initial velocity forty meters per second travels a horizontal distance of R equal to one hundred sixty three meters. The third projectile of initial velocity fifty meters per second travels a horizontal distance of R equal to two hundred fifty five meters. — Figure 5.4

Example 5.3

A tennis player wins a match at Arthur Ashe stadium and hits a ball into the stands at 30.0 m/s and at an angle 45º above the horizontal. On its way down, the ball is caught by a spectator 10.0 m above the point where the ball was hit.

(a) Calculate the time it takes the tennis ball to reach the spectator.

(b) What are the magnitude and direction of the ball’s velocity at impact?

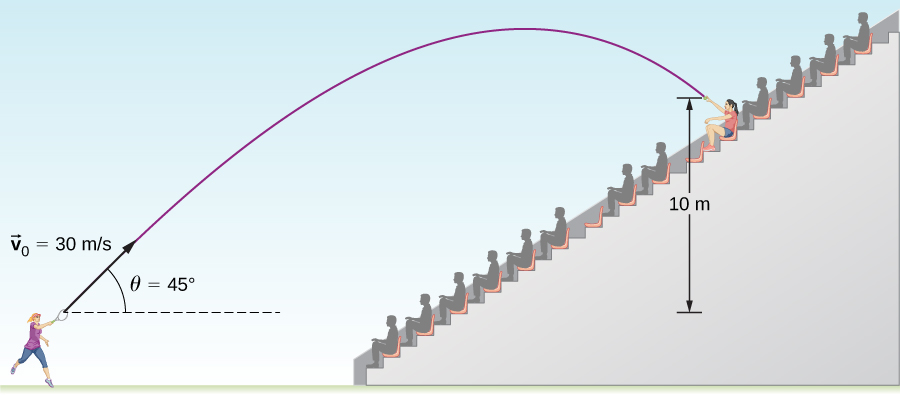
Solution for (a)

The time a projectile is in the air is governed by its vertical motion alone. We need to first find the vertical component of the initial velocity and then use the vertical part of the motion to determine the time it takes the ball to reach a position 10m above its starting point on its way down.

$sin \theta = \frac{v_{0y}}{v_0}$

$v_{0y}= (30.0m/s) sin(45.0^\circ)$

$v_{0y}= 21.2 m/s$

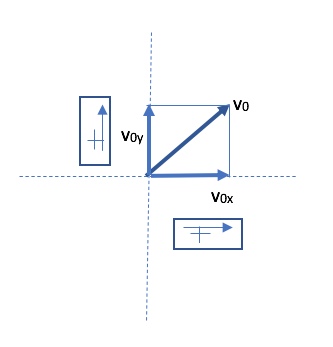
Now we can find the time the ball is in the air by using

$y=\frac{1}{2}a_y t^2 + v_{0y} t + y_0$

We take the origin to be where the ball is released.

$10.0m=\frac{1}{2}(-9.8m/s^2) t^2 + 21.2m/s t + 0$

Rearranging this we get a quadratic equation.

$(4.9m/s^2)t^2 - (21.2m/s)t + 10.0m=0$

The solutions are: t=3.79s, and t=0.54s. The smaller value, t-0.54s is the time it takes the ball to reach a height of 10.0m on its way up, and the longer time, t=3.79s is the time it takes to reach the same height on its way down. Notice that the time for projectile motion is determined completely by the vertical motion. Thus, any projectile that has an initial vertical velocity of 21.2 m/s and lands 10.0 m below its starting altitude spends 3.79 s in the air.

Solution for (b)

The ball’s horizontal component of the velocity does not change. We can determine this component by using the initial velocity.

$cos \theta = \frac{v_{0x}}{v_0}$

$v_{0x}= (30.0m/s) cos(45.0^\circ)$

$v=v_{0x}= 21.2 m/s$

Now let’s find the vertical component of the velocity at the instant the ball is caught.

$v_y = a_y t + v_{0y}$

$v_y = (-9.8 m/s^2)(3.79 s) + 21.2 m/s$

$v_y = -15.9 m/s$

So, at the moment the ball is caught, its velocity is $\vec v=21/2m/s \hat i -15.9m/s \hat j$ .

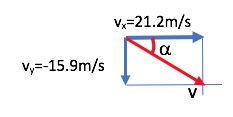
Now let’s use the Pythagorean theorem to find the magnitude of the velocity.

$v=\sqrt{(21.2 m/s)^2 + (-15.9 m/s)^2}$

$v=26.5 m/s$

To find the direction, we calculate the angle between the velocity vector and the horizontal line, θ.

$tan \alpha =\frac{v_y}{v_x}$

$\alpha =tan^{-1}(\frac {-15.9}{21.2})$

$\alpha =-36.9^\circ$

So, at the moment the ball is caught, its velocity is $\vec v = 26.5 m/s @ -36.9^\circ$

Attributions

This chapter contains material taken from Openstax College Physics-Kinematics in Two Dimensions by Openstax and is used under a CC BY 4.0 license. Download this book for free at Openstax-College Physics

To see what was changed, refer to the List of Changes.

problems

An object is projected with an initial velocity v₀ from a height of 10.0m from the ground. Determine how long the object is in the air, the velocity with which it strikes the ground (magnitude and direction), and the horizontal distance traveled when it lands for the following cases.
1. The initial velocity is horizontal and has a magnitude of 5.00m/s.
2. The initial velocity is 5.00m/s at 30.0^° above the horizontal.
3. The initial velocity is 5.00m/s at 30.0^° below the horizontal.
[openstax univ. phys. vol. 1 – 4.39] A projectile is launched at an angle of 30º and lands 20.0 s later at the same height as it was launched.
1. What is the initial speed of the projectile?
2. What is the maximum altitude?
3. What is the horizontal distance traveled?
[openstax univ. phys. vol. 1 – 4.40] A basketball player shoots toward a basket 6.10 m away and 3.0 0m above the floor. If the ball is released 1.80 m above the floor at an angle of 60.0º above the horizontal, what must the initial speed be if it were to go through the basket?
[openstax univ. phys. vol. 1 – 4.41] At a particular instant, a hot air balloon is 100 m in the air and descending at a constant speed of 2.00 m/s. At this exact instant, a girl throws a ball horizontally, relative to herself, with an initial speed of 15.0 m/s. When she lands, where will she find the ball?
[openstax univ. phys. vol. 1 – 4.45] A rock is thrown off a cliff with a velocity of 30.0m/s at an angle of 53.0º with respect to the horizontal. The cliff is 100 m high.
1. How high above the edge of the cliff does the rock rise?
2. How far has it moved horizontally when it is at maximum altitude?
3. How long after the release does it hit the ground?
4. What is the horizontal distance traveled by the rock when it lands?
5. What are the horizontal and vertical positions of the rock relative to the edge of the cliff at t = 4.00 s?
[openstax univ. phys. vol. 1 – 4.46] Trying to escape his pursuers, a secret agent skis off a slope inclined at 30.0º below the horizontal at 60.0 km/h. To survive and land on the snow 100 m below, he must clear a gorge 60.0 m wide. Does he make it? Ignore air resistance.
[openstax univ. phys. vol. 1 – 4.55] A soccer goal is 2.44 m high. A player kicks the ball at a distance of 10.0 m from the goal at an angle of 25.0º. The ball hits the crossbar at the top of the goal. What is the initial speed of the soccer ball?
[openstax univ. phys. vol. 1 – 4.57] In 1999, Robbie Knievel was the first to jump the Grand Canyon on a motorcycle. At a narrow part of the canyon (69.0 m wide) and traveling 35.8 m/s off the takeoff ramp, he reached the other side. What was his launch angle? He landed at the same height that he left the ramp.
[Jeffrey Schnick – SAC 110] A person throws a rock directly forward over flat level ground. The rock leaves the thrower’s hand at a height of 1.67 m above ground level with a velocity of 14.2 m/s directed along the horizontal. How far forward does the rock go before it hits the ground?
[Jeffrey Schnick – SAC 110] A person hits a golf ball over flat level ground directly toward a wall which is facing the golfer. The ball does hit the wall. The ball leaves the golf club at ground level from a point that is 52.0 m from the wall with a velocity of 33.0 m/s at an angle of 29.0° above the horizontal. How high up on the wall does the ball hit?
[B. Crowell, B. Shotwell-modified] A baseball pitcher throws a pitch clocked at 33.0 m/s. He throws the ball horizontally.
1. By what amount, d, does the ball drop by the time it reaches home plate, a distance 18.3 m away?
2. What is the magnitude and direction of the velocity of the ball when it is above the home plate?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

kinematics of projectile motion

Attributions

problems

License

Share This Book