Unit 13 – Simple Harmonic Motion

Beta Keramati

Oscillations

Unit 13 – Simple Harmonic Motion

Last Update: 5/23/2025

Description of simple harmonic motion

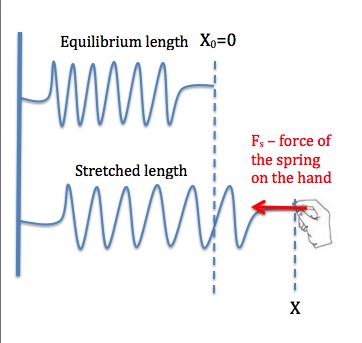
Periodic motion refers to any motion that repeats itself at regular intervals of time. An object undergoing periodic motion returns to its initial position after a fixed duration, known as the period (T). Periodic motion can be observed in a variety of natural and engineered systems. Some examples include the back-and-forth swinging motion of a pendulum, the Earth’s revolutions around the Sun, the vibrations of a guitar string, and the rotations of a Ferris Wheel. A Simple Harmonic Motion (SHM) is a specific type of periodic motion. In a SHM, the force responsible for maintaining the periodic motion of an object is a restoring force that is proportional to the displacement of the object from its equilibrium position. A familiar restoring force is the force applied by a compressed or stretched spring. As we saw in the previous units, when a spring is stretched or compressed, the spring applies a force that is given by Hooke’s Law as

$F_{spring}=-kx$

K is the spring constant and is a measure of the stiffness of the spring. The negative sign indicates that the direction of the force is always opposite to the direction of the displacement of the end of the spring from its equilibrium position. The term “restoring” force is used because the force always tends to restore the spring back to its equilibrium length.

From the examples of the periodic motion mentioned above, only the swinging of a pendulum, and the vibration of a guitar string are governed by a restoring force and are considered to be simple harmonic motions. The parameters used to describe a Simple Harmonic Motion are:

Period – T – time of one oscillation, measured in seconds (s).

Frequency – f – number of oscillations per second, measured in Hertz (Hz). 1Hz=1/s

Amplitude – A – maximum displacement of the object from its equilibrium position, measured in meters.

In this unit, we will examine the simple harmonic motions of a mass attached to a spring and a swinging pendulum.

SHM of a mass-spring system

Consider a block attached to a horizontal spring as shown below. Assume the block and the surface are frictionless. Initially, the spring is at its equilibrium length, and the position of the block is at x=0.

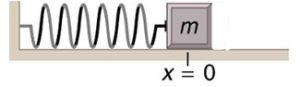
Now, suppose that a person pushes the block to the left to compress the spring and then lets it go. The following figures show the motion of the block and its free body diagram as it oscillates back and forth.

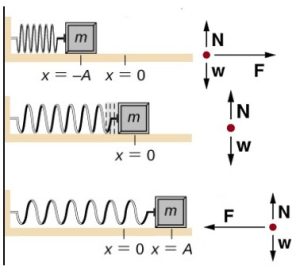
Similarly, an object attached to a vertical spring will also generate a SHM about its equilibrium position, as shown below.

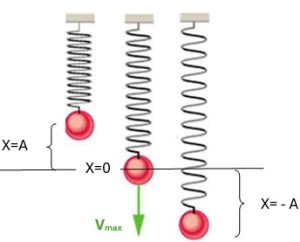
A unique characteristic of a SHM is that the period and frequency of oscillations do not depend on the amplitude. In the case of a mass-spring system, the period and frequency are:

$T=2\pi\sqrt{\frac{m}{k}$ and $f=\frac{1}{2\pi}\sqrt{\frac{k}{m}$

m is the mass of the block and k is the spring constant.

If the oscillations start when the object is farthest away from its equilibrium point (x=A), the equation of motion is a cosine function.

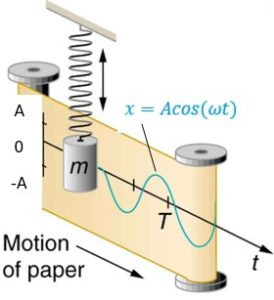
If at $t=0$ , $x=A$ then $x=Acos{\omega t}$ . In this equation $\omega=2\pi f=\frac{2\pi}{T}$

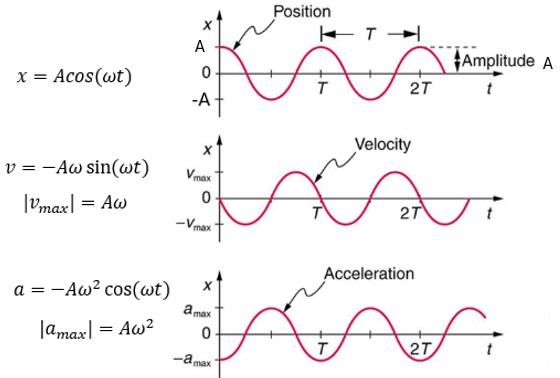
The graphs of position, velocity, and acceleration are shown below.

Energy in a mass-spring system

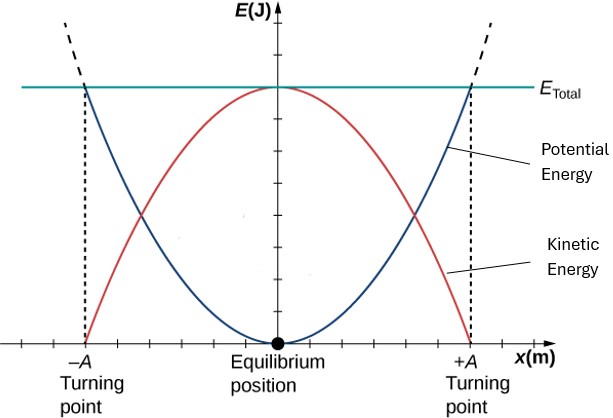
Since the restoring force of a spring is conservative, in the absence of friction, the mechanical energy of an oscillating mass-spring system is conserved. For a horizontal mass-spring system, the mechanical energy consists of the kinetic energy and the elastic potential energy. Conservation of mechanical energy means that the sum of these two energies stays constant as the mass oscillates. Notice that when the mass is farthest away from the equilibrium where x=A, the speed is momentarily zero and all the energy is elastic potential energy. Also, at the instant the mass passes the equilibrium point where x=0, the mass has its maximum speed and all the energy is kinetic. Putting all this together, we get the following result:

$\frac{1}{2}mv^2 +\frac{1}{2}kx^2=\frac{1}{2}mv_{max}^2=\frac{1}{2}kA^2$

At first glance, it appears that in a vertical mass-spring system, we also have to include the change in the gravitational potential energy in our analysis. But, it turns out that if we set x=0 where the mass attached to the spring is at equilibrium, the change in the gravitational potential energy doesn’t affect the result, and the above equation remains valid.

The following is a graphical representation of the conservation of mechanical energy.

Example 13.1

A 2.00kg block is attached to a horizontal spring and placed on a horizontal frictionless surface. The spring constant is 32.0N/m. The block is pulled 0.02m from its equilibrium position and let go. Once released, the block undergoes a SHM between x=-0.02m and x=0.02m.

a) Determine position, velocity, and acceleration as functions of time.

b) What is the mechanical energy of this block-spring system?

c) Find the speed of the block when its position is x=0.01m.

Solution

a) For a SHM, the position as a function of time is given by $x=Acos(\omega t)$ , where A =0.02m is the amplitude and ω=2πf.

$\omega =2 \pi f$ and $f=\frac{1}{2\pi}\sqrt{\frac{k}{m}$

$\omega =2 \pi \frac{1}{2\pi}\sqrt{\frac{k}{m}$

$\omega =\sqrt{\frac{32.0N/m}{2.00kg}$

$\omega =4.00 \frac{1}{s}$

So, the position as a function of time is $x=0.02mcos(4.00 \frac{1}{s} t)$

The velocity as a function of time is $v=-A \omega sin(\omega t)$ . So, in this problem $v=-(0.02m)(4.00 \frac{1}{s} )sin(4.00 \frac{1}{s} t)$

$v=-0.08 \frac{m}{s} sin(\(4.00 \frac{1}{s} t)$

The acceleration as a function of time is $a=-A {\omega}^2 cos(\omega t)$ . So, in this problem $a=-(0.02m)({4.00 \frac{1}{s} })^2 cos(4.00 \frac{1}{s} t)$

$a=-0.32m/s^2cos(4.00 \frac{1}{s} t)$

b) Since there is no friction between the block and the surface, the mechanical energy is conserved.

$\frac{1}{2}mv^2 +\frac{1}{2}kx^2=\frac{1}{2}mv_{max}^2=\frac{1}{2}kA^2$

Mechanical Energy of the block-spring system= $\frac{1}{2}kA^2$

Mechanical Energy of the block-spring system= $\frac{1}{2}(32.0N/m)(0.02m)^2$

Mechanical Energy of the block-spring system= $0.0128J$

c) Using the conservation of energy

$0.0128J=\frac{1}{2}mv^2 +\frac{1}{2}kx^2$

$0.0128J=\frac{1}{2}(2.00kg)v^2 +\frac{1}{2}(32.0N/m)(0.01m)^2$

$v=0.098m/s$ This is the speed of the block when its position is x=0.01m.

SHM of a simple pendulum

A simple pendulum consists of a point mass, sometimes referred to as the pendulum bob, suspended from a light string of negligible mass that swings back and forth with a small angle.

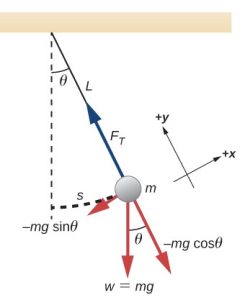
Let’s consider the free body diagram for the point mass and pick the x-y axis parallel and perpendicular to the string, as shown above. Notice that the tension force, F_T cancels one component of the gravitational force, mgcosθ. The only unbalanced force is the other component of the gravitational force, mgsinθ, that acts as a restoring force, always tending to move the pendulum bob toward its equilibrium position. For small angles, the angle expressed in radian is numerically extremely close to the sin of that angle. So, for small angles (θ<15° or θ<0.26 rad) we can safely replace sinθ, with θ(rad). This is called small angle approximation. See the table below.

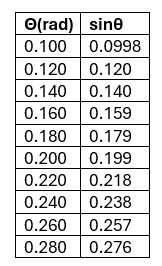
The definition of radian is, $\theta (rad)=\frac{S}{L}$ , where s is the length of the arc subtended by the angle θ, and L is the radius of the circle, which in this case, is the length of the string. Putting all this together we get

Restoring force: $F=mgsin\theta=mg\theta=mg\frac{S}{L}$

This means that the restoring force is directly proportional to s, the distance that the pendulum bob has been displaced from its equilibrium position. Therefore, a swinging pendulum also exhibits a Simple Harmonic Motion. As the case is with any SHM, the period and frequency of oscillations are independent of the amplitude. For a simple pendulum

$T=2\pi\sqrt{\frac{L}{g}$ and $f=\frac{1}{2\pi}\sqrt{\frac{g}{L}$

Example 13.2

What is the acceleration due to gravity in a region where a simple pendulum having a length of 75.00cm has a period of 1.7357s

Solution

We can use the equation mentioned above to solve this problem.

$T=2\pi\sqrt{\frac{L}{g}$

$1.7357s=2\pi\sqrt{\frac{0.7500m}{g}$

$g=9.828m/s^2$

Attributions

This chapter contains material taken from

Openstax College Physics-Oscillatory Motion and Waves, and Openstax University Physics Volume 1 – Oscillations, and is used under a CC BY 4.0 license. Download these books for free at Openstax

To see what was changed, refer to the List of Changes

The section on Stability and Center of Mass is taken from

College Physics-Openstaxcollege

Questions and problems

Questions

What differentiates Simple Harmonic Motion from other periodic motions? Give examples of periodic motions that are not simple harmonic.
[openstax college phys. quest. 16.8] Pendulum clocks are made to run at the correct rate by adjusting the pendulum’s length. Suppose you move from one city to another where the acceleration due to gravity is slightly greater, taking your pendulum clock with you, will you have to lengthen or shorten the pendulum to keep the correct time, with other factors remaining constant? Explain your answer.
[openstax univ. phys. 1. quest. 15.13] A pendulum clock works by measuring the period of a pendulum. In the springtime, the clock runs with perfect time, but in the summer and winter, the length of the pendulum changes. When most materials are heated, they expand. Does the clock run too fast or too slow in the summer? What about the winter?
A block is attached to a horizontal spring undergoes SHM on a frictionless horizontal surface. How are the period and frequency affected if the mass is doubled?
How does doubling the amplitude of a mass-spring system affect the following parameters? In each case, explain your reasoning.
1. maximum speed.
2. frequency of oscillations
3. the total energy of the system
A block is attached to a horizontal spring and undergoes SHM. Explain how each of the following parameters would change and how if there was friction between the block and the surface. Explain your reasoning.
1. The frequency
2. The period
3. The amplitude
4. The speed when the block passes the equilibrium point
5. The amplitude
6. The total mechanical energy

Problems

[openstax univ. phys. 1. prob 15.30] A 0.500kg mass suspended from a spring oscillates with a period of 1.50s. How much mass must be added to the object to change the period to 2.00s?
[openstax univ. phys. 1. prob 15.57] A diver on a diving board is undergoing SHM. Her mass is 55.0kg and the period of her motion is 0.800s. The next diver’s period of simple harmonic oscillation is 1.05s. What is the second diver’s mass? The mass of the board is negligible.
A 5.00kg block is attached to a horizontal spring and placed on a horizontal frictionless surface. The spring constant is 100N/m. The block is pulled 4.00cm from its equilibrium position and let go. Once released, the block undergoes a SHM between x=-4.00cm and x=4.00cm.
1. Determine the position as a function of time.
2. What is the maximum speed of the block?
3. How long after being released does the block have its maximum speed for the first time?
4. What is the acceleration of the block at t=3.00s?
The acceleration due to gravity on the surface of the moon is 1.63m/s². If a pendulum with a period of 1.50s on Earth is taken to the moon, what would be its new period?
A 2.00kg package is suspended from a vertical spring. the spring stretches by 25.0cm when the package is at equilibrium. Once at equilibrium, the package is pulled down by 10.0cm and released.
1. Determine the spring constant.
2. Calculate the angular frequency of oscillations.
3. Write the equation for the position as a function of time.
A child on a playground swing moves back and forth like a pendulum. The length of the swing is 2.50m. Assume the swinging angle stays small.
1. Determine the maximum speed if the swing reaches an angle of 15.0°.
2. How long does it take for the child to swing back and forth five times?
3. How does your answer to (b) change if the maximum angle of swing is reduced to 7.5°? Explain your reasoning.
A 0.500kg glider on a frictionless air track is connected to a spring with a spring constant of 80.0N/m. A person does 0.400J of work to pull the glider away from its equilibrium position. Once released, the glider undergoes simple harmonic motion.
1. Determine the period of oscillations.
2. Determine the amplitude of oscillations.
3. Find the maximum speed of the glider
4. How long after being released does the glider have a speed of 0.500m/s?
5. What is the magnitude of its acceleration at that instant?
A block of mass 3.5kg is attached to a horizontal spring and undergoes SHM on a frictionless surface. Below is the graph of position vs time for this block.

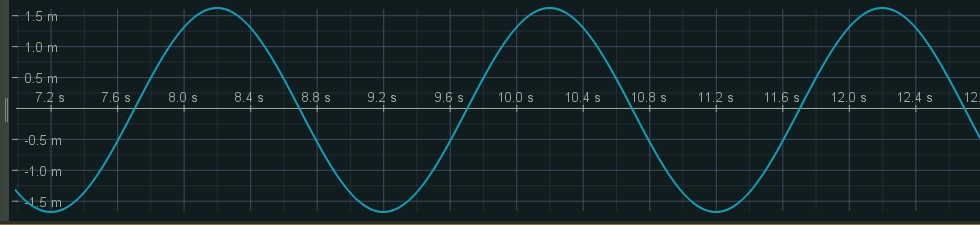
fig-prob13.8
1. Determine the spring constant.
2. The SHM starts by pulling the block away from the equilibrium and releasing it. Determine position as a function of time.
3. What is the total energy of the system?
A seismograph sensor uses a mass-spring system to detect ground motion. A 0.750kg mass is connected to a vertical spring with a spring constant of 200N/m. During a tremor, the system oscillates with an amplitude of 4.00cm.
1. Determine the angular frequency, ω, and period of oscillations.
2. Write the equation for the position as a function of time assuming the mass is released from maximum displacement.
3. What is the speed when the mass is 2.50cm away from the equilibrium point?
A diver stands at the end of a diving board that oscillates vertically after the diver jumps off. The board that has a mass of 5.00kg acts like a spring with a spring constant of 500N/m and continues to oscillate with an amplitude of 8.00cm.
1. Determine the period of oscillation.
2. What is the maximum restoring force acting on the board?
3. Calculate the total mechanical energy of the diving board while it is oscillating.
A tuning fork undergoes simple harmonic motion as it vibrates with a frequency of 440Hz and an amplitude of 0.300mm.
1. What is the maximum acceleration of the tip of the tuning fork?
2. Write the equation for position, and velocity as a function of time.
The position as a function of time for a mass-spring system undergoing a SHM is x=(0.500m)cos[(400rad/s)t].
1. Determine the amplitude, the frequency, and the period of oscillation.
2. What is the position at t=1.50s?
3. How much potential energy and kinetic energy does the system have at t=1.50s?
4. At what instant is the mass at x=0.200m for the first time?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License