Fluids
Unit 16 – Fluid Statics and Dynamics
Last Update: 06/09/2025
Common phases of matter consist of solid, liquid, gas, and plasma. Solids have a definite shape and a specific volume. The atoms in solids are in close contact. Forces between the atoms allow the atoms to vibrate, but not to change positions with neighboring atoms. A solid cannot be easily deformed because the atoms that make up the solid are not able to move about freely.
Liquids also have a definite volume, but in contrast with solids, liquids deform easily and take the shape of the container they are in. This is because in liquids the molecules are free to slide about and change neighbors – that is they flow, and therefore, they are a type of fluid.
Molecules in gases and charged particles in plasmas are separated by distances that are large compared with the size of the particles. The forces between the particles are therefore very weak, except when they collide with one another. Gases and plasma thus not only flow and are therefore considered to be fluids, but they are relatively easy to compress because there is much space and little force between the particles. Plasmas are difficult to contain because they have so much energy.
In this book, when discussing how substances flow, we will generally refer to both gases and liquids simply as fluids, and make a distinction between them only when they behave differently.
Density and pressure
density
Which weighs more, a ton of feathers or a ton of bricks? This old riddle plays with the distinction between mass and density. A ton is a ton, of course; but bricks have much greater density than feathers, and so we are tempted to think of them as heavier. In the riddle, the masses are the same, but the volume occupied by the feathers is much greater since their density is much lower. Density is defined as mass per unit volume and measured in kg/m3.
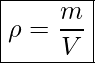
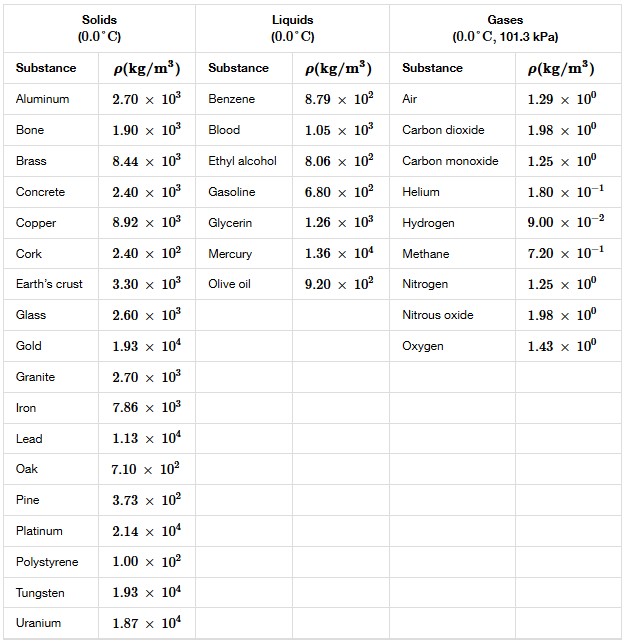
Notice that the densities of liquids and solids are roughly comparable, consistent with the fact that their atoms are in close contact. The densities of gases are much less than those of liquids and solids because the atoms in gases are separated by large amounts of empty space. The gases are displayed for a standard temperature of 0.0°C and a standard pressure of 101.3 kPa, and there is a strong dependence of the densities on temperature and pressure.
Pressure
Pressure is defined as force divided by the area perpendicular to the force, over which the force is applied. In the SI system, pressure is measured in units of Pascal, Pa=N/m.
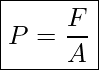
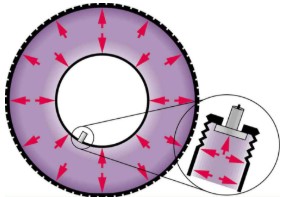
In a static fluid, the forces due to pressure are always exerted perpendicular to any surface. Furthermore, pressure is exerted on all surfaces. Swimmers, as well as the tire, feel pressure on all sides.
 |
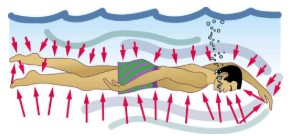 |
At the Earth’s surface, the air pressure exerted on you is a result of the weight of air above you. This pressure is reduced as you climb up in altitude and the weight of air above you decreases. Underwater, the pressure exerted on you increases with increasing depth. In this case, the pressure being exerted upon you is a result of both the weight of the water above you and that of the atmosphere above you. Let’s investigate the variation of pressure with depth in a fluid.
Consider the container shown below. Its bottom supports the weight of the fluid in it. Let us calculate the pressure exerted on the bottom by the weight of the fluid. That pressure is the weight of the fluid, mg, divided by the area, A, supporting it (the area of the bottom of the container): ![]()
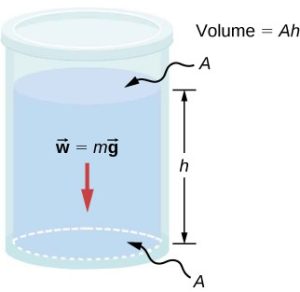
we can find the mass of the fluid from its volume and density. ![]()
The volume of the fluid, V, is related to the dimensions of the container. It is ![]() where A is the cross-sectional area and h is the depth. Combining the last two equations gives
where A is the cross-sectional area and h is the depth. Combining the last two equations gives ![]() .
.
If we enter this into the expression for pressure, we obtain ![]() .
.
So, the hydrostatic pressure due to the weight of the fluid is
![]()
The anti-intuitive result is that the hydrostatic pressure depends only on the height of the fluid, and not the amount of fluid above. So the pressure at the bottom of a 2m long straw filled with water is the same as the pressure 2m below the surface of the ocean.
For liquids, which are nearly incompressible, this equation holds to great depths. For gases, which are quite compressible, one can apply this equation as long as the density changes are small over the depth considered.
On the surface of the earth, the atmospheric pressure is due to the weight of the air above a given height. The atmospheric pressure at the earth’s surface varies a little due to the large-scale flow of the atmosphere induced by the earth’s rotation. The average atmospheric pressure at sea level is 1.01×105Pa. This value defines another common unit for pressure, known as atmosphere (atm).
![]()
Notice that ![]() is the pressure due to the weight of the fluid in the container. This pressure is relative to the atmospheric pressure and is called the gauge pressure. The total pressure is due to the weight of air and the weight of the fluid. This total pressure is called the absolute pressure.
is the pressure due to the weight of the fluid in the container. This pressure is relative to the atmospheric pressure and is called the gauge pressure. The total pressure is due to the weight of air and the weight of the fluid. This total pressure is called the absolute pressure.
![]()
Example 16.1
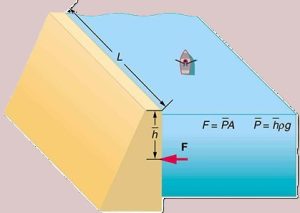
A water reservoir has a surface area of 500mX500m and a depth of 80.0m.
a) Find the mass of water that is held behind the dam.
b) What is the average pressure on the dam at a depth of 40.0m due to the water?
c) Calculate the force exerted against the dam at this depth and compare it with the weight of water behind the dam.
Solution
a) We can determine the mass of the water by using density and volume.
![]()
![]()
![]()
b) The average pressure due to the weight of water at a depth of 40.0m is
![]()
![]()
![]()
To put this in perspective, this gauge pressure is roughly 4 times the atmospheric pressure.
Note that the pressure found in part (b) is completely independent of the width and length of the lake—it depends only on its average depth at the dam. Consider the gigantic Hoover Dam shown below. There is a huge amount of water behind the dam as shown in fig16.6(b) and it is tempting to think that the amount of water is the reason such a strong structure is needed to hold it back. But even if all the water was removed and only a very thin layer with the same depth remained as shown in fig16.6(c), the hydrostatic pressure on the dam would still be the same!

 |
 |
c) The force on the dam can be calculated by using the definition of pressure,
![]()
![]()
![]()
The weight of water behind the dam is
![]()
![]()
![]()
To compare the two, let’s calculate their ratio.
![]()
![]()
So the force on the dam at a depth of 40.0m is about 8% of the weight of water behind the dam. Thus, the force on the dam depends only on the water’s average depth and the dimensions of the dam, not on the horizontal extent of the reservoir. In the diagram, the thickness of the dam increases with depth to balance the increasing force due to the increasing pressure.
Example 16.2
Calculate the average density of the atmosphere, given that it extends to an altitude of 120km. Compare this density with that of air listed in Table 16.1.
Solution
We can find the density at sea level.
![]()
![]()
![]()
![]()
This result is the average density of air between the Earth’s surface and the top of the Earth’s atmosphere, which essentially ends at 120 km. The density of air at sea level is given in Table 16.1 as 1.29kg/m3—about 15 times its average value. Because air is so compressible, its density has its highest value near the Earth’s surface and declines rapidly with altitude.
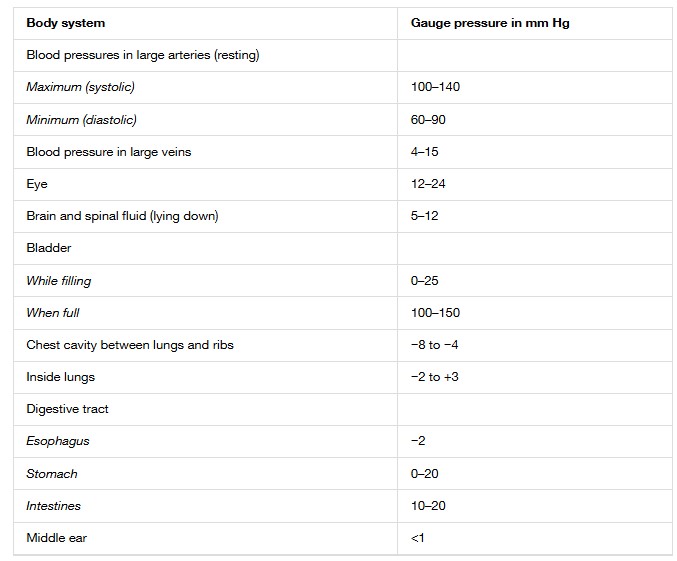
Typical Pressures in Human Body
Pascal’s Principle
Can pressure be increased in a fluid by pushing directly on the fluid? Yes, but it is much easier if the fluid is enclosed. The heart, for example, increases blood pressure by pushing directly on the blood in an enclosed system (valves closed in a chamber). If you try to push on a fluid in an open system, such as a river, the fluid flows away. An enclosed fluid cannot flow away, so the pressure is more easily increased by an applied force.
What happens to pressure in an enclosed fluid? Since atoms in a fluid are free to move about, they transmit the pressure to all parts of the fluid and the walls of the container. Remarkably, the pressure is transmitted undiminished. This phenomenon is called Pascal’s principle because it was first clearly stated by the French philosopher and scientist Blaise Pascal (1623–1662).
Pascal’s Principle states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and the walls of its container.
Pascal’s principle implies that the total pressure in a fluid is the sum of the pressures from different sources.
Application of Pascal’s principle
One of the most important technological applications of Pascal’s principle is found in a hydraulic system, which is an enclosed fluid system used to exert forces. Let us first consider the simple hydraulic system shown below.
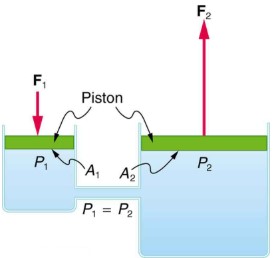
We can derive a relationship between the forces in the simple hydraulic system shown above by applying Pascal’s principle. Note first that the two pistons in the system are at the same height, so there will be no difference in pressure due to a difference in depth. Now, the pressure due to F1 acting on area A1 is simply ![]() . According to Pascal’s principle, this pressure is transmitted undiminished throughout the fluid and to all walls of the container. Thus,
. According to Pascal’s principle, this pressure is transmitted undiminished throughout the fluid and to all walls of the container. Thus, ![]() .
.
But since ![]() , we see that
, we see that ![]()
Hydraulic systems can increase or decrease the force applied to them. To make the force larger, the pressure is applied to a larger area. For example, if a 100-N force is applied to the left cylinder and the right one has an area five times greater, then the force out is 500 N.
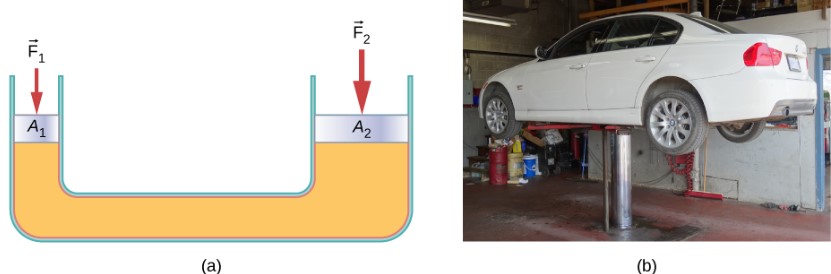
The hydraulic jack is such a hydraulic system. A hydraulic jack is used to lift heavy loads, such as the ones used by auto mechanics to raise an automobile. It consists of an incompressible fluid in a U-tube fitted with a movable piston on each side. One side of the U-tube is narrower than the other. A small force applied over a small area can balance a much larger force on the other side over a larger area.
The movement of the legs of a jumping spider is achieved partly by hydraulics. Using hydraulics, a jumping spider can create a force that makes it capable of jumping 25 times its length!
A simple hydraulic system can increase the force but not the energy. The conservation of energy applied to a hydraulic system tells us that the system cannot do more work than is done on it. Work transfers energy, and so the work output cannot exceed the work input.
Pascal demonstrated this principle with his famous exploding barrel demonstration. See this video for a reproduction of this experiment along with excellent commentary that clarifies the physics behind it. https://www.facebook.com/watch/?v=2215748075102771
Measurement of pressure
Manometers
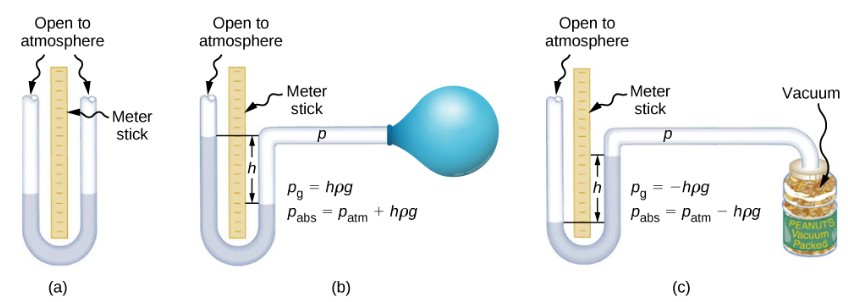
One of the most important classes of pressure gauges applies the property that pressure due to the weight of a fluid of constant density is given by ![]() . The U-shaped tube shown below is an example of a manometer; in part (a), both sides of the tube are open to the atmosphere, allowing atmospheric pressure to push down on each side equally so that its effects cancel.
. The U-shaped tube shown below is an example of a manometer; in part (a), both sides of the tube are open to the atmosphere, allowing atmospheric pressure to push down on each side equally so that its effects cancel.
A manometer with only one side open to the atmosphere is an ideal device for measuring gauge pressures. The gauge pressure is ![]() and is found by measuring h. For example, suppose one side of the U-tube is connected to some source of pressure such as the balloon in part (b) of the figure or the vacuum-packed peanut jar shown in part (c). Pressure is transmitted undiminished to the manometer, and the fluid levels are no longer equal. In part (b), the pressure transmitted by the balloon is greater than atmospheric pressure, whereas in part (c), the pressure transmitted by the vacuum-packed peanuts is less than atmospheric pressure. In both cases, the absolute pressure differs from atmospheric pressure by an amount
and is found by measuring h. For example, suppose one side of the U-tube is connected to some source of pressure such as the balloon in part (b) of the figure or the vacuum-packed peanut jar shown in part (c). Pressure is transmitted undiminished to the manometer, and the fluid levels are no longer equal. In part (b), the pressure transmitted by the balloon is greater than atmospheric pressure, whereas in part (c), the pressure transmitted by the vacuum-packed peanuts is less than atmospheric pressure. In both cases, the absolute pressure differs from atmospheric pressure by an amount ![]() where ρ is the density of the fluid in the manometer. In part (b), the absolute pressure can support a column of fluid of height h, so it must exert a pressure
where ρ is the density of the fluid in the manometer. In part (b), the absolute pressure can support a column of fluid of height h, so it must exert a pressure ![]() greater than atmospheric pressure (the gauge pressure is positive). In part (c), atmospheric pressure can support a column of fluid of height h, so the absolute pressure is less than atmospheric pressure by an amount
greater than atmospheric pressure (the gauge pressure is positive). In part (c), atmospheric pressure can support a column of fluid of height h, so the absolute pressure is less than atmospheric pressure by an amount ![]() (the gauge pressure is negative).
(the gauge pressure is negative).
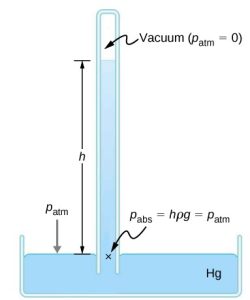
Barometers
Manometers typically use a U-shaped tube of a fluid (often mercury) to measure pressure. A barometer is a device that typically uses a single column of mercury to measure atmospheric pressure. The barometer, invented by the Italian mathematician and physicist Evangelista Torricelli (1608–1647) in 1643, is constructed from a glass tube closed at one end and filled with mercury. The tube is then inverted and placed in a pool of mercury. This device measures atmospheric pressure, rather than gauge pressure because there is a nearly pure vacuum above the mercury in the tube. The height of the mercury is such that ![]() . When atmospheric pressure varies, the mercury rises or falls.
. When atmospheric pressure varies, the mercury rises or falls.
Weather forecasters closely monitor changes in atmospheric pressure (often reported as barometric pressure), as rising mercury typically signals improving weather, and falling mercury indicates deteriorating weather. The barometer can also be used as an altimeter since average atmospheric pressure varies with altitude. Mercury barometers and manometers are so common that units of mm Hg are often quoted for atmospheric pressure and blood pressure.
Example 16.3
A U-tube with both ends open is filled with a liquid of density ρ1 to a height h on both sides. A liquid of density ρ2<ρ1 is poured into one side and Liquid 2 settles on top of Liquid 1. The heights on the two sides are different. The height to the top of Liquid 2 from the interface is h2 and the height to the top of Liquid 1 from the level of the interface is h1. Derive a formula for the height difference.
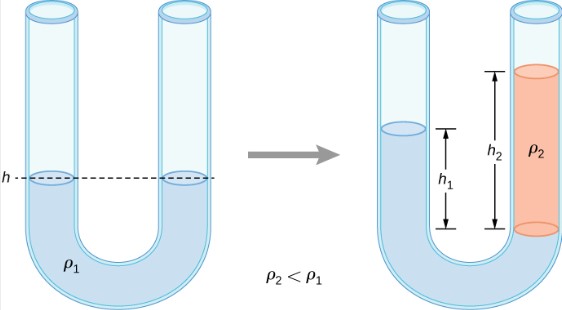
Solution
The pressure at points at the same height on the two sides of a U-tube must be the same as long as the two points are in the same liquid. Therefore, we consider two points at the same level in the two arms of the tube: One point is the interface on the side of the Liquid 2 and the other is a point in the arm with Liquid 1 that is at the same level as the interface in the other arm. The pressure at each point is due to atmospheric pressure plus the weight of the liquid above it.
![]()
![]()
Since P2=P1 ![]()
![]()
![]()
The result makes sense if we set ρ2=ρ1 which gives h_2=h_1. If the two sides have the same density, they have the same height.
Example 16.4
Intravenous infusions are usually made with the help of the gravitational force. Assuming that the density of the fluid being administered is 1.00 g/ml, at what height should the IV bag be placed above the entry point so that the fluid just enters the vein if the blood pressure in the vein is 18 mm Hg above atmospheric pressure? Assume that the IV bag is collapsible.
Solution
For the fluid to just enter the vein, its pressure at entry must exceed the blood pressure in the vein (18 mm Hg above atmospheric pressure). We therefore need to find the height of fluid that corresponds to this gauge pressure.
![]()
![]()
![]()
![]()
The IV bag must be placed at 0.24 m above the entry point into the arm for the fluid to just enter the arm. Generally, IV bags are placed higher than this. You may have noticed that the bags used for blood collection are placed below the donor to allow blood to flow easily from the arm to the bag, which is the opposite direction of flow than required in the example presented here.
Archimedes’ principle
Since pressure increases with depth in a fluid, the upward force on the bottom of an object in a fluid is greater than the downward force on top of the object. This net upward force is called the buoyant force. If the buoyant force is greater than the object’s weight, the net force on the object is upward. If we release such an object, it will rise in the fluid. If the buoyant force is less than the object’s weight, the object sinks when released. If the buoyant force equals the object’s weight, the object can remain suspended at its present depth, either immersed in the fluid (as for a neutrally buoyant diver) or partly above the surface (as with a floating object.)
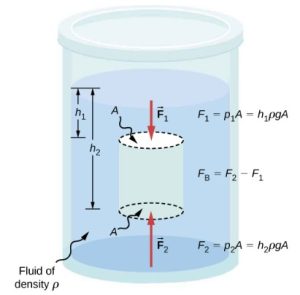
Archimede’s Principle: The buoyant force on an object is equal to the weight of the displaced fluid.
If you drop a lump of clay in water, it will sink. But if you mold the same lump of clay into the shape of a boat, it will float. Because of its shape, the clay boat displaces more water than the lump and experiences a greater buoyant force, even though its mass is the same. The same is true of steel ships.
The average density of an object is what ultimately determines whether it floats. If an object’s average density is less than that of the surrounding fluid, it will float. The reason is that the fluid, having a higher density, contains more mass and hence more weight in the same volume. The buoyant force, which equals the weight of the fluid displaced, is thus greater than the weight of the object. Likewise, an object denser than the fluid will sink.
Example 16.5
Suppose a person floats in freshwater with 97.0% of their volume submerged. What is the person’s average density?
Solution
Since the person floats, the buoyant force must equal their weight. The buoyant force is the weight of displaced water, which is the weight of a volume of water equal to 0.97 times the volume of the person.
![]()
![]()
![]()
![]()
![]()
Example 16.6
A large piece of solid steel with a mass of 1.00×107kg is completely submerged in water.
a) Calculate the buoyant force and compare it with the weight of the steel.
b) Calculate the buoyant force if this steel was shaped into a boat that could displace 1.00×105m3 of water. Would this boat sink or float?
Solution
a) To determine the buoyant force we need to determine the volume of the displaced fluid. Since this is the same as the volume of the solid steel, we need to use the density of steel to find this volume.
Density of steel: ρs=7.8×103kg/m3
![]()
![]()
![]()
This is also the volume of displaced water. Now we have to find the weight of the displaced water to get the buoyant force.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The weight of the steel is ![]()
![]()
![]() The weight of steel is significantly larger than the buoyant force. This boat will sink.
The weight of steel is significantly larger than the buoyant force. This boat will sink.
Fluid Dynamics
Fluid dynamics is the study of fluids in motion. Even the most basic forms of fluid motion can be quite complex. For this reason, we limit our investigation to ideal fluids in many of the examples. An ideal fluid is a fluid with negligible viscosity. Viscosity is a measure of the internal friction in a fluid. An ideal fluid is also incompressible —one for which an extremely large force is required to change the volume. In an incompressible fluid, the density is constant throughout. We will also limit our discussions to ideal fluids with laminar flow (or steady flow), as opposed to a turbulent flow.
equation of continuity – conservation of mass
Consider the flow of a fluid in the tube shown below. Since there is no loss of fluid, the amount of mass that passes point 1, Δm1, during the time interval Δm1 must equal the amount of mass that passes point 2 during the same time interval. Let’s represent the volume of mass Δm1 with ΔV1 and the density of the fluid with ρ.
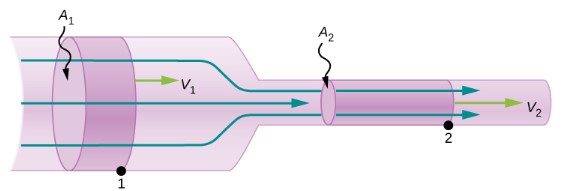
![]()
![]()
![]() where
where ![]() is the speed of the fluid at point 1.
is the speed of the fluid at point 1.
We can write a similar equation for the mass that passes point 2, Δm2, during the same time interval, Δt. Since Δm1=Δm2 we get
![]()
![]() Equation of Continuity
Equation of Continuity
The quantity ![]() is the same thing as
is the same thing as ![]() . We call this flow rate and represent it with Q. The equation of continuity is also known as the flow rate equation. Flow Rate is the volume of the fluid that passes a point per unit time.
. We call this flow rate and represent it with Q. The equation of continuity is also known as the flow rate equation. Flow Rate is the volume of the fluid that passes a point per unit time.
![]()
Example 16.7
A nozzle with a diameter of 0.500cm is attached to a garden hose with a radius of 0.900 cm. The flow rate through the hose and nozzle is 0.500 L/s.
a) Calculate the speed of the water in the hose.
b) Calculate the speed of the water in the nozzle.
Solution
a) First we need to convert L to m^3.
![]()
![]()
The cross-sectional area of the hose is
![]()
![]()
![]()
![]() the speed of water in the hose.
the speed of water in the hose.
b) Using the same strategy, we can determine the speed of water in the nozzle.
The cross-sectional area of the nozzle is
![]()
![]()
![]()
![]() the speed of water in the hose.
the speed of water in the hose.
Bernoulli’s equation – Conservation of energy
The application of the principle of conservation of energy to frictionless laminar flow leads to a very useful relation between pressure and flow speed in a fluid. This relation is called Bernoulli’s equation, named after Daniel Bernoulli (1700–1782).
Consider an incompressible fluid flowing through a pipe that has a varying diameter and height, as shown below. Subscripts 1 and 2 in the figure denote two locations along the pipe and illustrate the relationships between the areas of the cross sections A, the speed of flow v, the height from ground y, and the pressure p at each point. We assume here that the density at the two points is the same—therefore, density is denoted by ρ without any subscripts—and since the fluid is incompressible, the shaded volumes must be equal.
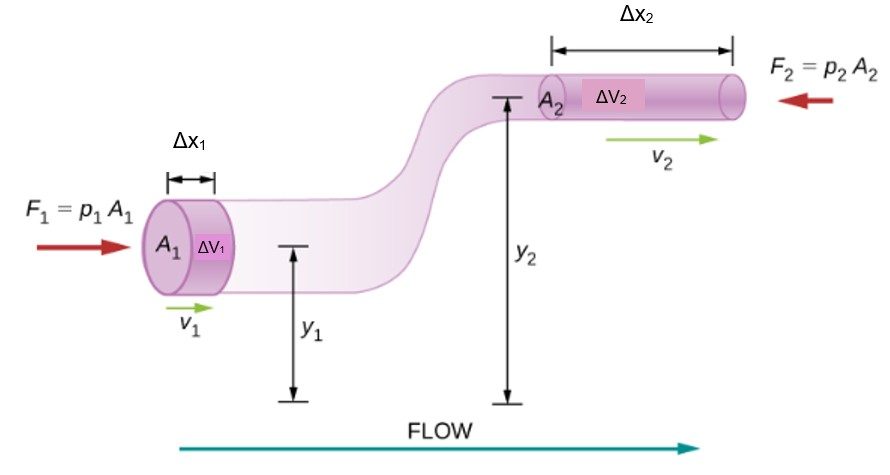
We also assume that there are no viscous forces in the fluid, so the energy of any part of the fluid will be conserved. To derive Bernoulli’s equation, we first calculate the work that was done on the fluid:
![]()
![]()
![]()
![]()
Now let’s calculate the change in the kinetic energy of the fluid.
![]()
![]()
![]()
The change in the gravitational potential energy is
![]()
![]()
![]()
Finally, using work-energy equation, ![]() , we get
, we get
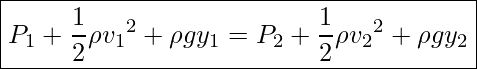 Bernoulli’s Equation
Bernoulli’s Equation
Notice that the terms in Bernoulli’s Equation can be interpreted as work or energy per unit volume.
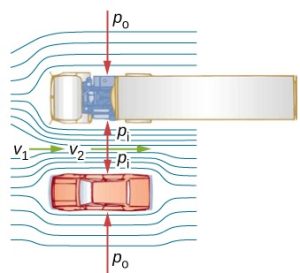
In a simpler situation where the elevation of the fluid does not change and y1=y2, Bernoulli’s equation provides a useful relationship between pressure and speed. An increase in the speed of the fluid results in a drop in pressure. This is also known as Bernoulli’s Principle. There are several common examples of pressure dropping in rapidly moving fluids. Shower curtains have a disagreeable habit of bulging into the shower stall when the shower is on. The high-velocity stream of water and air creates a region of lower pressure inside the shower and standard atmospheric pressure on the other side. The pressure difference results in a net force inward pushing the curtain in. You may also have noticed that when passing a truck on the highway, your car tends to veer toward it. The reason is the same—the high velocity of the air between the car and the truck creates a region of lower pressure, and the vehicles are pushed together by greater pressure on the outside.
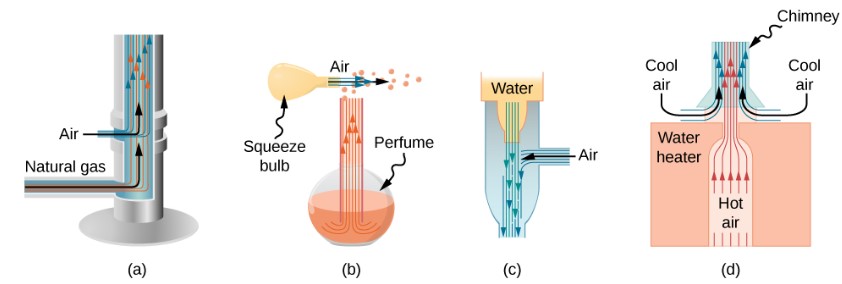
People have long put Bernoulli’s principle to work by using reduced pressure in high-velocity fluids to move things about. The following demonstrates some of the applications of Bernoulli’s principle.
Example 16.8
In Example 16.6, we found that the speed of water in a hose increased from 1.97 m/s to 25.5 m/s going from the hose to the nozzle. Calculate the pressure in the hose, if the hose is horizontal. Notice that since the nozzle is open to the air, the pressure at the nozzle is the same as atmospheric pressure, 1.01×105Pa.
Solution
Since the hose is horizontal and there is no change in elevation, Bernoulli’s Equation reduces to
![]()
![]()
![]()
Example 16.9
Fire hoses used in major fires have an inside diameter of 6.40cm. Suppose such a hose carries water with a flow rate of 40.0L/s to a height of 10.0m where it reaches a nozzle with an inside diameter of 3.00cm. What is the initial water pressure at the base of the hose?
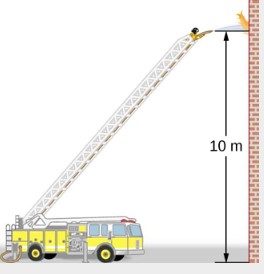
Solution
We first need to find the speed of water at the base and the nozzle, then we can use Bernoulli’s equation to determine the pressure at the base. Once again, since the nozzle is open to the air, the pressure at the nozzle is 1 atm=1.01×105Pa.
According to the Equation of Continuity, we know the flow rate stays constant. This can be used to find the speed.
![]()
![]()
![]() the speed at the base of the hose
the speed at the base of the hose
![]()
![]() the speed at the nozzle
the speed at the nozzle
Now, using Bernoulli’s Equation and setting y1=0, we get:
![]()
![]()
![]() This is the absolute pressure of water at the base of the hose.
This is the absolute pressure of water at the base of the hose.
Attributions
This chapter contains material taken from Openstax College Physics-Introduction to Fluid Statics and Dynamics, and Openstax University Physics Volume 1-Fluid Dynamics, and is used under a CC BY 4.0 license. Download these books for free at Openstax
questions and problems
questions
- [openstax-college phys-q11.3] Why are gases easier to compress than liquids or solids?
- [openstax-college phys-q11.16] Atmospheric pressure exerts a large force (equal to the weight of the atmosphere above your body—about 10 tons) on the top of your body when you are lying on the beach sunbathing. Why are you able to get up?
- [openstax-college phys-q11.19] The figure shows how sandbags placed around a leak outside a river levee can effectively stop the flow of water under the levee. Explain how the small amount of water inside the column formed by the sandbags can balance the much larger body of water behind the levee.
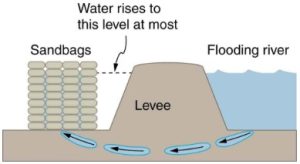
fig-quest16.3 - [openstax-college phys-q11.20] Why is it difficult to swim underwater in the Great Salt Lake?
- [openstax-college phys-q11.23] You can break a strong wine bottle by pounding a cork into it with your fist, but the cork must press directly against the liquid filling the bottle—there can be no air between the cork and the liquid. Explain why the bottle breaks, and why it will not if there is air between the cork and liquid.
- [openstax-college phys-q11.29] Do fluids exert buoyant forces in a “weightless” environment, such as in the space shuttle? Explain your answer.
- [openstax-college phys-q12.1] What is the difference between flow rate and fluid velocity? How are they related?
- [openstax-college phys-q12.12] Roofs are sometimes pushed off vertically during a tropical cyclone, and buildings sometimes explode outward when hit by a tornado. Use Bernoulli’s principle to explain these phenomena.
- [openstax-college phys-q12.14] It is dangerous to stand close to railroad tracks when a rapidly moving commuter train passes. Explain why atmospheric pressure would push you toward the moving train.
- Prove that pressure has the same units as energy (or work) per unit volume. In other words, 1 Pa= 1J/m3.
Problems
- [openstax-college phys-p11.2] Mercury is commonly supplied in flasks containing 34.5 kg (about 76 lb). What is the volume in liters of this much mercury?
- [openstax-college phys-p11.7] A trash compactor can reduce the volume of its contents to 0.350 their original value. Neglecting the mass of air expelled, by what factor is the density of the rubbish increased?
- [openstax-college phys-p11.8] A 2.50-kg steel gasoline can holds 20.0 L of gasoline when full. What is the average density of the full gas can, taking into account the volume occupied by steel as well as by gasoline?
- [openstax-college phys-p11.14] What depth of mercury creates a pressure of 1.00 atm?
- [openstax-college phys-p11.18] The aqueous humor in a person’s eye exerts a force of 0.300 N on the 1.10-cm2 area of the cornea. (a) What pressure is this in mm Hg? (b) Is this value within the normal range for pressures in the eye?
- [openstax-college phys-p11.20] What pressure is exerted on the bottom of a 0.500-m-wide by a 0.900-m-long gas tank that can hold 50.0 kg of gasoline when it is full?
- [openstax-college phys-p11.22] The left side of the heart creates a pressure of 120 mm Hg by exerting a force directly on the blood over an effective area of 15.0cm2. What force does it exert to accomplish this?
- [openstax-college phys-p11.26] A crass host pours the remnants of several bottles of wine into a jug after a party. He then inserts a cork with a 2.00-cm diameter into the bottle, placing it in direct contact with the wine. He is amazed when he pounds the cork into place and the bottom of the jug (with a 14.0-cm diameter) breaks away. Calculate the extra force exerted against the bottom if he pounded the cork with a 120-N force.
- [openstax-college phys-p11.30] Convert normal blood pressure readings of 120 over 80 mm Hg to newtons per meter squared using the relationship for pressure due to the weight of a fluid (P=hρg) rather than a conversion factor.
- [openstax-college phys-p11.33] Suppose you measure a standing person’s blood pressure by placing the cuff on his leg 0.500 m below the heart. Calculate the pressure you would observe (in units of mm Hg) if the pressure at the heart were 120 over 80 mm Hg. Assume that there is no loss of pressure due to resistance in the circulatory system (a reasonable assumption, since major arteries are large).
- [openstax-college phys-p11.36] What fraction of ice is submerged when it floats in freshwater, given the density of water at 0°C is very close to 1000 kg/m3 ?
- [openstax-college phys-p11.40] Bird bones have air pockets in them to reduce their weight—this also gives them an average density significantly less than that of the bones of other animals. Suppose an ornithologist weighs a bird bone in air and in water and finds its mass is 45.0 g and its apparent mass when submerged is 3.60 g (the bone is watertight).
- What mass of water is displaced?
- What is the volume of the bone?
- What is its average density?
- [openstax-college phys-p11.45] Consider a 2.00-L Helium balloon. Calculate the buoyant force on the balloon.
- [openstax-college phys-p11.68] During forced exhalation, such as when blowing up a balloon, the diaphragm and chest muscles create a pressure of 60.0-mm Hg between the lungs and chest wall. What force in newtons does this pressure create on the 600cm2 surface area of the diaphragm?
- [openstax-college phys-p12.1] What is the average flow rate in cm3/s of gasoline to the engine of a car traveling at 100 km/h if it averages 10.0 km/L?
- [openstax-college phys-p12.4] Blood is flowing through an artery with a radius of 2.0 mm at a rate of 40 cm/s. Determine the flow rate and the volume that passes through the artery in a period of 30 s.
- [openstax-college phys-p12.6] A major artery with a cross-sectional area of 1.00cm2 branches into 18 smaller arteries, each with an average cross-sectional area of 0.400cm2. By what factor is the average velocity of the blood reduced when it passes into these branches?
- [openstax-college phys-p12.11] Consider a fire hose with a 9.00-cm diameter carrying 80.0 L of water per second. What is the fluid speed?
- [openstax-college phys-p12.15] Water emerges straight down from a faucet with a 1.80-cm diameter at a speed of 0.500 m/s. Because of the construction of the faucet, there is no variation in speed across the stream.
- What is the flow rate in cm3/s?
- What is the diameter of the stream 0.200 m below the faucet?
- [openstax-college phys-p12.21] Every few years, winds in Boulder, Colorado, attain sustained speeds of 45.0 m/s (about 100 mi/h) when the jet stream descends during early spring. Approximately (ignoring turbulence) what is the force due to the Bernoulli effect on a roof having an area of 220m2? The typical air density in Boulder is 1.14kg/m3, and the corresponding atmospheric pressure is 8.89×104N/m2.
- [openstax-college phys-p12.23] Water flows at 40.0L/s from a 9.00-cm-diameter fire hose into a 3.00-cm-diameter nozzle.
- What is the pressure drop?
- Ignoring air resistance, to what maximum height above the nozzle can this water rise?
- [openstax-college phys-p12.27-modified] The left ventricle of a resting adult’s heart pumps blood at a flow rate of 83.0cm3/s, increasing its pressure by 110 mm Hg, its speed from zero to 30.0cm/s, and its height by 5.00 cm. (All numbers are averaged over the entire heartbeat.)
- Calculate the pressure (force per area) applied by the left ventricle. Hint: work done by the left ventricle changes the energy of the fluid (blood).
- Calculate the power output of the left ventricle. Hint: Use the units as a guide to figure out how to calculate power with the given information.
- [openstax-college phys-p12.28] A sump pump (used to drain water from the basement of houses built below the water table) is draining a flooded basement at the rate of 0.750 L/s, with an output pressure of 3.00×105N/m2. Neglect frictional losses
- The water enters a hose with a 3.00cm inside diameter and rises 2.50 m above the pump. What is its pressure at this point?
- The hose goes over the foundation wall, losing 0.500 m in height (so now it is 2.00m above the pump), and widens to 4.00cm in diameter. What is the pressure now?
- [openstax-univ. phys 1-p14.89-modifed]A container of water has a cross-sectional area of 0.100m2. A 20.0kg piston sits on top of the water. There is a spout located 0.150m from the bottom of the tank, open to the atmosphere, and a stream of water exits the spout. The cross-sectional area at the spout is 7.00×10-4m2.
- When the height of the water in the container is 0.500m, what is the speed of the water as it leaves the spout? Assume the water level goes down at a negligible speed.
- If the opening of the spout is located 2.50m above the ground, how far from the spout does the water hit the floor?
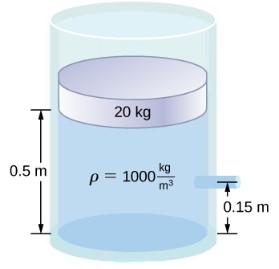
fig-prob16.24
