Thermodynamics
UNIT 19 – The First Law – Thermodynamic Processes
Last Update: 07/2/2024
the first law of thermodynamics
Thermodynamics is the branch of physics that deals with the transfer of heat energy and the relationship between heat energy and other forms of energy. Thermodynamics is useful in understanding the characteristics and behavior of macroscopic systems that contain a very large number of particles. An example of a thermodynamic system is a sample of gas in a container. In a thermodynamic system, the total of the kinetic and potential energies of all the particles in the system is called Internal Energy, U. Notice that the kinetic energy of the system itself or the location of the system as a whole and its potential energy does not affect the internal energy. For example, the internal energy of a gas in a container is not affected by moving the container from the floor to a table or by placing the container on a moving train.
The First Law of Thermodynamics is a statement of conservation of energy. We saw that work is a process in which energy is added or removed from a system. We also learned that heat transfer is a method of transferring energy to and from a system that occurs when there is a temperature difference. Work and heat transfer are the only mechanisms through which the internal energy of a system can change. The First Law of Thermodynamics states that the change in the internal energy of a system, ΔU, is equal to the difference between the energy that goes in and the energy that comes out. Since the transfer of energy takes place in the form of heat and/or work, The First Law of Thermodynamics is expressed as:
![]() 1st Law Of Thermodynamics – Conservation Of Energy
1st Law Of Thermodynamics – Conservation Of Energy
In this equation, Q is heat transferred into the system (energy going in), and W is work done by the system (energy coming out). By carefully using the correct signs for Q and W, this equation can be used for all situations regardless of whether heat is transferred into or out of the system, whether the system does work or work is done on the system by the surroundings.
We can rearrange this equation and write it as
![]() 1st Law of Thermodynamics- Conservation of Energy
1st Law of Thermodynamics- Conservation of Energy
In this text, we will use ![]() simply because it causes less confusion when it comes to determining the signs for Q and W. The sign conventions for Q and W are as follows.
simply because it causes less confusion when it comes to determining the signs for Q and W. The sign conventions for Q and W are as follows.
When heat flows into the system, Q >0.
When heat flows out of the system, Q<0.
When the system does work on its surroundings, W>0.
When the surroundings do work on the system, W<0.
Example 19.1
Suppose there is a heat transfer of 40.00 J to a system, while the system does 10.00 J of work. Later, there is a heat transfer of 25.00 J out of the system while 4.00 J of work is done on the system. What is the net change in the internal energy of the system?
Solution
We could approach this problem in two different ways. One way is to find the total heat transfer, and the total work, and then use the 1st law of thermodynamics (conservation of energy) to determine the change in the internal energy. The second way is to determine the change in the internal energy for each process and then add the two changes together.
First Method
|
|
|
![]()
![]()
![]()
Second Method
|
|
|
![]()
![]()
![]()
Thermodynamics deals with the relationship between heat transfer and other forms of energy. Let’s consider a sample of an ideal gas as our thermodynamic system. By definition, the internal energy is the sum of all the energies, potential plus kinetic, of all the molecules in the gas. Since forces among molecules are negligible in an ideal gas, there is no potential energy. Therefore the only type of molecular energy to consider in an ideal gas is kinetic energy. This means the internal energy of a sample of an ideal gas is the sum of the kinetic energy of all the molecules in the gas. Now, we are going to find an expression for the internal energy of a sample of a monatomic ideal gas and a sample of a diatomic ideal gas.
Internal Energy of a Sample of Monatomic Ideal Gas
We saw that absolute temperature is directly proportional to the average translational kinetic energy per molecule.
![]()
In a monatomic gas, the molecules can be treated as point particles and can only have translational kinetic energy. Therefore, we can easily find the internal energy of the system by simply multiplying the average translational kinetic energy per molecule by the number of molecules in the sample of gas.
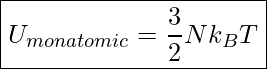 Internal Energy Of A Monatomic Gas
Internal Energy Of A Monatomic Gas
In this equation
![]() is the number of molecules in the sample of gas
is the number of molecules in the sample of gas
![]() is the Boltzmann Constant.
is the Boltzmann Constant. ![]()
![]() is the absolute temperature of the gas in Kelvin
is the absolute temperature of the gas in Kelvin
![]()
And since ![]() , we get
, we get
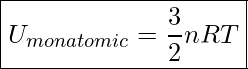 Internal Energy Of A Monatomic Gas
Internal Energy Of A Monatomic Gas
In this equation
![]() is the number of moles of gas
is the number of moles of gas
![]() is the Universal Gas Constant.
is the Universal Gas Constant. ![]()
![]() is the absolute temperature of the gas in Kelvin
is the absolute temperature of the gas in Kelvin
Internal Energy of a Sample of Diatomic Ideal Gas
Since a diatomic molecule can rotate as well as move along a straight line, Its total kinetic energy is the sum of its translational kinetic energy and rotational kinetic energy. Including rotational kinetic energy yields the following equation for the internal energy of a diatomic gas
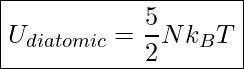 Internal Energy Of A Diatomic Gas
Internal Energy Of A Diatomic Gas
In this equation
![]() is the number of molecules in the sample of gas
is the number of molecules in the sample of gas
![]() is the Boltzmann Constant.
is the Boltzmann Constant. ![]()
![]() is the absolute temperature of the gas in Kelvin
is the absolute temperature of the gas in Kelvin
We can also express this equation in terms of the number of moles.
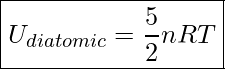 Internal Energy Of A Diatomic Gas
Internal Energy Of A Diatomic Gas
In this equation
![]() is the number of moles of gas
is the number of moles of gas
![]() is the Universal Gas Constant.
is the Universal Gas Constant. ![]()
![]() is the absolute temperature of the gas in Kelvin
is the absolute temperature of the gas in Kelvin
Notice that for an ideal gas, the internal energy is directly proportional to the absolute temperature of the gas.
Thermodynamic processes
A system is a section of the universe that is separated from its surroundings by real or hypothetical boundaries. A thermodynamic system is macroscopic and contains a large number of particles. For example, we can consider a gas confined to a cylinder to be a thermodynamic system. The quantities that describe the state of a thermodynamic system are known as state variables. In this book, we will only discuss thermodynamics as it pertains to ideal gases. For an ideal gas, state variables include (but are not limited to) pressure, volume, temperature, and the number of molecules or moles of the gas. The Ideal Gas Law, PV=nRT, is an equation that relates state variables for an ideal gas.
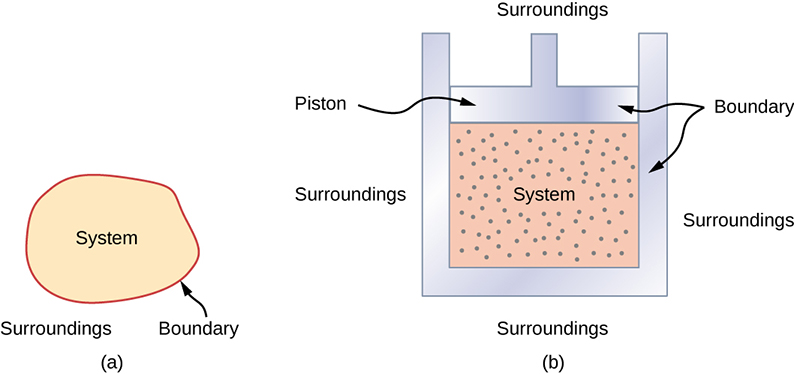
The state of a system can change as a result of its interaction with the environment. The interaction between a system and its environment involves the transfer of energy and this transfer of energy is governed by the First Law of Thermodynamics, Q=ΔU+W. Notice that internal energy, U, is the total energy of the particles in a system. At any given state the system has a certain amount of internal energy. Therefore, internal energy, U, is a state variable. On the other hand, heat transfer, Q, and work, W, represent energy flowing in and out of the system while the system is transitioning from one state to another state. Therefore Q and W are not state variables.
How the state of a system changes from an initial state to a final state is called a thermodynamic process. In this section, we discuss a few basic thermodynamic processes for an ideal gas.
isobaric process
An isobaric process is a process during which the pressure of the gas stays constant. For example, when a gas is confined to a cylinder with a piston that can move without friction, any heat that flows into the gas or out of the gas causes expansion or compression that occurs at constant pressure and is, therefore, isobaric. Let’s find an expression for work done in such an isobaric process.
Consider a sample of an ideal gas confined to a cylinder with a frictionless, moveable piston on top, as shown in Figure 19.1.
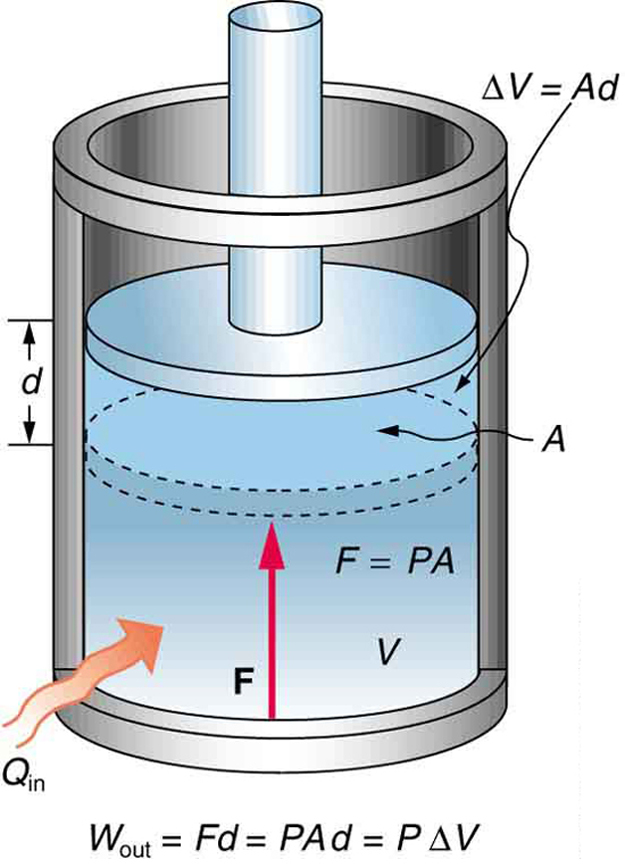
If heat is transferred into the system, the gas expands and pushes the piston upward. The work done in this process is the work done by force F applied by the gas to the piston to move it a distance d, as shown in Figure 19.1.
![]()
Since ![]() , and
, and ![]() . Since pressure is defined as force per unit area,
. Since pressure is defined as force per unit area, ![]() , we can replace
, we can replace ![]() with
with ![]() , and get
, and get
![]()
Furthermore, ![]() , where
, where![]() is the change in the volume of the gas (see Figure 18.1). Therefore,
is the change in the volume of the gas (see Figure 18.1). Therefore,
![]() Work Done In An Isobaric Process
Work Done In An Isobaric Process
Notice that if the gas expands, ![]() and
and ![]() . If, on the other hand, someone pushes down on the piston to compress the gas, then
. If, on the other hand, someone pushes down on the piston to compress the gas, then ![]() and
and ![]() .
.
We often show a thermodynamic process with a plot of pressure vs volume, called a PV diagram. Each point on a PV diagram corresponds to a specific pressure, volume, and temperature and represents a specific state of the gas. The PV diagram for an isobaric expansion from state A to state B is shown in Figure 19.2
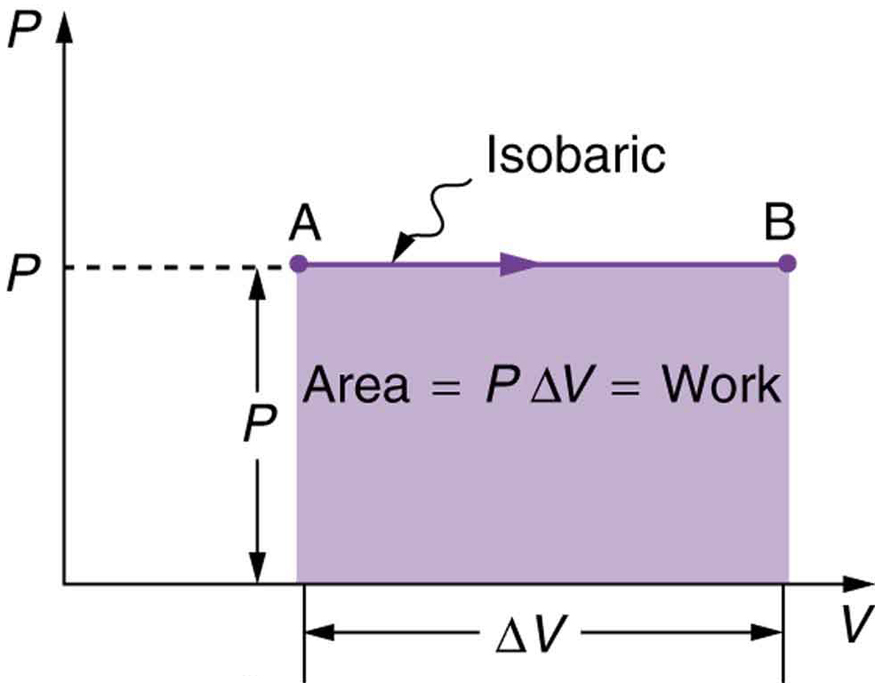
It’s easy to see that the area under this line is equal to the work done in this process. This idea can be generalized to any process. The area under the plot of pressure vs volume is always equal to the work done in that process.
isochoric (isometric) process
An isochoric (isometric) process is a process during which the volume of the gas stays constant. Since an isochoric process on a PV diagram is a straight vertical line, the work done in an isochoric process is zero. Applying the First Law of Thermodynamics we get
![]() For An Isochoric Process
For An Isochoric Process
To create an isochoric process, the gas must be confined to a rigid container with a fixed volume.
Example 19.2
Consider the expansions of an ideal gas between the equilibrium states A and C as shown in the PV diagram below. If 515 J of heat is added to the gas as it follows the path ABC, how much heat is required for the transition along ADC?
Assume that P1=2.10×105Pa, P2=1.05×105Pa, V1=2.25×10-3m3 , V2=4.50×10-3m3.
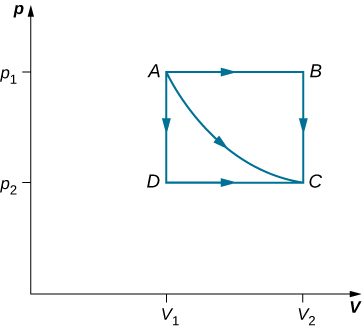
Solution
In both expansions, the initial state is A and the final state is C. Since the change in internal energy, ΔU, depends only on the temperature change, ΔU is the same in both expansions.
Let’s apply the first law of thermodynamics to these two processes.
For the expansion along the path ABC. Since AB is an isobaric process, WAB=P1ΔVAB
![]()
![]()
![]()
![]()
Now, let’s do the same thing for the expansion along ADC.
![]()
![]()
![]()
![]()
Discussion
The work calculations in this problem are made simple since no work is done along AD and BC (isometric processes). Along AB and DC; the pressure is constant over the volume change(isobaric processes), so the work done is simply PΔV.
Isothermal process
An isothermal process is a process during which the temperature of the gas stays constant. We can use the ideal gas law to predict the shape of an isothermal process on a PV diagram.
![]()
![]()
In an isothermal process ![]() . This means P is inversely proportional to V. The graph of an inverse function (
. This means P is inversely proportional to V. The graph of an inverse function (![]() ) is a hyperbola as shown in Figure 18.4-a.
) is a hyperbola as shown in Figure 18.4-a.
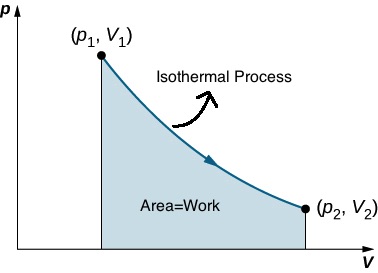
Using calculus, it can be shown that the area under an isothermal curve from state 1 to state 2 is equal to
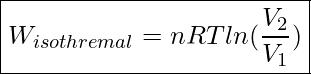 Work In An Isothermal Process
Work In An Isothermal Process
As mentioned earlier, the internal energy of an ideal gas is directly proportional to its absolute temperature. Therefore, in an isothermal process, there is no change in the internal energy, and ![]() . Applying the First Law of Thermodynamics we get
. Applying the First Law of Thermodynamics we get
![]() For An Isothermal Process
For An Isothermal Process
One way to keep the temperature of a gas constant as the gas expands or contracts is by making the process occur very slowly in a container with walls that are an excellent conductor of heat and placed in a reservoir at a constant temperature. For example, consider the following setup where a cylinder of gas with a movable piston is immersed in a large water tank whose temperature is maintained constant. Since the piston is freely movable, the pressure inside Pin is balanced by the pressure outside Pout by some weights on the piston.

Slowly removing the weights results in an isothermal expansion of the gas. This is because removing the weights on the piston leads to an imbalance of forces on the piston, which causes the piston to move up. As the piston moves up, the temperature is lowered momentarily, which causes heat to flow from the heat bath to the system. This flow of heat causes the temperature to go back up till thermal equilibrium is, once again, restored. So, effectively, the temperature of the gas stays constant as the gas slowly expands.
Note that all phase changes are also isothermal processes.
As mentioned earlier, isothermal processes create hyperbolic curves on a PV diagram. The higher the temperature, the higher up is the position of the curve on the PV diagram, as shown below.
Adiabatic process
An adiabatic process is a process in which there is no transfer of heat between the system and the environment. Since ![]() then
then
![]() For An Adiabatic Process
For An Adiabatic Process
Notice that a change in internal energy, U, is always accompanied by a change in temperature. When an ideal gas is compressed adiabatically<span id=”MathJax-Element-1925-Frame” class=”MathJax” style=”font-style: normal;font-weight: normal;line-height: normal;font-size: 14px;text-indent: 0px;text-align: left;text-transform: none;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;padding: 0px;margin: 0px” role=”presentation” data-mathml=”
(Q=0),(Q=0),
“>, work is done on it, and its temperature increases; in an adiabatic expansion, the gas does work, and its temperature drops. Therefore, if in a process, there is no transfer of heat to or from the system, then the temperature of the system must change.
One way to produce an adiabatic process is to make the process happen very quickly and leave no time for heat transfer. Adiabatic compressions occur in the cylinders of a car, where the compressions of the gas-air mixture take place so quickly that there is no time for the mixture to exchange heat with its environment. Nevertheless, because work is done on the mixture during the compression, its temperature does rise significantly. In fact, the temperature increases can be so large that the mixture can explode without the addition of a spark. Such explosions, since they are not timed, make a car run poorly—it usually “knocks.” Because ignition temperature rises with the octane of gasoline, one way to overcome this problem is to use higher-octane gasoline.
Another way to produce an adiabatic process is to use perfect insulation around a system to prevent heat transfer. For example, in Figure 19.5, even if the grains of sand are removed one at a time from the top of the piston to allow the gas to expand very slowly, insulation around the cylinder prevents heat transfer, and the temperature of the gas drops as it expands.
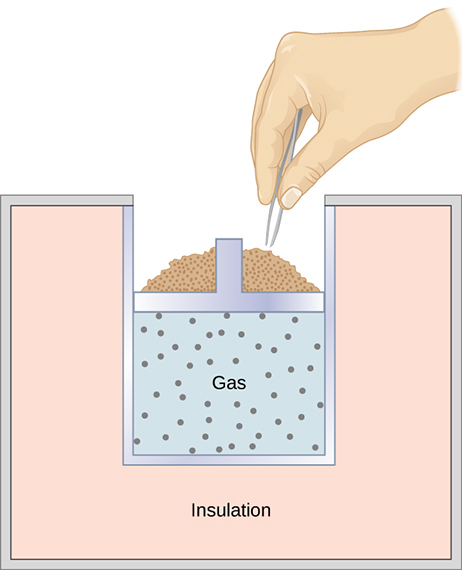
The PV diagram for an adiabatic process is a curve. Starting from the same pressure and volume, an adiabatic expansion produces a curve that is below the isothermal expansion starting from the same state. This is shown in Figure 19.6

In an adiabatic process from state 1 to state 2, pressure and volume are related according to
![]() For An Adiabatic Process
For An Adiabatic Process
where ![]() .
.
![]() is the specific heat at constant pressure, and
is the specific heat at constant pressure, and ![]() is the specific heat at constant volume. In the next section, we explore the difference between the two values of specific heat for an ideal gas.
is the specific heat at constant volume. In the next section, we explore the difference between the two values of specific heat for an ideal gas.
Example 19.3
An ideal gas expands isothermally along AB and does 700 J of work (see below).
(a) How much heat does the gas exchange along AB?
(b) The gas then expands adiabatically along BC and does 400 J of work. When the gas returns to A along CA, it exhausts 100 J of heat to its surroundings. How much work is done on the gas along this path?
Solution for (a)
Let’s apply the first law of thermodynamics to the process AB. But since the process is isothermal, there is no change in the internal energy of the gas, and we get
![]()
![]()
Solution for (b)
Since process BC is adiabatic, Q=0. Therefore,, using the first law of thermodynamics, and using the fact that the gas does 400J of work, we get
![]()
![]()
Now let’s apply the first law for the process CA, and use the fact that 100J of heat is released.
![]()
![]()
For the whole cyclic process of going from A to B to C and back to A, the change in internal energy must be zero because the gas started and ended at the same state and therefore at the same temperature. This means that
![]()
![]()
![]()
Specific Heat at Constant Pressure (CP) vs Specific Heat at Constant Volume (CV)
We defined the specific heat of solids and liquids as the amount of heat needed to change the temperature of 1kg of a substance by 1°C. Since the behavior of gases and ideal gas law depend on the number of moles of the gas and not its mass, for gases, we use molar specific-heat capacity. Molar specific heat capacity is defined as the amount of heat needed to change the temperature of 1mol of gas by 1°C.
Consider two identical samples of an ideal gas, with the same pressure, temperature, volume, and the number of moles. One sample is confined to a rigid container with a fixed volume (Vessel A in Figure 19.7), and the other one is in a cylinder equipped with a freely moving piston (Vessel B in Figure 19.7)
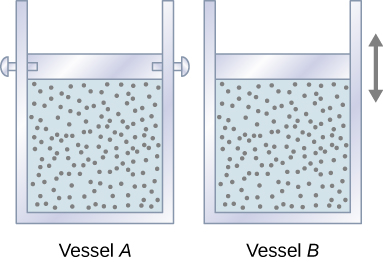
Which sample needs to receive more heat for its temperature to go up by 1°C? Since the gas in vessel A cannot expand and do work, all the energy added to the system in the form of heat is going to increase the average kinetic energy of the molecules, and, as a result, increase the temperature. In vessel B, however, some of the energy added in the form of heat is leaving the system in the form of work as the gas expands. This means that only some of the heat energy is contributing to the increase in the average kinetic energy of the molecules and causing the temperature to go up. More heat needs to be added to vessel B to cause the same 1°C temperature change as in vessel A. Therefore, heat capacity at constant pressure is greater than heat capacity at constant volume.
![]()
Using the Ideal Gas Law it is possible to derive the values given for CP and CV in Table 19.1.
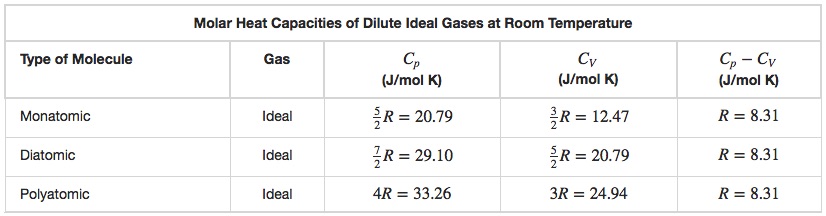
Using the values in Table 19.1, we see that
![]() and
and ![]() For Ideal Gases
For Ideal Gases
Example 19.4
2.00 mol of He gas that is initially at a temperature of 20.0ºC expands to three times its initial volume.
a) Calculate the work done, if the process was isothermal.
b) Calculate the work done, if the process was adiabatic.
Solution for (a)
Work done in an isothermal process is
![]()
![]()
![]()
Solution for (b)
In an adiabatic process, there is no transfer of heat and Q=0. Using the first law of thermodynamics we get:
![]()
![]()
Since He is a monatomic gas, the change in its internal energy is given by
![]()
So we need to find the final temperature. If we write the ideal gas law for the initial and final state and take into account that the number of moles, n, doesn’t change, we get
![]() and
and ![]() ⇒
⇒ ![]()
Since V2 = 3V1 we get
![]() OR
OR ![]()
For an adiabatic process, inital and final pressures and volumes are related according to
![]()
This results in
![]()
For a monatomic gas, γ=1.67.
![]()
![]()
Therefore T2 is
![]()
![]()
![]()
Now we can calculate the change in the internal energy of the gas during the expansion.
![]()
![]()
![]()
Since the process is adiabatic and Q=0,
![]()
![]()
Discussion
As demonstrated in Figure 18.6 (reproduced below), the curve for an adiabatic expansion is below the curve for an isothermal expansion on a PV diagram. Since work is the area under the plot of Pressure vs Volume, we expect the work done in the adiabatic expansion to be less than the work done in the isothermal expansion. This agrees with the numerical results in this problem.

Attribution
This chapter contains material taken from Openstax College Physics-Thermodynamics, and Openstax University Physics Volume 2-The First Law of Thermodynamics, and is used under a CC BY 4.0 license, . Download these books for free at Openstax
To see what was changed, refer to the List of Changes.
questions and Problems
Questions
- In what way are work and heat similar? In what way are they different?
- What is internal energy?
- Is it possible for a sample of an ideal gas to have more internal energy than another sample of the same gas but be at a lower temperature? Explain.
- Explain the difference between temperature, heat, and internal energy.
- Is it possible for a substance to absorb or release heat without any change in its temperature? Explain.
- Is it possible for a substance’s temperature to change while its internal energy stays constant? Explain.
- A sample of gas is compressed but its temperature stays constant throughout the process. How is that possible?
- Explain why a thermally insulated sample of gas can’t go through a thermodynamic process without experiencing a change in its temperature.
- What type of setup or procedure allows a gas to go through a thermodynamic process that is
- isobaric?
- adiabatic?
- isometric?
- isothermal?
- A certain amount of heat, Q, can be added to a sample of an ideal gas in three different ways: at a constant temperature, at a constant pressure, or a constant volume.
- Which process will result in the greatest amount of work?
- Which process will result in the greatest final temperature?
- Which process will result in the greatest final volume?
- Which process will result in the greatest final pressure?
problems
- [openstax univ. phys. vol.2 – 3.23]It takes 500 J of work to compress 0.500 mol of an ideal gas to one-fifth its original volume while the temperature of the gas stays constant. Determine that temperature.
- [openstax univ. phys. vol. 2 – 3.25] An ideal gas with a volume of 20.0L and pressure of 0.800atm expands isobarically. In this process, 500 J of work is done by the gas. Determine the final volume of the gas.
- In a thermodynamic process, 0.750mol of an ideal gas expands from 0.500L to 4.00 L at a constant temperature of 300K.
- What is the change in the internal energy of the gas?
- How much heat is absorbed by the gas in this process?
- [openstax univ. phys. vol. 2 – 3.48] An ideal monatomic gas at a pressure of 2.00×105Pa and a temperature of 300K undergoes an isobaric expansion from 2.00×103cm3 to 4.00×103cm3.
- What is the work done by the gas?
- What is the temperature of the gas after the expansion?
- How many moles of gas are there?
- What is the change in the internal energy of the gas?
- How much heat is added to the gas?
- [openstax univ. phys. vol.2 – 3.54-modified] Two (2.00) moles of a diatomic ideal gas at 5.00×106Pa and 5.00 L is expanded isothermally until the volume is doubled (step 1). Then it is cooled isochorically until the pressure is 1.00×106Pa (step 2). The temperature drops in this process. The gas is now compressed isothermally until its volume is back to 5.00 L, but its pressure is now 2.00×106Pa (step 3). Finally, the gas is heated isochorically to return to the initial state (step 4).
- Draw the four processes in the PV plane.
- Find the total work done from beginning to end. Is this work done on the gas or by the gas?
- Find the heat exchanged between the gas and the environment in each process. For each process, indicate whether heat is absorbed or released by the gas.
- Determine the total heat exchanged between the gas and the environment in this cycle.
- Determine the total change in the internal energy of the gas in this cycle.
- [openstax univ. phys. vol. 2 – 3.67(edited)] A monatomic ideal gas undergoes an adiabatic expansion in which its volume is doubled. How is the pressure of the gas changed?
- [openstax univ. phys. vol. 2 – 3.78] Two (2.00) moles of a monatomic ideal gas such as helium are compressed adiabatically from a state (3.00 atm, 5.00 L) to a state with a pressure of 4.00 atm.
- Find the volume of the final state.
- Find the temperature of the initial and final states of the gas.
- Find the work done by the gas in the process.
- Find the change in the internal energy of the gas in the process.
- [openstax univ. phys. vol. 2 – 3.87] Four (4.00) moles of a monatomic ideal gas in a cylinder at 27.0ºC expands at a constant pressure of 1.00 atm until its volume doubles.
- What is the change in internal energy?
- How much work was done by the gas in the process?
- How much heat was transferred to the gas?
- Consider the PV diagram of a series of thermodynamic processes shown below.
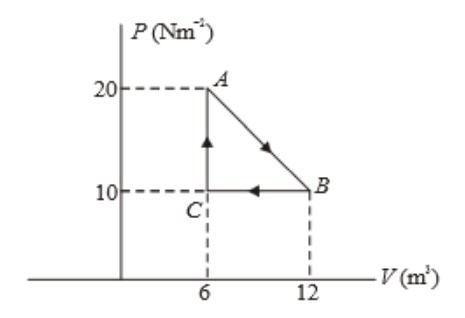
- Find the work done from A to B. Is this work done on the gas or by the gas?
- Find the work done from B to C. Is this work done on the gas or by the gas?
- Find the work done in the cycle.
- An ideal gas with pressure P1 and volume V1 expands to a state with volume V2 once isothermally, and a second time adiabatically.
- Draw these processes on a PV diagram.
- In which case there is more work done by the gas? Explain.
- An ideal gas with pressure P1 and volume V1 is compressed to a state with volume V2 once isothermally, and a second time adiabatically.
- Draw these processes on a PV diagram.
- In which case there is more work done on the gas? Explain.
- [openstax univ. phys. vol. 2 – 3.30] An ideal gas expands to three times its original volume. Which process requires more work from the gas, an isothermal process or an isobaric one? Determine the ratio of the work done in these processes.
- [openstax univ. phys. vol. 2 – 3.34] Calculate the internal energy of 15mg of helium at a temperature of 0°C.
- [openstax univ. phys. vol. 2 – 3.41] As Shown below, if the heat absorbed by the gas along AB is 400J, determine the quantities of heat absorbed along
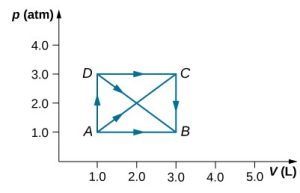
- ADB
- ACB
- ADCB
- [openstax univ. phys. vol. 2 – 3.76] An ideal gas expands from a volume of 2.0×10-3 m3 to 2.5×10-3 m3. The initial pressure and temperature were 5.0×105 Pa and 300K respectively. Find the final pressure and temperature if
- the process was adiabatic. Use γ=5/3 for the gas.
- the process was isothermal.
- [openstax univ. phys. vol. 2 – 3.95] One mole (1.0 mol) of an ideal gas is initially in a chamber of volume 1.0×10-2m3 and at a temperature of 27°C.
- How much heat is absorbed by the gas when it slowly expands isothermally to twice its initial volume?
- Suppose the gas is slowly taken to the same final state by first decreasing the pressure at constant volume and then expanding it isobarically. What is the heat transferred for this case?
- Calculate the heat transferred when the gas is taken to the same final state by expanding it isobarically, then decreasing its pressure at constant volume.


