Thermodynamics
UNIT 20 – The Second Law – Heat Engines and Thermal Pumps
Last Update: 07/04/2024
The second law of thermodynamics
The second law of thermodynamics deals with the direction taken by spontaneous processes. Many processes occur spontaneously in one direction only—that is, they are irreversible, under a given set of conditions. For example, as noted in the previous units, heat involves the transfer of energy from higher to lower temperatures. A cold object in contact with a hot one never spontaneously gets colder, transferring heat to the hot object and making it hotter. Furthermore, mechanical energy, such as kinetic energy, can be completely converted to thermal energy by friction, but the reverse is impossible. A hot stationary object never spontaneously cools off and starts moving. Yet another example is the expansion of a puff of gas introduced into one corner of a vacuum chamber. The gas expands to fill the chamber, but it never regroups in the corner. The random motion of the gas molecules could take them all back to the corner, but this is never observed to happen.
The fact that certain processes never occur suggests that there is a law forbidding them to occur. The first law of thermodynamics would allow them to occur—none of those processes violate the conservation of energy. The law that forbids these processes is called the second law of thermodynamics. We shall see that the second law can be stated in many ways that may seem different, but which in fact are equivalent. Like all natural laws, the second law of thermodynamics gives insights into nature, and its several statements imply that it is broadly applicable, fundamentally affecting many apparently disparate processes.
The already familiar spontaneous direction of heat transfer from hot to cold is the basis of our first version of the second law of thermodynamics.
The Second Law of Thermodynamics (First Version)
Heat transfer occurs spontaneously from higher- to lower-temperature bodies but never spontaneously in the reverse direction.
There is yet another way of expressing the second law of thermodynamics. This version relates to a concept called entropy. By examining it, we shall see that the directions associated with the second law—heat transfer from hot to cold—are related to the tendency in nature for systems to become disordered and for less energy to be available for use as work. The entropy of a system can in fact be shown to be a measure of the unavailability of energy to do work. Entropy is a measure of how much energy is not available to do work.
Entropy is represented with S and measured in units of Joules/Kelvin. Entropy is a state variable. This means the change in entropy from state 1 to state 2 is the same no matter what path the system takes to go from state 1 to state 2. In processes where heat transfer takes place at a constant temperature, we can calculate the change in entropy without using calculus.
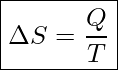 Change In Entropy At Constant Temperature
Change In Entropy At Constant Temperature
Spontaneous heat transfer from hot to cold is an irreversible process. Calculate the total change in entropy if 4000 J of heat transfer occurs from a hot reservoir at TH=327°C to a cold reservoir at TC=-23°C. By definition, a reservoir is so large that the heat transferred to or from it does not result in any significant change in temperature. Therefore, we can assume there is no temperature change in either reservoir.
Solution
To find the total change in entropy, we calculate the change in entropy of each reservoir separately and then add them together.
First convert both temperatures to Kelvin.
|
|
|
|
|
|
![]()
![]()
Entropy is a measure of disorder in a system. For example, melting a block of ice means taking a highly structured and orderly system of water molecules and converting it into a disorderly liquid in which molecules have no fixed positions, as shown in Figure 20.1

Example 20.2 – Change in Entropy of Ice Melting
Find the increase in entropy of 1.00 kg of ice originally at 0°C that is melted to form water at 0°C.
Solution
Heat absorbed by ice during this process is
![]()
![]()
![]()
This heat transfer occurs while the temperature is at 0°C=273K. Therefore, the change in entropy is
![]()
![]()
![]()
Discussion
This is a significant increase in entropy accompanying an increase in disorder.
In another easily imagined example, suppose we mix equal masses of water originally at two different temperatures, say 20.0°C and 40.0°C. The result is water at an intermediate temperature of 30.0°C. Three outcomes have resulted: entropy has increased, some energy has become unavailable to do work, and the system has become less orderly. Let us think about each of these results.
Mixing the two bodies of water has the same effect as heat transfer from the hot one and the same heat transfer into the cold one. The mixing decreases the entropy of the hot water but increases the entropy of the cold water by a greater amount, producing an overall increase in entropy (see Example 20.1). Second, once the two masses of water are mixed, there is only one temperature—you cannot run a heat engine with them (as we will see in the next section). The energy that could have been used to run a heat engine is now unavailable to do work. Third, the mixture is less orderly, or to use another term, less structured. Rather than having two masses at different temperatures and with different distributions of molecular speeds, we now have a single mass with a uniform temperature.
These three results—entropy, unavailability of energy, and disorder—are not only related but are in fact essentially equivalent.
Aatish Bhatia does a great job explaining the meaning of entropy and the Second Law of Thermodynamics using sheep.
The Second Law of Thermodynamics (Second Version)
The total entropy of an isolated system either increases or remains constant in any process; it never decreases.
The Second Law of Thermodynamics and Living Organisms
A living cell’s primary tasks of obtaining, transforming, and using energy to do work may seem simple. However, the second law of thermodynamics explains why these tasks are harder than they appear. None of the energy transfers and transformations in the universe is completely efficient. In every energy transfer, some amount of energy is lost in an unusable form. In most cases, this form is thermal energy. For example, when an airplane flies through the air, it loses some of its energy as heat energy due to friction with the surrounding air. This friction actually heats the air by temporarily increasing air molecule speed. Likewise, some energy is lost as heat energy during cellular metabolic reactions. This is good for warm-blooded creatures like us because heat energy helps to maintain our body temperature. Strictly speaking, no energy transfer is completely efficient, because some energy is lost in an unusable form.
An important concept in physical systems is that of order and disorder (or randomness). The more energy that a system loses to its surroundings, the less ordered and more random the system. Scientists refer to the measure of randomness or disorder within a system as entropy. High entropy means high disorder and low energy. To better understand entropy, think of a student’s bedroom. If no energy or work were put into it, the room would quickly become messy. It would exist in a very disordered state, one of high entropy. Energy must be put into the system, in the form of the student doing work and putting everything away, to bring the room back to a state of cleanliness and order.
Living things are highly ordered, requiring constant energy input to maintain themselves in a state of low entropy. As living systems take in energy-storing molecules and transform them through chemical reactions, they lose some amount of usable energy in the process, because no reaction is completely efficient. They also produce waste and by-products that are not useful energy sources. This process increases the entropy of the system’s surroundings. Since all energy transfers result in losing some usable energy, the second law of thermodynamics states that every energy transfer or transformation increases the universe’s entropy. Even though living things are highly ordered and maintain a state of low entropy, the universe’s entropy in total is constantly increasing due to losing usable energy with each energy transfer that occurs. Essentially, living things are in a continuous uphill battle against this constant increase in universal entropy.
heat engines
A heat engine is a device that uses heat transfer to do work. Figure 20.2 is a schematic diagram of a heat engine. Gasoline and diesel engines, jet engines, and steam turbines are all heat engines that do work by using part of the heat transfer from some source. In Figure 20.2 heat transfer from the hot object (or hot reservoir) is denoted as QH, while heat transfer into the cold object (or cold reservoir) is QC, and the work done by the engine is W. The temperatures of the hot and cold reservoirs areTH, and TC respectively.
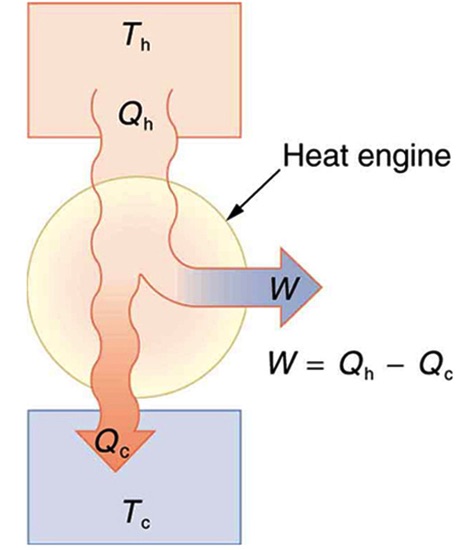
Let’s examine the four-stroke internal combustion gasoline engine of an automobile, shown in Figure 20.3, to see how a typical heat engine operates.
 |
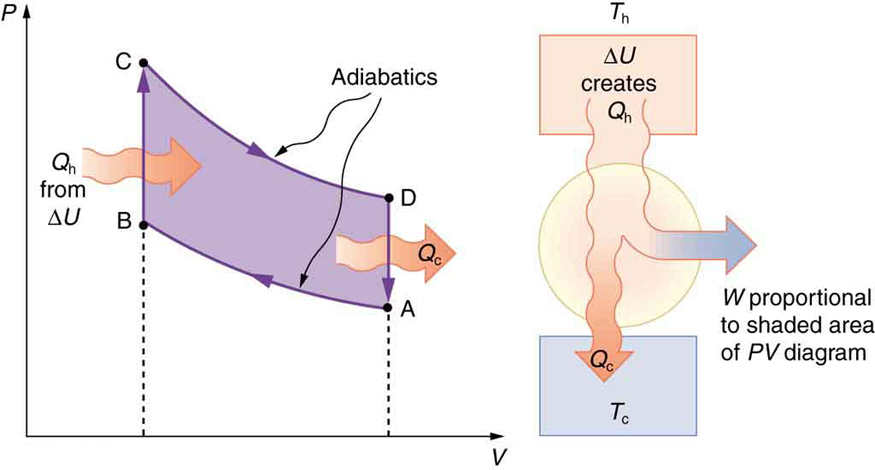 |
Figure 20.3(a) →Air is mixed with fuel during the intake stroke. The air-fuel mixture is the substance that goes through various thermodynamic processes and is called the working substance of this heat engine.
Figure 20.3(b)→ During the compression stroke, the air-fuel mixture is rapidly compressed in a nearly adiabatic process, as the piston rises with the valves closed. Work is done on the gas. This is shown on the PV diagram in Figure 20.4 as process A→B.
Figure 20.4(c)→The power stroke has two distinct parts. First, the air-fuel mixture is ignited, converting chemical potential energy into thermal energy almost instantaneously, which leads to a great increase in pressure. This is the process B→C on the PV diagram. Then the piston descends, and the gas does work by exerting a force through a distance in a nearly adiabatic fashion shown as process C→D.
Figure 20.4(d) The exhaust stroke expels the hot gas to prepare the engine for another cycle, starting again with the intake stroke. This stage is the process D→A on the PV diagram. For an automobile engine, the cold reservoir is the surrounding air, and the heat released in the exhaust stroke is the pollution dumped in the environment.
The shaded area inside the cycle on the PV diagram is equal to the work done by the engine in one cycle.
Since the purpose of a heat engine is to do mechanical work (such as moving the piston that eventually leads to the rotation of tires in an automobile), it is desirable to convert as much heat energy as possible into mechanical work. In fact, it would be great if all the heat energy could be turned into mechanical work. But this is physically impossible to do, and the Second Law of Thermodynamics can help us understand why.
Heat engines consist of a working substance, such as a gas in a cylinder, that goes through a cyclical process to convert heat transfer into work. A cyclical process brings the working substance back to its original state at the end of every cycle. Since the initial state of the gas at the beginning of the cycle is the same as its final state at the end, the change in entropy of the gas is zero, ΔS=0. Now, let’s examine the change in entropy of the isolated system of a heat engine as a whole. As a whole, the isolated system of a heat engine consists of a hot reservoir, the working substance of the heat engine, and the cold reservoir. As we discussed before, and numerically showed in Example 20.1, when heat leaves the hot reservoir, the entropy of the reservoir goes down. This means that if 100% of the heat energy leaving the hot reservoir was turned into work by the working substance of the heat engine, and considering that ΔS=0 for the cyclical process of the working substance itself, then the overall entropy of the system (system=hot reservoir + working substance of heat engine + cold reservoir) would decrease. This is clearly against the Second Law of Thermodynamics and that’s why it is impossible to convert 100% of the heat transferred out of the hot reservoir into mechanical work. So, only some of the heat leaving the hot reservoir can be converted to mechanical work. The rest of it is dumped into the cold reservoir, increasing the entropy of that reservoir (as shown in Example 20.1), so that the overall change in entropy of the system (the two reservoirs and the working substance of the heat engine) is positive and consistent with the Second Law of Thermodynamics.
the efficiency of a heat engine
The efficiency of a heat engine is defined as the ratio of the work done by the working substance to the heat transferred from the hot reservoir.
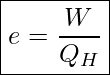 Efficiency Of A Heat Engine
Efficiency Of A Heat Engine
Since after one cycle, the working substance returns to its initial state, the change in its internal energy is zero, ΔU=0. If we apply the First Law of Thermodynamics (conservation of energy) to one cycle of the working substance we get
![]()
In one cycle, heat transferred into the working substance is QH, and heat leaving the working substance is Qc. Therefore
![]()
![]()
Now we can express efficiency in terms of QH and QC only.
![]()
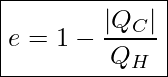 Efficiency Of A Heat Engine
Efficiency Of A Heat Engine
If it was physically possible to make QC=0, then we would end up with an efficiency of 1 or 100% for the heat engine. But, as we just discussed, the Second Law of Thermodynamics tells us that QC can never be zero. So, the question becomes how small can QC get and still not violate the Second Law? Alternatively, what maximum amount of work is physically possible to get from a heat engine that operates between two reservoirs with temperatures TH and TC?
To answer this question, first, notice that the amount of work produced in one cycle of a heat engine is represented by the enclosed area on the PV diagram. The larger the difference between the temperature of the two reservoirs, the greater the area. This idea is demonstrated in Figure 20.5. If the starting temperature of path CD is higher and the starting temperature of path AB is lower, the enclosed area, and therefore work done in one cycle is greater.
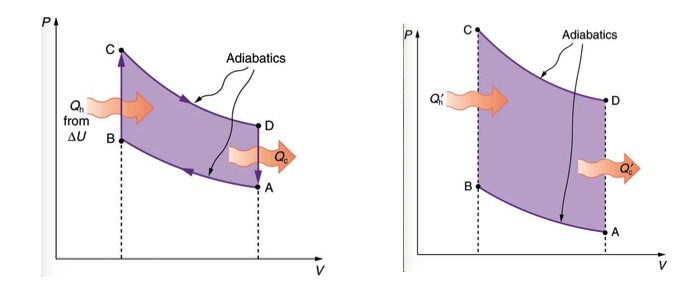
In 1824, french engineer Sadi Carnot proved that ideally, the most efficient cyclic process between any two given max and min temperatures, TH and TC, is made of two reversible isothermal, and two reversible adiabatic processes. This ideal cyclic process, which is also known as Carnot Cycle is shown in Figure 20.6
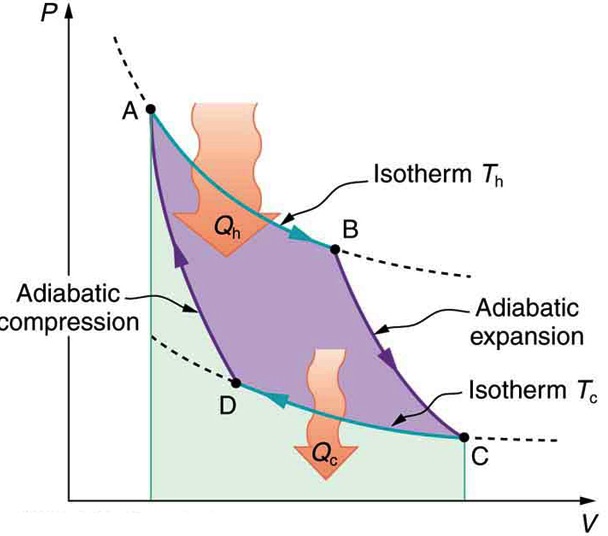
Carnot also showed that the efficiency of this ideal engine can be calculated with
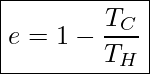 Efficiency Of An Ideal Carnot Engine
Efficiency Of An Ideal Carnot Engine
In this equation, both TH and TC are in Kelvin.
This is important because it puts a limit on how high the actual efficiency of a real engine that operates between temperatures of TC and TH can get. Anything higher than the efficiency of an ideal Carnot engine is physically impossible to achieve.
Example 20.3
Is it possible to construct an engine that absorbs 5000J of heat from a hot reservoir at a temperature of 200°C, does 4000J of work, and releases 1000J of heat into a cold reservoir at a temperature of 20.0°C?
Solution
In order to see if it’s physically possible to construct such an engine, we need to calculate the actual efficiency and compare that with the efficiency of an ideal engine that operates between the same two max and min temperatures. If the actual efficiency is less than the ideal efficiency, then it is physically possible to design and construct such an engine.
Actual efficiency of this engine is
![]()
![]()
![]()
Now, let’s calculate the ideal maximum efficiency.
![]()
We need to convert both temperatures to Kelvin.
![]() and
and ![]()
![]()
![]()
Since the actual efficiency is greater than the maximum efficiency that is physically possible, such an engine cannot exist.
Example 20.4
A lawnmower is rated to have an efficiency of 25.0% and an average power of 3.00 kW. What is
(a) the average work in one minute of use?
(b) the minimum heat discharged into the air by the lawnmower in one minute of use?
Solution for (a)
Power is how fast work is done. We can use power to find work done in one minute.
![]()
![]()
![]()
Solution for (b)
The efficiency of the lawn mower is 25.0%. Therefore
![]()
![]()
![]()
Now we can find QC which is the heat discharged into the air in one minute.
![]()
![]()
![]()
thermal pumps
A thermal pump is a device in which work is done to transfer heat from somewhere cold to somewhere hot. In essence, a thermal pump is a heat engine operating in reverse. Figure 20.7 is a schematic diagram of a thermal pump.

Thermal pumps are either refrigerators or heat pumps, depending on what the device is used for. If the purpose of the thermal pump is to remove heat from somewhere cold, we call it a refrigerator. But if the purpose is to transfer heat to somewhere warm, we call it a heat pump. Let’s examine the operation of a refrigerator to gain insight into how a thermal pump works.
Figure 20.8 is a diagram of a typical refrigerator. Figure 20.9 is a simplified diagram. The working substance is the fluid that runs through the pipes and is called a refrigerant or a coolant. In Figure 20.8, a coolant with a boiling temperature below the freezing point of water is sent through the cycle (clockwise in this diagram). When the liquid coolant runs through the evaporator (the section of pipes inside the refrigerator-See Figure 20.8) it absorbs heat from inside the refrigerator, goes through a phase change, and turns into gas. A compressor, outside of the refrigerator, compresses the gas. This high-pressure vapor goes through a condenser where it releases heat as it goes through another phase change and turns into a liquid. The liquid is sent back into the refrigerator and the cycle repeats.
The cold reservoir is the space inside the refrigerator at temperature TC, and the heat absorbed by the coolant to go through (liquid →gas) phase change is QC. The work, W, is done by the compressor. The hot reservoir at temperature TH is the space around the refrigerator where the heat released from the coolant’s phase change (gas →liquid) is dumped.
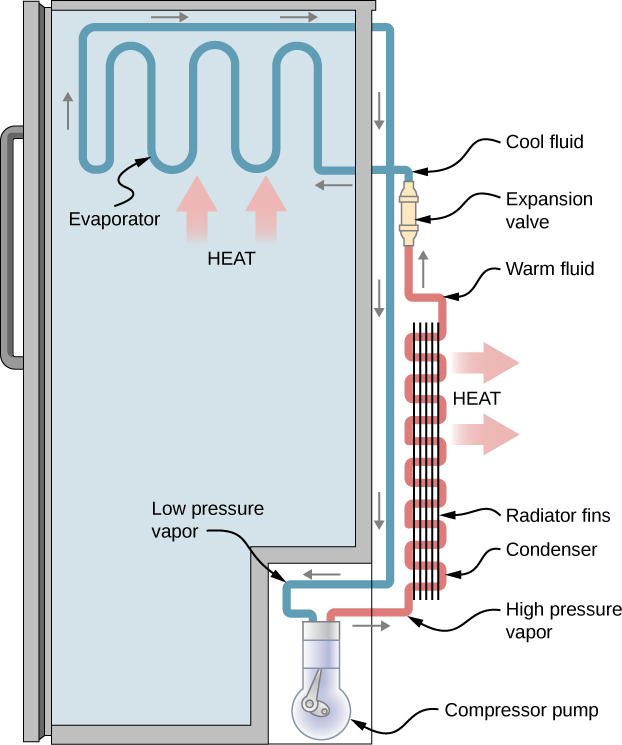 |
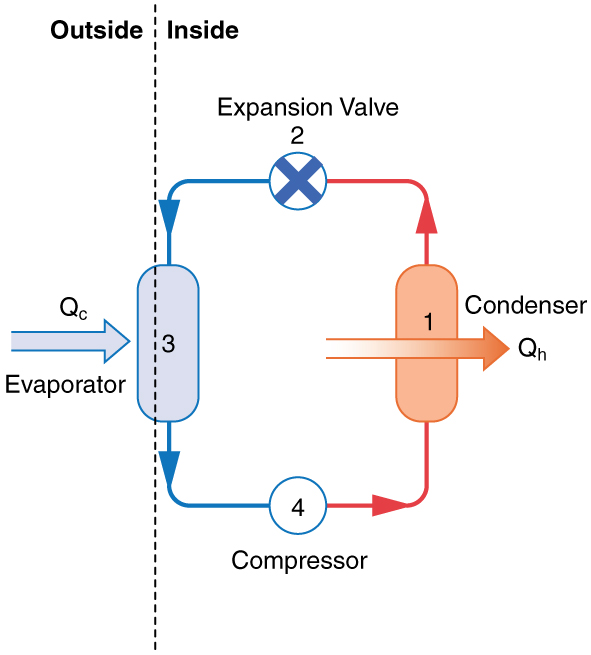 |
Just as a refrigerator is used to keep the cold reservoir cold, a heat pump is used to keep a hot reservoir warm. For example, the same device can be used to warm a house in winter. In that case, the cold reservoir would be outdoors, and the hot reservoir would be inside the house.
In summary, the function of a thermal pump is to force heat energy to flow from a cool body to a warm one at the expense of some input work.
The effectiveness of a refrigerator or a heat pump is indicated by their coefficient of performance as defined below.

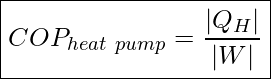
The coefficient of performance is the ratio of useful heating or cooling to work (energy) required. Like a heat engine, the operation of a thermal pump is cyclic, and therefore the change in internal energy of the working substance in one cycle is zero, ΔU=0. Applying the First Law of Thermodynamics (conservation of energy) to one cycle, we see that ![]()
Since ![]() , and the work is done on the gas, and therefore negative (W<0), we get
, and the work is done on the gas, and therefore negative (W<0), we get ![]() . Therefore, the COP’s can also be written in terms of QC and QH alone.
. Therefore, the COP’s can also be written in terms of QC and QH alone.
![]()
![]()
The great advantage of using a heat pump to keep your home warm, rather than just burning fuel, is that a heat pump supplies ![]() . Heat transfer is from the outside air, even at a temperature below freezing, to the indoor space. You only pay for |W|, and you get an additional heat transfer of |QC| from the outside at no cost; in many cases, at least twice as much energy is transferred to the heated space as is used to run the heat pump. When you burn fuel to keep warm, you pay for all of it. The disadvantage is that the work input (required by the second law of thermodynamics) is sometimes more expensive than simply burning fuel, especially if the work is done with electrical energy.
. Heat transfer is from the outside air, even at a temperature below freezing, to the indoor space. You only pay for |W|, and you get an additional heat transfer of |QC| from the outside at no cost; in many cases, at least twice as much energy is transferred to the heated space as is used to run the heat pump. When you burn fuel to keep warm, you pay for all of it. The disadvantage is that the work input (required by the second law of thermodynamics) is sometimes more expensive than simply burning fuel, especially if the work is done with electrical energy.
Similar to heat engines, it is possible to determine the maximum, physically possible values for the coefficient of performance of a thermal pump. These ideal COP’s are given by

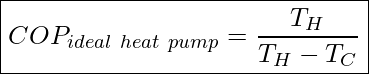
Example 20.5
A heat pump used to warm a home must employ a cycle that produces a working fluid at temperatures greater than typical indoor temperature so that heat transfer to the inside can take place. Similarly, it must produce a working fluid at temperatures that are colder than the outdoor temperature so that heat transfer occurs from outside. Its hot and cold reservoir temperatures therefore cannot be too close, placing a limit on its COP. What is the best coefficient of performance possible for such a heat pump, if it has a hot reservoir temperature of 45.0ºC and a cold reservoir temperature of -15.0ºC?
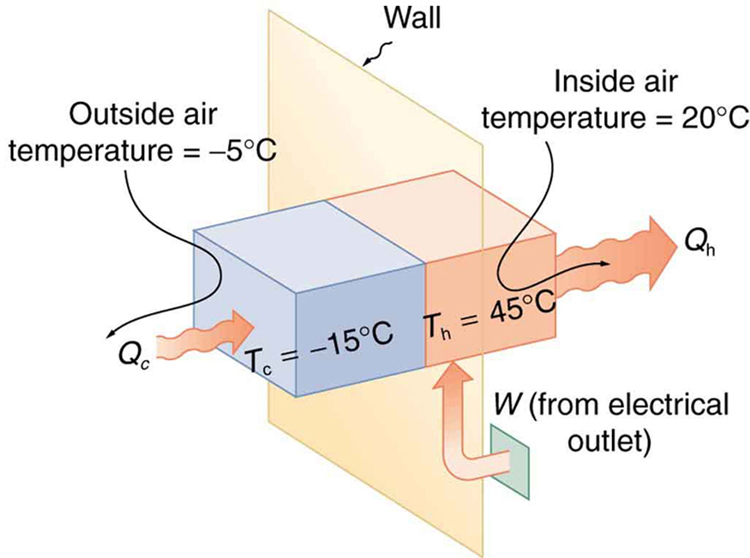
Solution
The COP of an ideal heat pump is given by
![]()
Let’s first convert temperatures to Kelvin.
TH=45.0+273=318K, and TC=-15.0+273=258K
![]()
![]()
Discussion
Since the COP of any heat pump is ![]() , in this case, we get
, in this case, we get
![]() or
or ![]() . This result means that the heat transfer by the heat pump is 5.30 times as much as the work put into it. It would cost 5.30 times as much for the same heat transfer by an electric room heater as it does for that produced by this heat pump.
. This result means that the heat transfer by the heat pump is 5.30 times as much as the work put into it. It would cost 5.30 times as much for the same heat transfer by an electric room heater as it does for that produced by this heat pump.
Attribution
This chapter contains material taken from Openstax College Physics-Thermodynamics, and Openstax University Physics Volume 2-The Second Law of Thermodynamics and is used under a CC BY 4.0 license. Download these books for free at Openstax
The section on The Second Law of Thermodynamics and Living Organisms is adapted from Openstax Biology, 2e. Access this book for free at https://openstax.org/books/anatomy-and-physiology/pages/1-introduction
To see what was changed, refer to the List of Changes.
questions and problems
questions
- For each process described below, indicate whether the entropy of the system increases, stays constant, or decreases. In each case, the system consists of the substance only.
- Water freezes into ice.
- Water boils and generates steam.
- In the system below, a hole is punctured in the partition and the gas expands and occupies the full container.

- A sugar cube is dissolved in water. (the system consists of sugar and water)
- A plant or any other living organism growing.
- soft drink cooling down in the refrigerator.
- In the previous question, in some of the processes, the entropy of the system was decreased. How is that consistent with the Second Law of Thermodynamics?
- A system consists of two substances at two different temperatures. Show that when heat is transferred from the hot substance to the cooler one, the entropy of the system increases.
- How is entropy related to the energy that is available to do work?
- What is a heat engine? Describe the general operation of a typical heat engine.
- What is a thermal pump? Describe the general operation of a typical thermal pump. Explain the difference between a heat pump and a refrigerator.
- The coefficient of performance of a thermal pump is always greater than 1. What does this mean?
problems
- [openstax college physics – 15.53] What is the decrease in entropy of 25.0 g of water that condenses on a bathroom mirror at a temperature of35.0°C assuming no change in temperature and given the latent heat of vaporization to be 2450 kJ/kg?
- [openstax univ. phys. vol. 2 – 2.47] The Sun radiates energy at the rate of 3.80×1026W from its 5500ºC surface into dark empty space (a negligible fraction radiates onto Earth and the other planets). The effective temperature of deep space is-270ºC. What is the increase in entropy in one day due to this heat transfer?
- Thirty (30.0) grams of milk at 10.0°C is added to 400g of coffee at 98.0°C in a well-insulated cup. Approximate the change in entropy of the system as it reaches equilibrium temperature. Take the specific heat of milk and coffee to be the same as water.
- [openstax univ. phys. vol.2 – 4.22] An engine is found to have an efficiency of 0.400. If it does 200 J of work per cycle, what are the corresponding quantities of heat absorbed and discharged?
- [openstax univ. phys. vol. 2 – 4.24] An engine with an efficiency of 0.300 absorbs 500 J of heat per cycle.
- How much work does it perform per cycle?
- How much heat does it discharge per cycle?
- [openstax univ. phys. vol. 2 – 4.27] An engine absorbs three times as much heat as it discharges. The work done by the engine per cycle is 50.0 J.
- Calculate the efficiency of the engine.
- Calculate the heat absorbed per cycle, and the heat discharged per cycle.
- [openstax univ. phys. vol. 2 – 4.29] A refrigerator has a coefficient of performance of 3.00.
- If it requires 200 J of work per cycle, how much heat per cycle does it remove from the cold reservoir?
- How much heat per cycle is discarded to the hot reservoir?
- [openstax univ. phys. vol. 2 – 4.31] A refrigerator discards 80.0 J of heat per cycle and its coefficient of performance is 6.00.
- How much heat does it remove per cycle from a cold reservoir?
- How much work per cycle is required for its operation?
- [openstax college physics – 15.41] A heat pump that has a hot reservoir temperature of 50.0ºC and a cold reservoir temperature of-20.0ºC.
- What is the maximum coefficient of performance this heat pump can have?
- How much heat transfer occurs into the warm environment if 3.60×107J of work is put into it?
- If the cost of this work input is 10.0 cents/kWh, how does this cost compare with the cost of direct heat transfer achieved by burning natural gas at 85.0 cents per therm? (A therm is a common unit of energy for natural gas and equals 1.055×108J )
- [openstax college physics – 15.44] An ideal heat pump is being considered for use in heating an environment with a temperature of 22.0ºC. What is the cold reservoir temperature if the pump is to have a coefficient of performance of 12.0?
- 8000J of work is done to isothermally compress an ideal gas that is at 0ºC. Does the entropy of the gas increase, decrease, or stay the same in this process? Explain your reasoning and calculate the change in entropy.
- For each process below, determine the change in entropy and explain why your answer does not violate the Second Law of Thermodynamics.
- 5.00g of ethanol freezes.
- 5.00g of copper melts.
- [openstax college phys. 15.16] Is it possible for a heat engine to do 4.00kJ of work on an input of 24.0kJ of heat transfer while 16.0kJ of heat transfers to the environment? Justify your answer.
- [openstax college phys. 15.46] Show that the coefficients of performance of refrigerators and heat pumps are related by COPref=COPhp-1
- [openstax college phys. 15.47] On a winter day, a certain house loses 5.00×108J of heat to the outside. What is the total change in entropy due to this heat transfer alone, assuming an average indoor temperature of 21.0°C and an average outdoor temperature of 5.00°C?
- [openstax college phys. 15.66]A Carnot refrigerator exhausts heat to the air, which is at a temperature of 25.0°C. How much power is used by the refrigerator if it freezes 1.5g of water per second? Assume the water is at 0°C.
