Kinematics – Motion in Two Dimensions
Unit 5 – Projectile Motion and Circular Motion
Last Update: 5/14/2025
kinematics of projectile motion
Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, such as that of a football or other object for which air resistance is negligible. The following simulation shows a ball being projected below horizontal, horizontally, and at angles above the horizontal.
The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. This choice of axes is the most sensible because the acceleration due to gravity is vertical—thus, there will be no acceleration along the horizontal axis when air resistance is negligible. As is customary, we call the horizontal axis the x-axis and the vertical axis the y-axis.
The following steps are then used to analyze projectile motion:
Step 1. Resolve or break the motion into horizontal and vertical components along the x- and y-axes.
Step 2. Treat the motion as two independent one-dimensional motions, one horizontal with constant velocity and the other vertical with constant acceleration.
The kinematic equations for horizontal and vertical motion take the following forms:
Horizontal Motion – The x-component of velocity is constant (Vx = V0x = constant)
![]()
Vertical Motion – Acceleration is due to gravity and therefore constant (ay = 9.8m/s2 ↓)
![]()
![]()
![]()
![]()
Step 3. Solve for the unknowns in the two separate motions—one horizontal and one vertical. Note that the only common variable between the motions is time, t.
Step 4. Recombine the two motions to find the total displacement and the total velocity at any point along the trajectory.
Figure 5.1 shows how we analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. The horizontal motion is simple because the horizontal component of the velocity does not change. In the vertical direction, the acceleration is due to gravity and therefore constant and downward at all times. This means that while the object is moving up, its velocity in the y-direction decreases at a rate of 9.8m/s every second, and while it is moving down, this velocity increases at a rate of 9.8m/s every second.
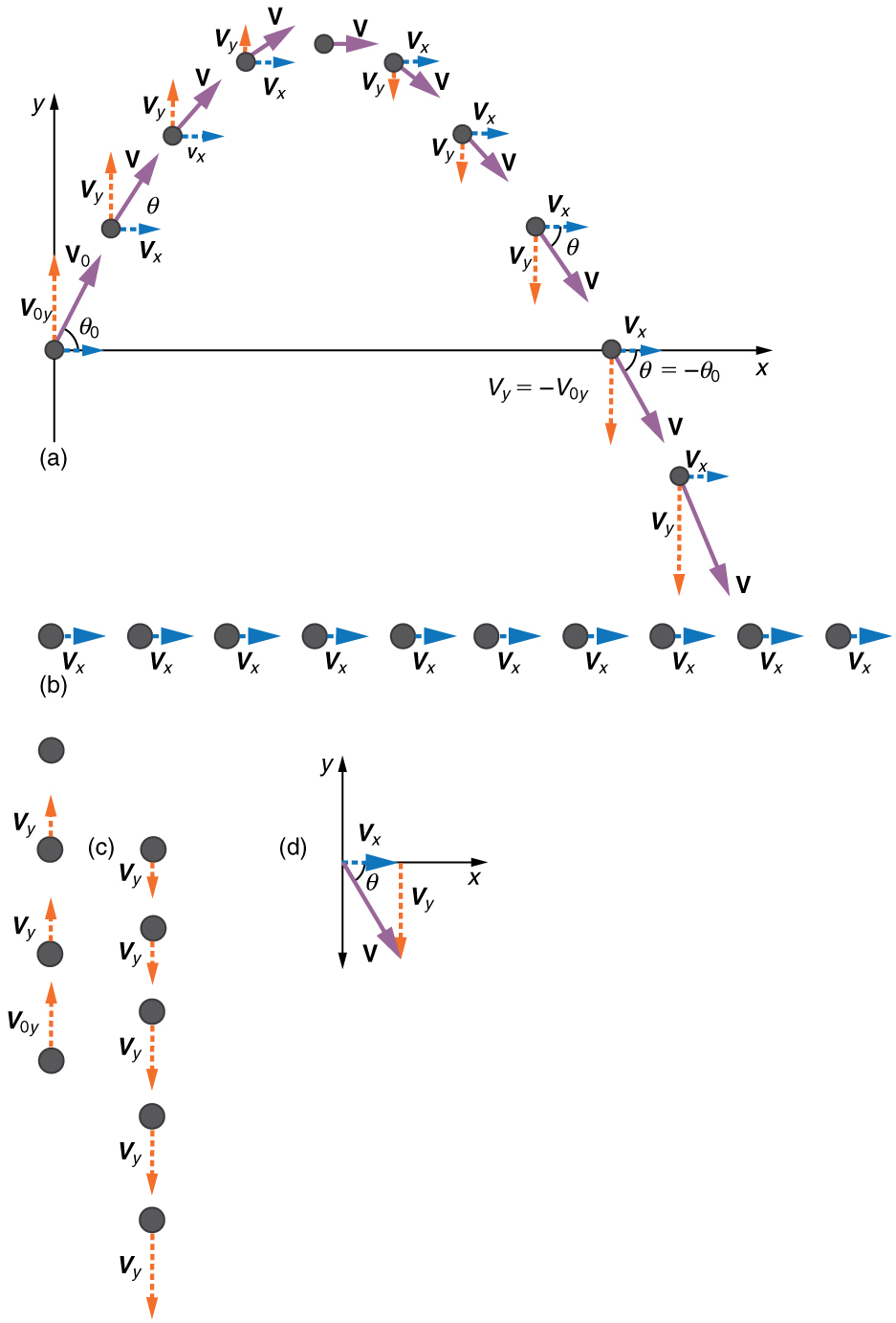
It is important to set up a coordinate system when analyzing projectile motion. One part of defining the coordinate system is to define an origin for the x and y positions. Often, it is convenient to choose the initial position of the object as the origin such that x0=0 and y0=0. It is also important to define the positive and negative directions in the x and y directions. Typically, we define the positive vertical direction as upwards, and the positive horizontal direction is usually the direction of the object’s motion. When this is the case, the vertical acceleration, acceleration due to gravity, takes a negative value (since it is directed downwards towards the center of the Earth). However, it is occasionally useful to define the coordinates differently. For example, if you are analyzing the motion of a ball thrown downwards from the top of a cliff, it may make sense to define the positive direction downwards since the motion of the ball is solely in the downwards direction. If this is the case, the vertical acceleration, acceleration due to gravity, takes a positive value.
A fundamental concept to remember when analyzing projectile motion is that the velocities in the horizontal and vertical directions are completely independent of one another. In other words, the horizontal and vertical parts of the motion are two independent motions that occur at the same time. One way to demonstrate this is to compare the time in the air of a bullet that is dropped from a certain height with the time in the air of a bullet that is fired horizontally from the same height. Since the fired bullet leaves the gun horizontally, its initial velocity in the vertical direction is zero, just like the initial velocity of the dropped bullet. If the vertical and horizontal motions are truly independent, then we should expect both bullets to hit the ground at the same time. Do they? Let’s watch this Myth Busters video and find out.
Notice that even with air resistance it takes practically the same amount of time for the two bullets to reach the ground. In this book, we will ignore the effect of air resistance on all projectile motions unless stated explicitly otherwise.
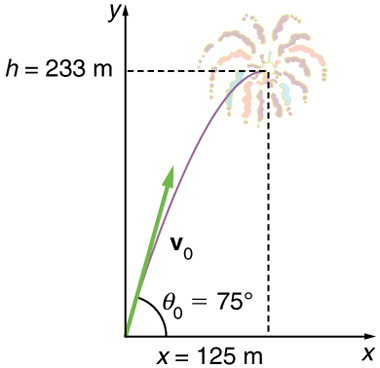
Example 5.1 – A Fireworks Projectile Explodes High And Away
During a fireworks display, a shell is shot into the air with an initial speed of 70.0 m/s at an angle of 75.0º above the horizontal, as illustrated below. The fuse is timed to ignite the shell just as it reaches its highest point above the ground.
(a) Calculate the height at which the shell explodes.
(b) How much time passed between the launch of the shell and the explosion?
(c) What is the horizontal displacement of the shell when it explodes?
Strategy
Because air resistance is negligible for the unexploded shell, the analysis method outlined above can be used. The motion can be broken into horizontal and vertical motions in which ax=0 and ay=9.8m/s2 ↓. We can then define x0=0 and y0=0 at the starting point and solve for the desired quantities.
Solution for (a)
By “height”, we mean the altitude or vertical position y above the starting point. The highest point in any trajectory, called the apex, is reached when vy=0. If we take the initial position to be the starting point and the final position to be the apex, we know the initial and final velocities as well as the initial position, and we can use the following equation to find the final position y:
![]()
Let’s take “up” to be the positive direction.
Now we must find v0y, the component of the initial velocity in the y-direction.
![]()
![]()
![]()
![]()
Since we also know y0 =0 and vy=0, and ay=-9.8m/s2, we can now solve for y.
![]()
![]()
Discussion for (a)
Note that because up is positive, the initial velocity is positive, as is the maximum height, but the acceleration due to gravity is negative. Note also that the maximum height depends only on the vertical component of the initial velocity so that any projectile with a 67.6 m/s initial vertical component of velocity will reach a maximum height of 233 m (neglecting air resistance). The numbers in this example are reasonable for large fireworks displays, the shells of which do reach such heights before exploding. In practice, air resistance is not completely negligible, and so the initial velocity would have to be somewhat larger than that given to reach the same height.
Solution for (b)
As in many physics problems, there is more than one way to solve for the time to the highest point. In this case, the easiest method is to use
![]()
Since at the top, vy=0
![]()
![]()
Discussion for (b)
This time is also reasonable for large fireworks. When you are able to see the launch of fireworks, you will notice several seconds pass before the shell explodes.
Solution for (c)
Because air resistance is negligible, the horizontal velocity is constant, as discussed above. We can find the horizontal velocity by calculating the x-component of the initial velocity.
![]()
![]()
![]()
![]()
We also know x0=0, and now we can solve for the horizontal displacement.
![]()
![]()
![]()
Discussion for (c)
The horizontal motion is a motion with constant velocity in the absence of air resistance. The horizontal displacement found here could be useful in keeping the fireworks fragments from falling on spectators. Once the shell explodes, air resistance has a major effect, and many fragments will land directly below.
Video Example – Ball kicked from the ground level
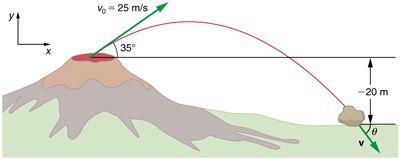
Example 5.2 – Calculating Projectile Motion: Hot Rock Projectile
Kilauea in Hawaii is the world’s most continuously active volcano. Very active volcanoes characteristically eject red-hot rocks and lava rather than smoke and ash. Suppose a large rock is ejected from the volcano with a speed of 25.0 m/s and at an angle 35.0º above the horizontal, as shown below. The rock strikes the side of the volcano at an altitude 20.0 m lower than its starting point.
(a) Calculate the time it takes the rock to follow this path.
(b) What are the magnitude and direction of the rock’s velocity at impact?
Strategy
Again, resolving this two-dimensional motion into two independent one-dimensional motions will allow us to solve for the desired quantities. The time a projectile is in the air is governed by its vertical motion alone. We will solve for t first. While the rock is rising and falling vertically, the horizontal motion continues at a constant velocity. This example asks for the final velocity. Thus, the vertical and horizontal results will be recombined to obtain the magnitude and direction of the velocity at the final time t determined in the first part of the example.
Solution for (a)
While the rock is in the air, it rises and then falls to a final position 20.0 m lower than its starting altitude. We can find the time for this by using
![]()
If we take the initial position y0=0, then the final position is y =-20.0m. Now the initial vertical velocity is the y- component of the initial velocity.
![]()
![]()
![]()
Substituting known values yields
![]()
Rearranging terms gives a quadratic equation in t.
![]()
This equation is in the form of ![]() which is solved by using the quadratic formula
which is solved by using the quadratic formula![]()
Applying the quadratic formula yields:
![]()
![]() and
and ![]()
The negative value of time implies an event before the start of motion, and so we discard it. Thus, ![]()
Discussion for (a)
The time for projectile motion is completely determined by the vertical motion. So any projectile that has an initial vertical velocity of 14.3 m/s and lands 20.0 m below its starting altitude will spend 3.96 s in the air.
Solution for (b)
From the information now in hand, we can find the horizontal and vertical components of the final velocity, vx and vy, and combine them to find the total velocity and the angle it makes with the horizontal. Of course, vx is constant so we can solve for it at any horizontal location. In this case, we chose the starting point since we know both the initial velocity and initial angle. Therefore:
![]()
![]()
![]()
The final vertical velocity can be calculated by the following equation:
![]()
![]()
![]()
To find the magnitude of the final velocity from its components, we can use the Pythagorean theorem, which gives
![]()
![]()
The direction of the final velocity is determined by calculating the angle the velocity makes with the horizontal, Θ.
![]()
![]()
![]()
Therefore, the final velocity at the moment of impact is
![]()
Discussion for (b)
The negative angle means that the velocity is below the horizontal. This result is consistent with the fact that the final vertical velocity is negative and hence downward—as you would expect because the final altitude is 20.0 m lower than the initial altitude.
Video Example – Object released from a diving airplane
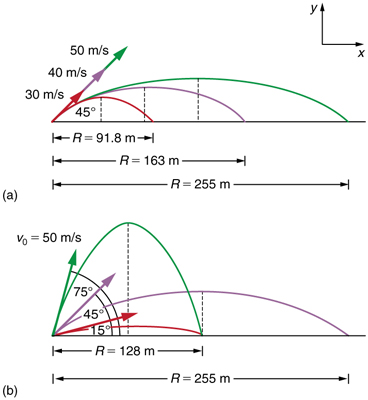
How does the initial velocity of a projectile affect its range? Obviously, the greater the initial speed, the greater the range, as shown in Figure 5.2(a). The initial angle θ also has a dramatic effect on the range, as illustrated in Figure 5.2(b). For a fixed initial speed, such as might be produced by a cannon, the maximum range is obtained with θ0=45º size. This is true only for conditions neglecting air resistance. Interestingly, for every initial angle except 45º, there are two angles that give the same range—the sum of those angles is 90º size.
Example 5.3
A tennis player wins a match at Arthur Ashe stadium and hits a ball into the stands at 30.0 m/s and at an angle 45º above the horizontal. On its way down, the ball is caught by a spectator 10.0 m above the point where the ball was hit.
(a) Calculate the time it takes the tennis ball to reach the spectator.
(b) What are the magnitude and direction of the ball’s velocity at impact?
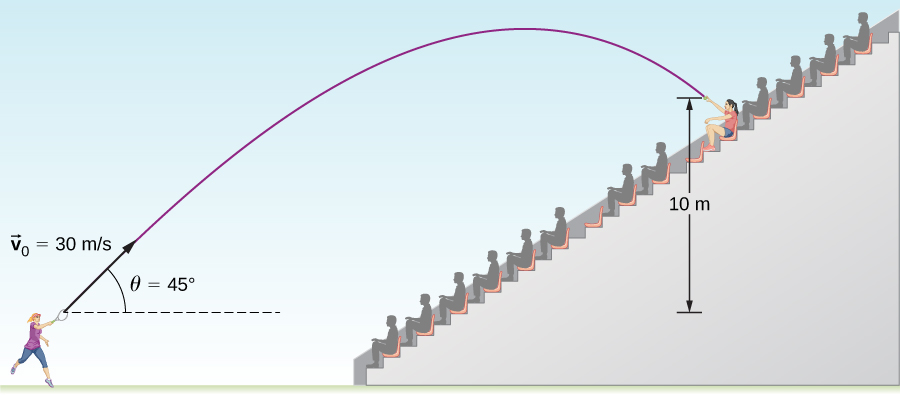
Solution for (a)
The time a projectile is in the air is governed by its vertical motion alone. We need to first find the vertical component of the initial velocity and then use the vertical part of the motion to determine the time it takes the ball to reach a position 10m above its starting point on its way down.
![]()
![]()
![]()
Now we can find the time the ball is in the air by using
![]()
We take the origin to be where the ball is released.
![]()
Rearranging this we get a quadratic equation.
![]()
The solutions are: t=3.79s, and t=0.54s. The smaller value, t-0.54s is the time it takes the ball to reach a height of 10.0m on its way up, and the longer time, t=3.79s is the time it takes to reach the same height on its way down. Notice that the time for projectile motion is determined completely by the vertical motion. Thus, any projectile that has an initial vertical velocity of 21.2 m/s and lands 10.0 m below its starting altitude spends 3.79 s in the air.
Solution for (b)
The ball’s horizontal component of the velocity does not change. We can determine this component by using the initial velocity.
![]()
![]()
![]()
Now let’s find the vertical component of the velocity at the instant the ball is caught.
![]()
![]()
![]()
So, at the moment the ball is caught, its velocity is ![]() .
.
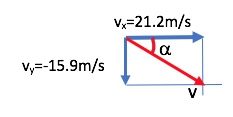
Now let’s use the Pythagorean theorem to find the magnitude of the velocity.
![]()
![]()
To find the direction, we calculate the angle between the velocity vector and the horizontal line, θ.
![]()
![]()
![]()
So, at the moment the ball is caught, its velocity is ![]()
Kinematics of uniform circular motion
We know from kinematics that acceleration is a change in velocity, either in its magnitude or in its direction, or both. In a uniform circular motion, the direction of the velocity changes constantly, so there is always an associated acceleration, even though the magnitude of the velocity might be constant. You experience this acceleration yourself when you turn a corner in your car. (If you hold the wheel steady during a turn and move at a constant speed, you are in a uniform circular motion.) What you notice is a sideways acceleration because you and the car are changing direction. The sharper the curve and the greater your speed, the more noticeable this acceleration will become. In this section, we examine the direction and magnitude of that acceleration.
Figure 6.1 shows an object moving in a circular path at a constant speed. The direction of the instantaneous velocity is shown at two points along the path. Acceleration is in the direction of the change in velocity, which points directly toward the center of rotation (the center of the circular path). This pointing is apparent in the vector diagram in Figure 6.1. Notice that since the direction of velocity continuously changes, in order to find the direction of ![]() at a given instant, we need to subtract initial and final velocities that are infinitely close to one another. The velocities
at a given instant, we need to subtract initial and final velocities that are infinitely close to one another. The velocities ![]() and
and ![]() in Figure 6.1 are significantly apart to make the diagram more clear, but if they were truly infinitely close to one another, then the vector
in Figure 6.1 are significantly apart to make the diagram more clear, but if they were truly infinitely close to one another, then the vector ![]() would point exactly toward the center of the circular path. We call the acceleration of an object moving in a uniform circular motion, the centripetal acceleration. Centripetal means “toward the center” or “center seeking.”
would point exactly toward the center of the circular path. We call the acceleration of an object moving in a uniform circular motion, the centripetal acceleration. Centripetal means “toward the center” or “center seeking.”
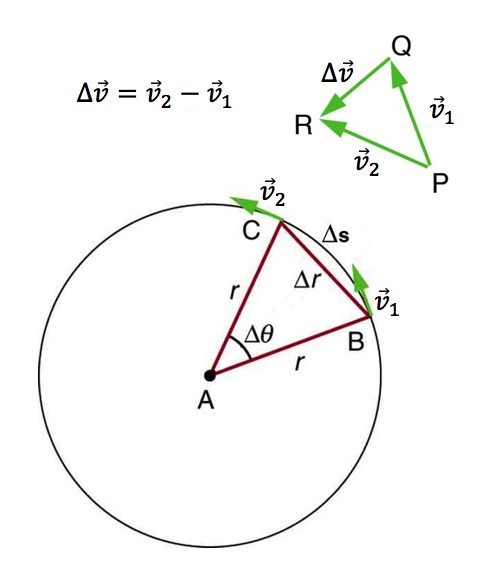
The direction of centripetal acceleration is toward the center of the circular path, but what is its magnitude? Note that the triangle formed by the velocity vectors and the one formed by the radii r and Δs are similar. Once again, when ![]() and
and ![]() are infinitely close to one another, Δs and Δr become practically the same. Both the triangles ABC and PQR are isosceles triangles (two equal sides). The two equal sides of the velocity vector triangle are the speeds
are infinitely close to one another, Δs and Δr become practically the same. Both the triangles ABC and PQR are isosceles triangles (two equal sides). The two equal sides of the velocity vector triangle are the speeds ![]() and
and ![]() . Using the properties of two similar triangles, we obtain
. Using the properties of two similar triangles, we obtain
![]()
Magnitude of acceleration is ![]() , and so we first solve this expression for
, and so we first solve this expression for ![]()
![]()
Then we divide this by Δt, yielding
![]()
Finally, noting that ![]() and that
and that ![]() , we see that the magnitude of the centripetal acceleration is
, we see that the magnitude of the centripetal acceleration is
![]()
 Centripetal Acceleration
Centripetal Acceleration
ac is the acceleration of an object in a circle of radius r at a speed v. So, centripetal acceleration is greater at high speeds and in sharp curves (smaller radius), as you have noticed when driving a car. But it is a bit surprising that ac is proportional to speed squared, implying, for example, that it is four times as hard to take a curve at 100 km/h than at 50 km/h. A sharp corner has a small radius so that ac is greater for tighter turns, as you have probably noticed.
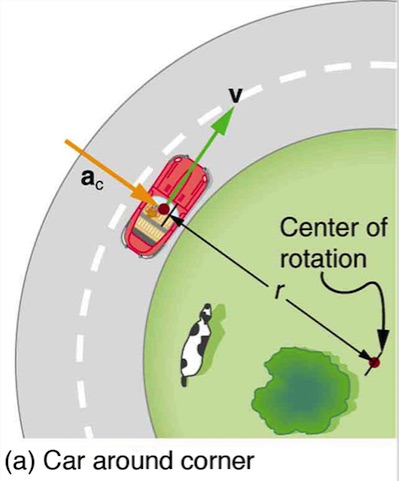
Example 5.4 – How Does The Centripetal Acceleration Of A Car Around A Curve Compare With That Due To Gravity?
What is the magnitude of the centripetal acceleration of a car following a curve of radius 500 m at a speed of 25.0 m/s (about 90 km/h)? Compare the acceleration with that due to gravity for this fairly gentle curve taken at highway speed.
Strategy
The car following a circular path at constant speed is accelerated perpendicular to its velocity, as shown in Figure 6.2(a) . The magnitude of this centripetal acceleration is found by using
![]()
Solution
Entering the given values of v=25.0m/s and r=500m into this expression gives
![]()
![]()
Discussion
To compare this with the acceleration due to gravity, g=9.8 m/s2, we take the ratio of the two accelerations:
![]()
Thus ac = 0.128g. This is noticeable especially if you were not wearing a seat belt.
Video Example – Circular motion of a ball attached to a string
Example 5.5 – How Big Is the Centripetal Acceleration In An Ultracentrifuge?
Calculate the centripetal acceleration of a point 7.50 cm from the axis of an ultracentrifuge spinning at 7.5×104 rev/min. Determine the ratio of this acceleration to that due to gravity.
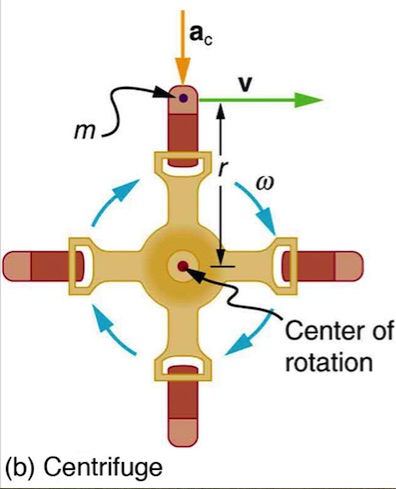
Strategy
A particle of mass in a centrifuge is rotating at constant angular velocity. It must be accelerated perpendicular to its velocity or it would continue in a straight line. See Figure 6.2(b). The magnitude of the necessary acceleration is found by using
![]()
Solution
The term rev/min stands for revolutions per minute. We can use this to find the speed of the particle in m/s. One revolution is a distance that is equal to the circumference of the circular path, 2πr. Therefore
![]()
Now the centripetal acceleration can be calculated.
![]()
![]()
Taking the ratio of ac to g yields
![]()
Discussion
This last result means that the centripetal acceleration is 472,000 times as strong as g. It is no wonder that centrifuges with such fast rotational speeds are called ultracentrifuges. The extremely large accelerations involved greatly decrease the time needed to cause the sedimentation of blood cells or other materials.
Attributions
This chapter contains material taken from Openstax College Physics-Kinematics in Two Dimensions and “Openstax College Physics-Uniform Circular Motion and Gravitation by Openstax and is used under a CC BY 4.0 license. Download this book for free at Openstax-College Physics
To see what was changed, refer to the List of Changes.
Questions and problems
Questions
- [openstax univ. phys. vol1] Answer the following questions fo r a projectile motion on level ground assuming negligible air resistance, with the initial angle being neither 0º nor 90°. For each question justify your answer.
- Is the velocity ever zero?
- When is the magnitude of the velocity at its minimum? at its maximum?
- Can the velocity vector ever be the same as the initial velocity vector at any instant other than at t=0?
- Can the magnitude of the velocity (speed) ever be the same as the magnitude of the initial velocity (initial speed) other than at t=0?
- Is the acceleration ever zero?
- Is the velocity vector ever parallel or anti-parallel to the acceleration vector?
- Is the velocity vector ever perpendicular to the acceleration vector?
- Explain the difference between the linear acceleration of an object moving along a straight line, and the centripetal acceleration of an object moving around a circular path.
- Draw a motion diagram for an object moving around a circular path in a counterclockwise direction at a constant speed.
- Use a round object like the lid of a jar to draw a perfect circle. Then use a ruler to draw two velocity vectors showing the velocities of an object moving around the circular path with constant speed. Draw the velocity vectors close to one another. Finally, use vector subtraction to find the direction of the centripetal acceleration, which is the same as the direction of
- [openstax-college physics 6.2] Can centripetal acceleration change the speed of circular motion? Explain.
Problems
- An object is projected with an initial velocity v0 from a height of 10.0m from the ground. Determine how long the object is in the air, the velocity with which it strikes the ground (magnitude and direction), and the horizontal distance traveled when it lands for the following cases.
- The initial velocity is horizontal and has a magnitude of 5.00m/s.
- The initial velocity is 5.00m/s at 30.0° above the horizontal.
- The initial velocity is 5.00m/s at 30.0° below the horizontal.
- [openstax univ. phys. vol. 1 – 4.39] A projectile is launched at an angle of 30º and lands 20.0 s later at the same height as it was launched.
- What is the initial speed of the projectile?
- What is the maximum altitude?
- What is the horizontal distance traveled?
- [openstax univ. phys. vol. 1 – 4.40] A basketball player shoots toward a basket 6.10 m away and 3.0 0m above the floor. If the ball is released 1.80 m above the floor at an angle of 60.0º above the horizontal, what must the initial speed be if it were to go through the basket?
- [openstax univ. phys. vol. 1 – 4.41] At a particular instant, a hot air balloon is 100 m in the air and descending at a constant speed of 2.00 m/s. At this exact instant, a girl throws a ball horizontally, relative to herself, with an initial speed of 15.0 m/s. When she lands, where will she find the ball?
- [openstax univ. phys. vol. 1 – 4.45] A rock is thrown off a cliff with a velocity of 30.0m/s at an angle of 53.0º with respect to the horizontal. The cliff is 100 m high.
- How high above the edge of the cliff does the rock rise?
- How far has it moved horizontally when it is at maximum altitude?
- How long after the release does it hit the ground?
- What is the horizontal distance traveled by the rock when it lands?
- What are the horizontal and vertical positions of the rock relative to the edge of the cliff at t = 4.00 s?
- [openstax univ. phys. vol. 1 – 4.46] Trying to escape his pursuers, a secret agent skis off a slope inclined at 30.0º below the horizontal at 60.0 km/h. To survive and land on the snow 100 m below, he must clear a gorge 60.0 m wide. Does he make it? Ignore air resistance.
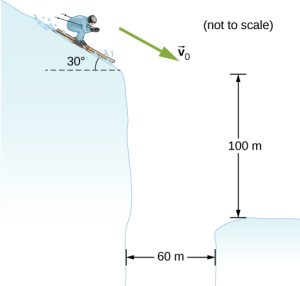
fig-prob5.6 - [openstax univ. phys. vol. 1 – 4.55] A soccer goal is 2.44 m high. A player kicks the ball at a distance of 10.0 m from the goal at an angle of 25.0º. The ball hits the crossbar at the top of the goal. What is the initial speed of the soccer ball?
- [openstax univ. phys. vol. 1 – 4.57] In 1999, Robbie Knievel was the first to jump the Grand Canyon on a motorcycle. At a narrow part of the canyon (69.0 m wide) and traveling 35.8 m/s off the takeoff ramp, he reached the other side. What was his launch angle? He landed at the same height that he left the ramp.
- [Jeffrey Schnick – SAC 110] A person throws a rock directly forward over flat, level ground. The rock leaves the thrower’s hand at a height of 1.67 m above ground level with a velocity of 14.2 m/s directed along the horizontal. How far forward does the rock go before it hits the ground?
- [Jeffrey Schnick – SAC 110] A person hits a golf ball over flat level ground directly toward a wall that is facing the golfer. The ball does hit the wall. The ball leaves the golf club at ground level from a point that is 52.0 m from the wall with a velocity of 33.0 m/s at an angle of 29.0° above the horizontal. How high up on the wall does the ball hit?
- [B. Crowell, B. Shotwell-modified] A baseball pitcher throws a pitch clocked at 33.0 m/s. He throws the ball horizontally.
- By what amount, d, does the ball drop by the time it reaches home plate, a distance of 18.3 m away?
- What is the magnitude and direction of the velocity of the ball when it is above the home plate?
- [Julio Gea-Banacloche-univ. phys1] A pitcher throws a fastball horizontally at a speed of 42.0m/s. Neglecting air resistance,
- How long does it take for the ball to reach the batter, a distance of 18.4m away?
- How much does the ball drop vertically in this time?
- What is the vertical component of the ball’s velocity as it reaches the batter?
- [Julio Gea-Banacloche-univ. phys1] A golf ball is hit in such a way that it travels 300m horizontally and stays in the air for a total of 6.00s. what was its initial velocity?
- [Openstax-univ. phys. vol1] An airplane flying horizontally with a speed of 500 km/h at a height of 800 m drops a crate of supplies (see the following figure). If the parachute fails to open, how far in front of the release point does the crate hit the ground?
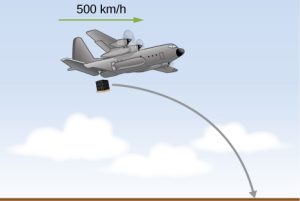
fig-prob5.14 [Image Description] - [Openstax-univ. phys. vol1] Mike Powell set the record for the long jump of 8.95m in 1991. If he left the ground at an angle of 20.0°, what was his initial speed?
- [Openstax-univ. phys. vol1] A soccer goal is 2.44m high. a player kicks the ball at a distance of 10.0m from the goal at an angle of 25.0°. The ball hits the crossbar at the top of the goal. what is the initial speed of the soccer ball?
- [openstax unv. phys. vol. 1 – 4.60] A flywheel is rotating at 30 rev/s. What is the total angle, in radians, through which a point on the flywheel rotates in 40 s?
- [openstax unv. phys. vol. 1 – 4.64] A runner taking part in the 200-m dash must run around the end of a track that has a circular arc with a radius of curvature of 30.0 m. The runner starts the race at a constant speed. If she completes the 200-m dash in 23.2 s and runs at a constant speed throughout the race, what is her centripetal acceleration as she runs the curved portion of the track?
- [openstax unv. phys. vol. 1 – 4.65] What is the acceleration of Venus toward the Sun, assuming a circular orbit? Hint: You need to look up the numbers you need.
- [openstax unv. phys. vol. 1 – 4.67] A fan is rotating at a constant 360.0 rev/min. What is the magnitude of the acceleration of a point on one of its blades 10.0 cm from the axis of rotation?
- [openstax unv. phys. vol. 1 – 4.68] A point located on the second hand of a large clock has a centripetal acceleration of 0.10cm/s2. How far is the point from the axis of rotation of the second hand?
- A ball is attached to the end of a rope and spun in a circle of radius 0.750m. The ball makes 0.900 revolutions per second. Find its centripetal acceleration in m/s2.
- A propeller plane with a speed of 170m/s makes a complete circular turn in a horizontal plane in 2.00 minutes.
- Find the radius of the circular path.
- Find the magnitude of the centripetal acceleration.
- The average distance between the Earth and the Sun is 1.50×1011m.
- Find the speed of the earth as it revolves around the Sun.
- Find the centripetal acceleration of the Earth.
- The radius of the Earth is 6.37×106m.
- Find the speed of a tree at the equator due to the Earth’s rotation.
- Find the centripetal acceleration of that tree.
Additional problems
Additional problems related to projectile motion are available online.
image Description
fig-prob5.14 image description – An airplane is shown flying. An arrow above it shows the velocity. A crate is right below the airplane. The trajectory of the crate is shown as a parabola. [Return to the image]
