Dynamics – Forces and Motion
Unit 6 – Newton’s Laws
Last Update: 5/23/2024
Newton’s laws of motion
Newton’s Laws of Motion are the cornerstones of a branch of physics called dynamics. Dynamics is the study of forces and their effect on the motion of objects. Newton’s Laws of Motion are:
Newton’s First Law of motion: A body at rest remains at rest or, if in motion, remains in motion at constant velocity unless acted on by a net external force.
Newton’s Second Law of motion: The acceleration of a body is directly proportional to and in the same direction as the net external force acting on the body and is inversely proportional to its mass. In equation form, Newton’s second law is ![]()
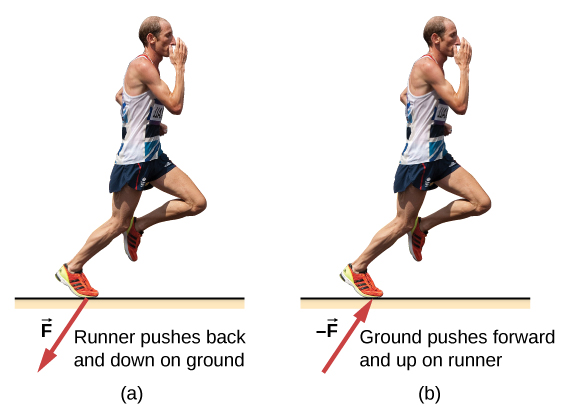
Newton’s Third Law of motion: Whenever one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that it exerts.
We have defined acceleration as the rate of change of velocity.
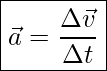 Definition of acceleration
Definition of acceleration
Newton’s Second Law of motion states the cause of acceleration. if an object experiences an unbalanced force, its motion will change such that the resulting acceleration is directly proportional to the net force and inversely proportional to the mass of the object. In short:
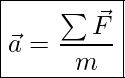 Cause of acceleration
Cause of acceleration
Newton’s First Law of motion states that all objects have an inherent resistance against change in their motion. This resistance is called inertia, and mass is a measure of inertia. The more massive an object is, the more inertia it has. It is obviously more difficult to change the motion of a large boulder than that of a basketball, for example. The inertia of an object is measured by its mass. Roughly speaking, mass is a measure of the amount of “stuff” (or matter) in something. The quantity or amount of matter in an object is determined by the number of atoms and molecules of various types it contains.
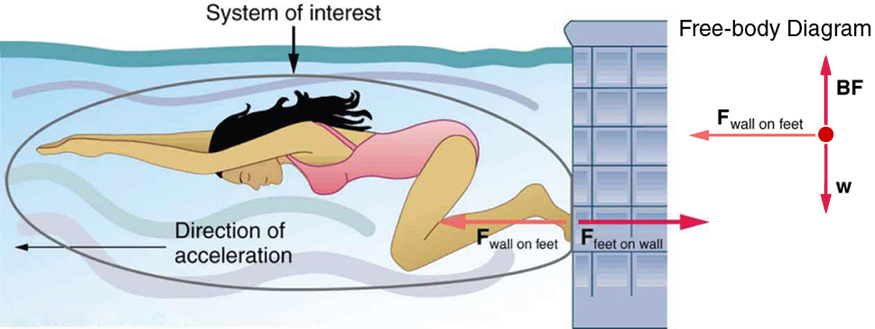
Newton’s Third Law defines force as an interaction between two objects. Therefore, every time we think about a force or try to identify forces involved in a given situation we must start by identifying the objects that are interacting. It takes two objects to interact, but there is only one interaction. This means the two interacting objects experience the same size force. Even though in most cases interaction requires physical contact, there are situations where two objects can interact (apply forces on each other) without coming into contact. Gravitational force is an example of such interaction. The gravitational force of the Earth acts on your body whether your feet are touching the ground or not.
We intuitively know that force, which is the result of interaction between two objects, manifests itself in the form of a push or pull. A push or pull has both magnitude and direction (therefore, it is a vector quantity) and can vary considerably in each regard. For example, a cannon exerts a strong force on a cannonball that is launched into the air. In contrast, Earth exerts only a tiny downward pull on a flea. Our everyday experiences also give us a good idea of how multiple forces add. If two people push in different directions on a third person, as illustrated in Figure 7.1, we might expect the total force to be in the direction shown. Since force is a vector, it adds just like other vectors, as illustrated in Figure 7.1 for two ice skaters. Forces, like other vectors, are represented by arrows and can be added using the familiar tail-to-tip method or by trigonometric methods.
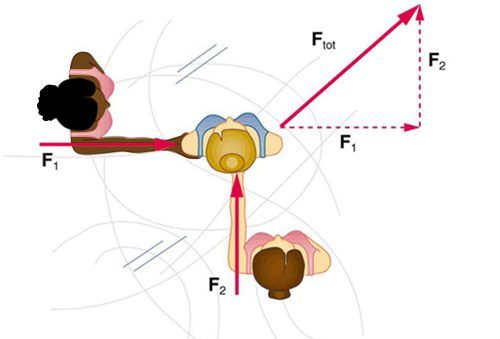
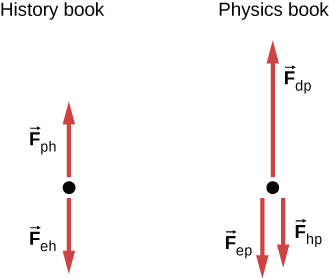
To illustrate all external forces on a body we draw a free-body diagram. The body is represented by a single isolated point (or free body), and only those forces acting on the body from the outside (external forces) are shown. (These forces are the only ones shown because only external forces acting on the body affect its motion. We can ignore any internal forces within the body.) Free-body diagrams are very useful in analyzing forces acting on a system and are employed extensively in the study and application of Newton’s laws of motion.
The standard unit of force is Newton (N). Referring to Newton’s Second Law of motion we see that
1 N=1 kgm/s2
In other words, it takes 1N of unbalanced force to make a 1kg mass accelerate at a rate of 1m/s2. In the United States, a more customary unit for force is the pound (lb). 1N=0.225lb.
Mass and Inertia
As mentioned earlier, inertia is the resistance of an object against change in its motion. Inertia is the inherent tendency of an object to maintain its state of motion. There are many everyday situations where we encounter inertia. Let’s take a look at a few.
Imagine you are riding in a car and the car suddenly stops. You feel like being thrown forward. Your body that was initially moving with the car has a tendency to maintain that motion (this is inertia). When the car suddenly stops, your body, maintaining its motion, is still moving forward. That’s why you feel like you have been thrown forward when the car slows down.
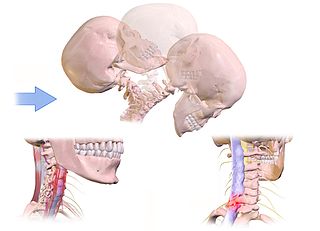
The situation described above can result in a whiplash injury which is another illustration of inertia. If you are wearing a seat belt then as the car suddenly slows down your body is kept in place with the seat belt, but your head is still moving forward (this is inertia). This may cause injury to the neck and result in whiplash which is characterized by damage done to the intervertebral joints, discs, and ligaments, cervical muscles, and nerve roots.
Have you noticed how much easier it is to tear off a piece of toilet paper when the roll is full? The tendency of the full roll to stay motionless is inertia. Less toilet paper on the roll results in less mass and therefore less inertia.
The following video demonstrates more examples. Try to explain how each event can be explained using the concept of inertia?
Example 6.1
Suppose that the net external force (push minus friction) exerted on a lawnmower is 51 N (about 11 lb.) parallel to the ground. The mass of the mower is 24 kg. What is its acceleration?
Solution
This problem involves only motion in the horizontal direction. We are given the net force. We can use Newton’s Second Law to solve for the acceleration.
![]()
![]()
![]()
Discussion
The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. This is a result of the vector relationship expressed in Newton’s Second Law. There is no information given in this example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the force exerted by the person pushing the mower must be greater than the friction opposing the motion (since we know the mower moved forward), and the vertical forces must cancel because no acceleration occurs in the vertical direction (the mower is moving only horizontally). The acceleration found is small enough to be reasonable for a person pushing a mower.
Example 6.2
Before space flights carrying astronauts, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets.
Calculate the magnitude of the force exerted by each rocket, called its thrust T, for a four-rocket propulsion system. The sled’s initial acceleration is 49m/s2, the mass of the system is 2100kg, and the force of friction opposing the motion is 650N.
Solution
Although forces are acting both vertically and horizontally, we assume the vertical forces cancel because there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Now let’s apply Newton’s Second Law.
![]()
![]()
![]()
Discussion
The numbers are quite large, so the result might surprise you. Experiments such as this were performed in the early 1960s to test the limits of human endurance, and the setup was designed to protect human subjects in jet fighter emergency ejections. Speeds of 1000 km/h were obtained, with accelerations of 45 g’s. (Recall that g, acceleration due to gravity, is 9.8m/s2. When we say that acceleration is 45 g’s, it is 45×9.8m/s2 which is approximately 440m/s2. Although living subjects are not used anymore, land speeds of 10,000 km/h have been obtained with a rocket sled.
Force as an interaction between two objects
Force is the result of interaction between two objects. Therefore, the first step in identifying a force is to identify the two objects that are interacting. A few examples are given below.
Video Example – Force between two vehicles colliding and their acceleration
Video Example – Force between two blocks accelerating together
Attributions
This chapter contains material taken from Openstax University Physics Volume 1 and is used under a CC BY 4.0 license. Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction
To see what was changed, refer to the List of Changes.
questions and problems
Questions
- Newton’s Third Law is sometimes stated as “for every action, there is a reaction.” Explain the meaning of “action” and “reaction” in this statement.
- If action and reaction forces are always equal and in opposite directions, how is it ever possible to have an unbalanced force on an object?
- What is the meaning of “net force”? Give a few examples where there is a “net force” on an object and explain what the net force is in each case.
- Is it possible for two objects to apply forces on each other without touching each other? Explain.
Problems
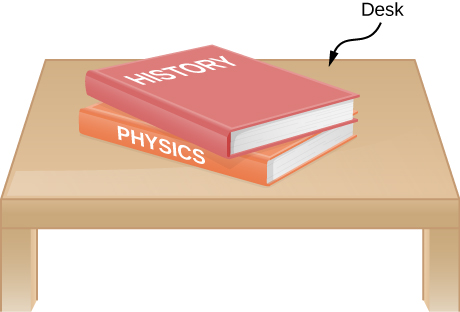
- Draw the necessary diagrams to show all action-reaction forces that represent the interaction between each block in figures a, b, c, and the book in figure d and everything else. Ignore friction between all surfaces. For each force, in parenthesis indicate what object is applying it. Mark all action-reaction pairs with the same symbol, and label them the same.
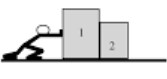
(a) 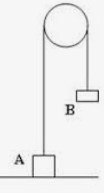
(b) 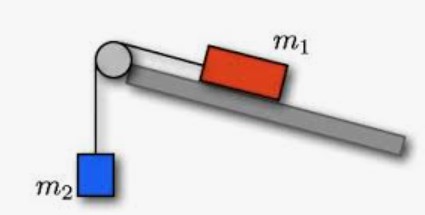
(c) 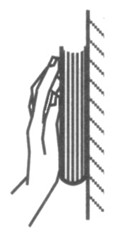
(d) - The figure below shows a tug-of-war between two people. Draw the necessary diagrams to show all action-reaction forces that represent the interaction between the person on the left and everything else. Do not ignore friction between the feet and the ground. For each force, in parenthesis indicate what object is applying it. Mark all action-reaction pairs with the same symbol, and label them the same.

- The figure shows a person pulling a tire with a rope. Identify all the action-reaction force pairs. Do not ignore friction. For each force, in parenthesis indicate what object is applying it. Mark all action-reaction pairs with the same symbol, and label them the same. The mass of the rope is negligible.