Momentum
Unit 12 – Collisions, Explosions, and Center of Mass
Last Update: 6/28/2024
collisions and explosions
As we learned in our discussion of energy, if the forces acting on a system are conservative, the mechanical energy of the system is conserved. We can extend this idea to colliding objects. If the force between two objects in a collision is conservative, the mechanical energy of the system is conserved in that collision. This type of collision is called elastic collision. For example, the force between two gas molecules is the electromagnetic force, which is a conservative force. So, the collision of two gas molecules is elastic.
Therefore, in an elastic collision, like any other collision, we can apply the conservation of momentum. On top of that, we can also apply conservation of kinetic energy.
Elastic Collision:
![]()
and
![]()
In most cases, when two objects collide some of the initial kinetic energy of the system is converted to other types of energy such as sound or thermal energy, or kinetic energy leaves the system in the form of work done on the colliding objects. This work leads to the deformation of the objects. For example, when two cars collide, they get dented and damaged. These deformations take energy and the energy comes from the initial kinetic energy of the colliding cars. Therefore, most collisions are not elastic. We call this type of collision, an inelastic collision. In analyzing an inelastic collision we can only apply the conservation of momentum.
Inelastic Collision:
![]()
![]()
Sometimes though, the amount of kinetic energy lost in a collision is so small that for all practical purposes, we can treat the collision as being elastic. For example, the collision of billiard balls on a pool table is very nearly elastic.
Problem Solving Strategy-Collisions
In a closed system, there is no interaction between the objects and anything external and the external force on the system is zero. Therefore, a closed system always conserves momentum. A closed system might also conserve kinetic energy, but very often it doesn’t. Energy-momentum problems confined to a plane (as ours are) usually have two unknowns. Generally, this approach works well:
- Define a closed system.
- Write down the expression for conservation of momentum in component form, in x and y directions.
- If kinetic energy is conserved, write down the expression for conservation of kinetic energy.
- You now have a system of equations (usually two equations in two unknowns) which you solve by standard methods.
Example 12.1 – Colliding Hockey Pucks
Two ice hockey pucks of different masses are on a flat, horizontal hockey rink. The red puck has a mass of 150 grams, and is motionless; the blue puck has a mass of 120 grams and is moving at 2.5 m/s to the left. It collides with the motionless red puck (Figure 12.1). If the collision is head-on and perfectly elastic, what are the final velocities of the two pucks?
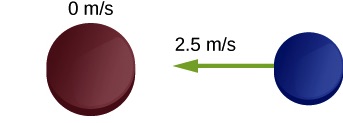
Solution
Since the collision is head-on, it means that the pucks collide center-to-center and all the velocities are along a straight line. Therefore this is a one-dimensional collision. We take the positive direction to be to the right and use positive and negative signs to indicate the direction of the velocities and momenta.
We take the system to consist of the two pucks. Since the collision is elastic, we can apply the conservation of kinetic energy in addition to the conservation of momentum to this system.
Let’s start with the conservation of momentum equation.
![]()
![]() Equation 1
Equation 1
We have two unknowns in this equation. We need one more equation to solve for these unknowns. The second equation is obtained by applying the conservation of kinetic energy.
![]()
![]() Equation 2
Equation 2
We can use the method of substitution to solve for the final velocities. Let’s use Equation 1 and solve for v1f in terms of v2f, and then replace v1f in Equation 2.
Equation 1 → ![]()
![]()
Now, let’s rewrite Equation 2 and replace v1f with what we found above.
Equation 2 → ![]()
- Cancel
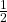 on both sides.
on both sides. - Use
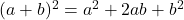 to expand
to expand 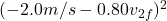
![]()
![]()
![]()
![]()
![]() or
or ![]()
Notice that the initial velocity of puck 2 was -2.5m/s. So a final velocity of -2.5m/s suggests that nothing has happened! In other words, momentum and kinetic energy are of course conserved if the two pucks never collide to begin with. So, -2.5m/s is the trivial answer and not the one we are looking for. When the two pucks collide, the final velocity of puck 2 is ![]()
Now we can find the final velocity of puck 1.
![]()
![]()
![]()
So, after the collision, the blue puck turns around and moves to the right with a velocity of 0.28m/s, while the red one moves to the left with a velocity of -2.2m/s.
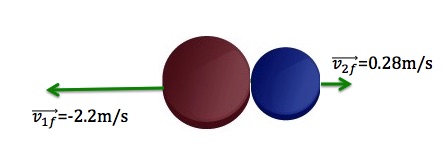
Video Example – one dimensional collision of two toy cars
Example 12.2 – Colliding Carts
Let’s re-examine Example 11.6
Two carts in a physics lab roll on a level track, with negligible friction. These carts have small magnets at their ends so that when they collide, they stick together (Figure 12.12). The first cart has a mass of 675 grams and is rolling at 0.750 m/s to the right; the second has a mass of 500 grams and is rolling at 1.33 m/s, also to the right. After the collision, what is the velocity of the two joined carts?

We found the final velocity to be ![]()
This type of collision, where the two objects stick together after the collision is called a perfectly inelastic collision. Let’s determine the percentage of kinetic energy that is dissipated in this collision.
Solution
The system consists of two carts. The initial kinetic energy of the system is
![]()
![]()
Now, let’s find the final kinetic energy of the system.
![]()
![]()
The percentage of kinetic energy lost in this collision is
% energy lost![]()
% energy lost=-7.6%
Video Example – Pendulum ball hitting a stationary block
Video Example – Inelastic collision of a car and a truck
Example12.3
Ball 1 moving along the y-axis with a speed of 15.0m/s strikes ball 2 which is initially at rest. Ball 1 and ball 2 have the same mass. After the collision, ball 1 has deviated by an angle of 50° from its original direction, and ball 2 moves off at 30° from the original direction, as shown below.
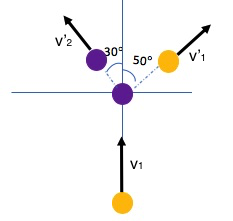
a) Find the speed of the two balls after the collision.
b) Is this collision elastic?
Solution for (a)
The system of interest consists of two balls. Like in any other collision, the momentum of the system is conserved. Let’s apply the conservation of momentum in component form. Since the two balls have the same mass, let’s use m for both masses.
|
|
Now, let’s combine the results and eliminate one unknown between the two equations.
![]()
![]()
And
![]()
![]()
Solution for (b)
To see if the kinetic energy of the system is conserved, we need to compare the initial kinetic energy of the system with its final kinetic energy.
![]()
![]()
![]()
![]()
Since ![]() the kinetic energy is not conserved in this collision. The kinetic energy of a system can decrease noticeably after a collision if, for example, one of the objects becomes damaged and dented. In that case, some of the kinetic energy does work to deform the ball.
the kinetic energy is not conserved in this collision. The kinetic energy of a system can decrease noticeably after a collision if, for example, one of the objects becomes damaged and dented. In that case, some of the kinetic energy does work to deform the ball.
Explosions
The first possibility is that a single object may break apart into two or more pieces. An example of this is a firecracker, a bow and arrow, or a rocket rising through the air toward space. These can be difficult to analyze if the number of fragments after the collision is more than about three or four; nevertheless, the total momentum of the system before and after the explosion is identical.
Note that if the object is initially motionless, then the system (which is just the object) has no momentum and no kinetic energy. After the explosion, the net momentum of all the pieces of the object must sum to zero (since the momentum of this closed system cannot change). However, the system will have a great deal of kinetic energy after the explosion, although it had none before. Thus, we see that, although the momentum of the system is conserved in an explosion, the kinetic energy of the system most definitely is not; it increases. This interaction—one object becoming many, with an increase in the kinetic energy of the system—is called an explosion.
![]()
![]()
Where does the energy come from? Does conservation of energy still hold? Yes; some form of potential energy is converted to kinetic energy. In the case of gunpowder burning and pushing out a bullet, chemical potential energy is converted to the kinetic energy of the bullet, and of the recoiling gun. For a bow and arrow, it is elastic potential energy in the bowstring.
Example 12.4 – Exploding Scuba Dive Tank
A common scuba tank is an aluminum cylinder that weighs 14.4kg empty. When full of compressed air, the internal pressure is between 2500 and 3000 psi (pounds per square inch). Suppose such a tank, which had been sitting motionless, suddenly explodes into three pieces. The first piece, weighing 4.5kg, shoots off horizontally at 105m/s; the second piece with a mass of 3.2kg shoots off at 97m/s, also in the horizontal plane, but at a 19º angle to the first piece.
a) What are the mass and initial velocity of the third piece?
b) Determine the initial and final kinetic energy of the system.
Solution for (a)
Explosion is another situation where momentum is conserved because if there is any external force acting on the exploding object, that external force is almost always negligible compared to the internal forces that cause the explosion. In this problem, the system is the tank. Since the tank was initially at rest, the initial momentum of the system was zero. Conservation of momentum requires that the final momentum, which is the sum of the momenta of the individual pieces after the explosion, be zero as well. Therefore we expect the pieces to fly off as shown below.
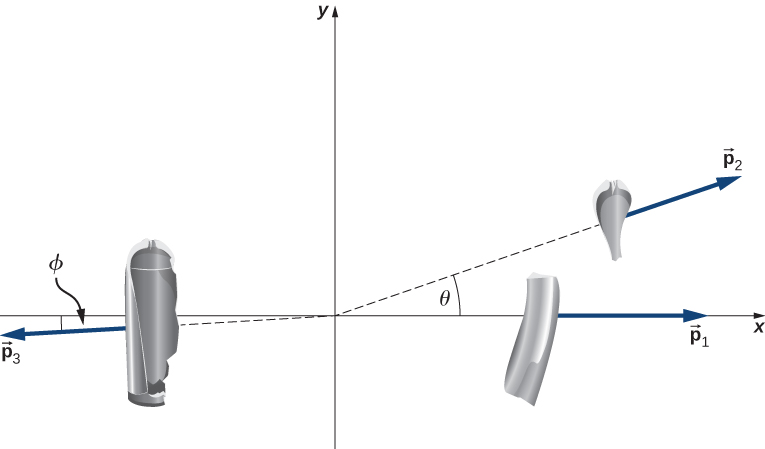
Applying conservation of momentum to this system we get
![]()
![]()
Now we need to break up these vectors into components and write the equation for the conservation of momentum in component form in both x and y directions.
m3=14.4kg -(4.5kg+3.2kg)
m3=6.7kg
Now we can use the components to determine the magnitude and direction of the velocity of the third piece.
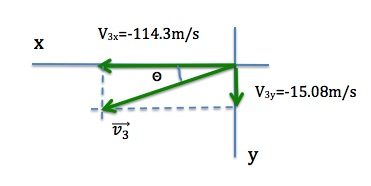 |
|
We need to express the angle relative to the positive x-axis.
7.5º+180º=187.5º
The velocity of the third piece is ![]()
Solution for (b)
Since the tank was initially at rest, ![]()
After the explosion, the kinetic energy of the system is:
![]()
![]()
In UNIT 11, we saw how airbags reduce the force of impact by increasing the duration of the force. Another safety feature of modern vehicles that demonstrates the same concept is the “crumple zone”. Cars are deliberately designed to deform and crumple in a crash to improve the safety of the occupants. The function of the crumple zone is twofold. One is to increase the duration of impact. This results in the reduction of the force. The second function is to absorb at least a portion of the kinetic energy of the colliding vehicles to maximize the safety of the occupants.
center of mass
The center of mass is the weighted average position of all the pieces that make up an object, with each position weighted according to the mass of that piece. The center of mass is a useful concept because the center of mass of an object behaves like a point mass. Consider the tennis racket shown in the video. The overall motion of the racket is very complicated, but its center of mass follows a parabolic path just like any other point mass following a projectile motion.
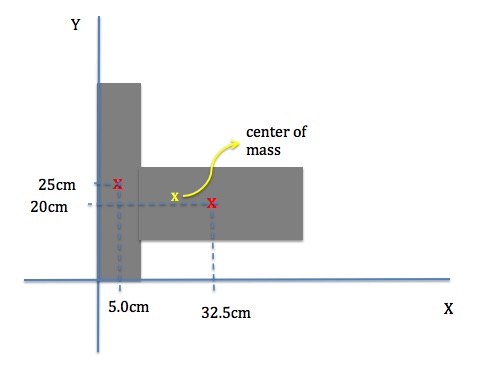
Another way the concept of the center of mass is useful is that it greatly simplifies analyzing the motion of a system that consists of many parts. Consider a system that is made up of three parts as shown in Figure 12.4. the yellow x marks the position of the center of mass of objects 1, 2, and 3.

Applying Newton’s Second Law in the form of an impulse-momentum equation to this system yields
![]()
But notice that any interaction (meaning collision and force) among the three objects does not change the momentum of the system. As we have seen, this is the principle of conservation of momentum. The only way to change the momentum of the system as a whole is to have an interaction between the system and something on the outside of it. In other words, an external force is necessary to change the momentum of the system. We should then replace ![]() in the above equation with
in the above equation with ![]() to make the point clear.
to make the point clear.
![]()
What’s that got to do with the center of mass? Well, The motion of the system as a whole can be represented by the motion of its center of mass. Just like the complicated motion of the tennis racket in the video could be represented with the simple motion of its center of mass. And the center of mass behaves like a point particle. No matter how complicated the motion of the individual parts in the system gets, the center of mass of the system is not affected by these internal interactions. The only thing that can change the motion of the center of mass is an external force.
The following PhET simulation helps visualize this idea. Click on the picture to activate the simulation. Select “Explore 2D” and check the center of mass option. The X on the screen shows the position of the center of mass of the two balls. You can set the initial velocities and masses to whatever you wish and run the simulation. Notice that when the balls collide with each other the motion of the center of mass does not change, but when one of the balls collides with the wall of the container and the system experiences an external force the motion of the center of mass changes.
You can also use the PhET simulation above to verify the results of some of the numerical examples in this unit and the answers to some of your homework assignments.
Finding the position of the center of mass
The center of mass of a uniform object is at its geometric center. For example, the center of mass of a uniform piece of plywood cut in the shape of a square is in the center of the square, or the center of mass of a donut is in the center of the donut. Notice that the center of mass is not necessarily where there is material substance (like the donut).
If an object is not uniform or has an irregular shape, we can determine its center of mass by hanging it from two different points. Suppose we want to find the center of mass of a piece of wood cut in this shape.

We can hang this from two different points and let it come to equilibrium. Then we draw a line from the pivot point straight down. The point of intersection of these two lines is the center of mass of the object (red x).

We can also calculate the position of the center of mass of a system made up of several point objects. To do this, we pick a coordinate system and calculate the x and y coordinates of the center of mass (xcm, ycm) as follows.
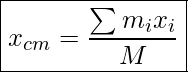 X-Coordinate Of Center Of Mass
X-Coordinate Of Center Of Mass
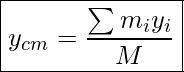 Y-Coordinate Of Center Of Mass
Y-Coordinate Of Center Of Mass
Where mi is the mass of a small piece, xi is the x-coordinate of mi, yi is the y-coordinate of mi, and M is the total mass of the system.
As an example, suppose we want to determine the center of mass of a system made up of three spherical objects with masses m1, m2, and m3.

![]()
![]()
Example12.5 – Center of Mass Of A Piece Of Cardboard
Calculate the position of the center of mass of a uniform piece of cardboard cut in the following shape.

Solution
We pick a coordinate system with the axes along the edge of the cardboard shape to simplify calculations. We break up this shape into two rectangles and mark the center of mass of the rectangles in the coordinate system.

We don’t know the mass but since the cardboard is uniform it has the same density throughout. We define a two-dimensional density, d, as mass/area, and express mass in terms of area.
![]()
![]()
![]()
Now we can calculate the x and y coordinates of the center of mass.
![]()
![]()
![]()
Repeat the same process to find the y-coordinate.
![]()
![]()
![]()
Stability and Center of mass
A system is said to be in stable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction opposite to the direction of the displacement. For example, a marble at the bottom of a bowl will experience a restoring force when displaced from its equilibrium position. This force moves it back toward the equilibrium position. A system is in unstable equilibrium if, when displaced, it experiences a net force or torque in the same direction as the displacement from equilibrium. A system in unstable equilibrium accelerates away from its equilibrium position if displaced even slightly. An obvious example is a ball resting on top of a hill. Once displaced, it accelerates away from the crest. A system is in neutral equilibrium if its equilibrium is independent of displacements from its original position. A marble on a flat horizontal surface is an example.
When we consider how far a system in stable equilibrium can be displaced before it becomes unstable, we find that some systems in stable equilibrium are more stable than others. In general, a high center of mass or a small support base makes a structure less stable.
Human Stability
The center of mass of a person’s body is above the pivots in the hips, which is relatively high compared to the size of the support base formed by the feet, so displacements must be quickly controlled. This control is a function that is developed when we learn to hold our bodies erect as infants. For increased stability, while standing, the feet should be spread apart, giving a larger base of support. Stability is also increased by bending the knees, which lowers the center of gravity toward the base of support. A cane, a crutch, or a walker increases the stability of the user by widening the base of support. Due to their disproportionately large heads, young children have their center of gravity between the shoulders, rather than down near the hips, which decreases their stability and increases the likelihood of reaching a tipping point.
Walking is an act of moving in and out of equilibrium. To walk we:
- Push against the ground with one foot using normal force and friction while leaning forward, lifting the other foot, and moving it forward. This moves the center of mass outside the support base formed by the (now) back foot. Having passed the tipping point, the body would fall except:
- The front foot lands, slowing the forward motion of your center of gravity and creating a new support base so that you are no longer past the tipping point. The front foot becomes the back foot and begins to push off.
- Repeat.
Slipping happens when the coefficient of friction between feet and the walking surface is too small and the frictional force is not large enough to prevent your feet from sliding as the back foot pushes off and/or the front foot tries to slow the forward motion of your center of gravity.
Tripping happens when your foot does not move forward quickly enough to shift your support base below your center of gravity and you either fall over or have to rapidly move your feet into position just in time (stumble).
Attributions
This chapter contains material taken from
Openstax College Physics-Linear Momentum and Collisions, and Openstax University Physics Volume 1 – Linear Momentum and Collisions, and is used under a CC BY 4.0 license. Download these books for free at Openstax
To see what was changed, refer to the List of Changes
The section on Stability and Center of Mass is taken from
College Physics-Openstaxcollege
Body Physics: Motion to Metabolism by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
questions and problems
questions
- [openstax college phys. quest. 8.13] Can objects in a system have momentum while the momentum of the system is zero? Explain.
- What is an elastic collision?
- [openstax univ phys. vol. 1 quest 9.7] Under what circumstances is momentum conserved?
problems
- [openstax univ. phys. vol. 1 – 9.43]A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg bowling pin, which is scattered at an angle of 15.8° to the initial direction of the bowling ball and with a speed of 15.0 m/s.
- Calculate the final velocity (magnitude and direction) of the bowling ball.
- Is the collision elastic?
- [openstax univ. phys. vol. 1 – 9.46] A 100-g firecracker is launched vertically into the air and explodes into two pieces at the peak of its trajectory. If a 72.0-g piece is projected horizontally to the left at 20.0 m/s, what is the speed and direction of the other piece?
- [openstax univ. phys. vol. 1 – 9.45] A 90.0-kg ice hockey player hits a 0.150-kg puck, giving the puck a velocity of 45.0 m/s. If both are initially at rest and if the ice is frictionless, how far does the player recoil in the time it takes the puck to reach the goal 15.0 m away?
- [openstax univ. phys. vol. 1 – 9.47] In an elastic collision, a 400-kg bumper car collides directly from behind with a second, identical bumper car that is traveling in the same direction. The initial speed of the leading bumper car is 5.60 m/s and that of the trailing car is 6.00 m/s. What are their final speeds?
- [openstax univ. phys. vol. 1 – 9.50] You are standing on a very slippery icy surface and throw a 1.00-kg football horizontally at a speed of 6.70 m/s. What is your velocity when you release the football? Assume your mass is 65.0 kg.
- [openstax univ. phys. vol. 1 – 9.51] A child rides a sled down a hill and then coasts along the flat section at the bottom. The mass of the child and the sled is 35.0kg. Along the flat section at the bottom, a second child with a mass of 35.0kg jumps on the sled as it passes by her. If the speed of the sled is 3.50 m/s before the second child jumps on, what is its speed after she jumps on?
- [openstax univ. phys. vol. 1 – 9.54 part b added)] A billiard ball, labeled 1, moving horizontally strikes another billiard ball, labeled 2, at rest. Before impact, ball 1 was moving at a speed of 3.00 m/s, and after impact, it is moving at 0.500m/s at 50.0° from the original direction.
- If the two balls have equal masses of 300 g, what is the velocity of the ball 2 after the impact?
- Was this collision elastic? Justify your answer.
- Assuming the collision lasts for 0.0500s, find the magnitude and direction of the force on ball 1.
- [openstax univ. phys. vol. 1 – 9.61] An oxygen atom (mass 16 u) moving at 733 m/s at 15.0° with respect to the positive x-direction collides and sticks to an oxygen molecule (mass 32 u) moving at 528 m/s at 128° with respect to the positive x-direction. The two stick together to form ozone. What is the final velocity of the ozone molecule?
- [openstax univ. phys. vol. 1 – 9.62] Two cars of the same mass approach an extremely icy four-way perpendicular intersection. Car A travels northward at 30 m/s and car B is traveling eastward. They collide and stick together, traveling at 28° north of east. What was the initial velocity of car B?
- [openstax univ. phys. vol. 1 – 9.63] Three point-masses are placed at the corners of a triangle as shown in the figure below. Find the location of the center of mass of the system. Use three significant digits for all the given values.
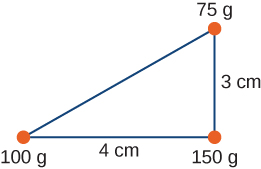
fig-prob12.10 [Image Description] - A block with a mass of 1.50kg is sliding on a frictionless horizontal surface at a speed of 10.0m/s when it strikes another block of mass 0.500kg that is at rest at the base of an incline. The two blocks stick together and slide up the frictionless 35.0° incline.
- Find the distance the blocks travel along the incline before they momentarily stop.
- What percentage of the kinetic energy is lost in the collision between the blocks?
- [openstax univ. phys. vol. 1 – 9.55] A projectile of mass 2.00kg is fired in the air with a velocity of 50.0m/s @40.0°. At the highest point in its flight, the projectile breaks into three parts of mass 1.00kg, 0.700kg, and 0.300kg. the 1.00kg part falls straight down after breakup with an initial speed of 10.0m/s, the 0.700kg part moves in the original direction of the projectile at the instant it explodes, and the 0.300kg part goes straight up.
- Find the speeds of the 0.300kg and 0.700kg pieces immediately after the breakup.
- What is the maximum height reached by the 0.300kg piece relative to the ground?
- Where does the 0.700kg piece land relative to where the projectile was initially fired from?
- Two balls hang side-by-side from strings with a length of 0.500m. Ball A is 600g, and ball B is 300g. Ball A is pulled to the side by an angle of 25.0° and released from rest.
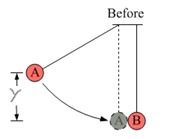
- Determine the speed of ball A before its collision with ball B.
- Determine the velocity of the two balls right after the collision, assuming the collision is perfectly elastic.
- To what maximum angle does ball B swing after the perfectly elastic collision?
- Determine the velocity of the two balls right after the collision, assuming they stick together.
- If they stick together, to what maximum angle do the balls swing after the collision?
- Blocks A with a mass of 0.750kg and block B with a mass of 0.200kg are pressed together with a spring between them. They initially rest on a frictionless horizontal surface of a table. When the blocks are released from rest, the spring pushes them apart. Block B moves to the right at vfB=3.00m/s and eventually falls off the table and lands on the ground, 1.50m below. Block A moves to the left and eventually moves up a 30.0° ramp. The coefficient of kinetic friction between block A and the ramp is 0.150.
- Find the distance, d, that block A slides up the ramp.
- Find the distance, x, between the edge of the table and where block B lands on the ground.
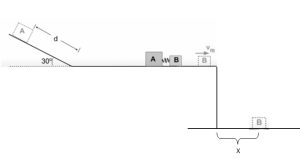
fig-prob12.14 [Image Description]
image descriptions
fig-prob12.10 image description – A right triangle is shown. A 3cm vertical line and a 4cm horizontal line form the right angle. At the corner where the two lines meet there is a 150g point mass. At the top of the 3cm vertical line, there is a 75g point mass. At the other end of the horizontal line, there is a 100g point mass. [Return to the image]
fig-prob12.14 image description -Blocks A and B are pressed together with a spring and rest on a horizontal surface. Block A is on the left and faces a 30-degree incline. A faint drawing of block B shows it moving to the right after being released, and then falling off the edge of the table and landing on the ground. The horizontal distance between the edge of the table and where block B lands is marked as x. A faint drawing of block A shows it coming to rest on the incline. the distance traveled by block A up the incline is marked as d. [Return to the image]


