Unit 12 – Linear Momentum, Impulse, and Momentum Conservation

Beta Keramati

Momentum

Last Update: 12/5/2022

Linear Momentum and Newton’s Second Law

Momentum is a quantity that represents the amount of motion in an object. Linear momentum is defined as the product of mass and velocity.

$\boxed{\vec P = m \vec v}$ Linear Momentum

Since velocity is a vector, momentum is also a vector. In SI units, momentum is measured in kgm/s.

Example 12.1 – A Football Player And A Football

Calculate the magnitude of the momentum of a 110-kg football player running at 8.00 m/s, and compare it with the magnitude of the momentum of a hard-thrown 0.410-kg football that has a speed of 25.0 m/s.

Solution

No information is given regarding direction, and so we can calculate only the magnitude of the momentum by using $\vec P = m \vec v$

Momentum of the player:

$P_{player} =(110kg)(8.00m/s)$

$P_{player} =880kgm/s$

Momentum of the ball:

$P_{ball} =(0.410kg)(25.0m/s)$

$P_{ball} =10.3kgm/s$

Discussion

The ratio of the player’s momentum to that of the ball is

$\frac{P_{player}}{P_{ball}} = \frac{880kgm/s}{10.3kgm/s}$

$\frac{P_{player}}{P_{ball}} = 85.9$

Although the ball has greater velocity, the player has a much greater mass. Thus the momentum of the player is much greater than the momentum of the football, as you might guess. As a result, the player’s motion is only slightly affected if he catches the ball. We shall quantify what happens in such collisions in terms of momentum in later sections.

Newton’s Second Law of motion, $\vec a = \frac{\sum \vec F}{m}$ , can be expressed in terms of momentum as shown below. As we will see shortly, this alternative expression of Newton’s Second Law is more convenient to use in many situations.

$\vec a = \frac{\sum \vec F}{m}$

$\frac{\vec v - \vec v_0}{\Delta t} = \frac{\sum \vec F}{m}$

$m(\vec v - \vec v_0)=(\sum \vec F)(\Delta t )$

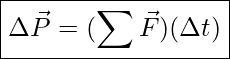$\boxed{\Delta \vec P=(\sum \vec F)(\Delta t )}$ Impulse-Momentum Equation

Therefore, there are two ways to express Newton’s Second Law.

$\vec a = \frac{\sum \vec F}{m}$ is the same as $\Delta \vec P=(\sum \vec F)(\Delta t )$

The quantity, $(\sum \vec F)(\Delta t )$ , is called the net impulse, and the equation, $\Delta \vec P=(\sum \vec F)(\Delta t )$ , is also known as the impulse-momentum equation. In SI system, we usually use the units of Ns for impulse, and kgm/s for momentum, but of course, Ns=kgm/s. Notice that impulse is also a vector quantity. The impulse delivered by a force is in the same direction as that force.

Example 12.2 – Venus Williams’ Racquet

During the 2007 French Open, Venus Williams hit the fastest recorded serve in a premier women’s match, reaching a speed of 58 m/s (130 mph). What is the average force exerted on the 0.057-kg tennis ball by Venus Williams’ racquet, assuming that the initial horizontal component of the ball’s velocity before impact is negligible and that the ball remained in contact with the racquet for 5.0 ms (milliseconds)?

Solution

There are two ways to solve this problem:

Using kinematics equations along with Newton’s Second law in the form of $\vec a = \frac{\sum \vec F}{m}$
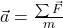
Using impulse-momentum equation, which is Newton’s Second Law in the form of $\Delta \vec P=(\sum \vec F)(\Delta t )$

Solution using the first method

The horizontal velocity of the ball changes from 0 to 58m/s in 5.0ms. From this, we can obtain the acceleration.

$v=at + v_0$

$58m/s=a(5.0 \times 10^{-3} s) + 0$

$a=11600m/s^2$

At the instant the ball is hit, the forces acting on the ball are the gravitational force applied by Earth and the force of the racquet. But since the force of the racquet is significantly larger than the gravitational force, we can ignore the gravitational force. Now we apply Newton’s Second Law.

$\vec a = \frac{\sum \vec F}{m}$

$11600m/s^2 = \frac{F_{racquet}}{0.057kg}$

$F_{racquet}=660N$

Solution using the second method

This problem involves only one dimension because the ball starts from having no horizontal velocity component before impact. The impulse-momentum equation which is the same thing as Newton’s second law stated in terms of momentum is

$\Delta \vec P=(\sum \vec F)(\Delta t )$

Since momentum is $\vec P = m \vec v$ we can re-write the equation above as

$(0.057kg)(58m/s)-(0.057kg)(0m/s)=(\sum F)(5.0 \times 10^{-3} s)$

Therefore

$\sum F=660N$

At the instant the ball is hit, the forces acting on the ball are the gravitational force applied by Earth and the force of the racquet. But since the force of the racquet is significantly larger than the gravitational force, we can ignore the gravitational force and conclude that

$F_{racquet}=660N$

Discussion

This quantity was the average force exerted by Venus Williams’ racquet on the tennis ball during its brief impact. Notice that the gravitational force on the tennis ball is F_g=(0.057kg)(9.8m/s²)=0.56N. This force is significantly smaller than the 660N average force applied by the racquet and that’s why we could ignore it in this problem.

Example12.3 – The Physics Of Airbags

A car traveling at 27 m/s collides with a building. The collision with the building causes the car to come to a stop in approximately 1 second. The driver, who has a mass of 87.8 kg, is protected by a combination of a variable-tension seatbelt and an airbag. (In effect, the driver collides with the seatbelt and airbag and not with the building.) The airbag and seatbelt slow his velocity, such that he comes to a stop in approximately 2.5 s.

What average force does the driver experience during the collision?
Without the seatbelt and airbag, his collision time (with the steering wheel) would have been approximately 0.20 s. What force would he experience in this case?

Solution for (a)

We can use the impulse-momentum equation to determine the average force. Let’s take the positive direction to be to the right in reference to figure 12.1.

$\Delta \vec P=(\sum \vec F)(\Delta t )$

$0-(87.8kg)(2.7m/s)=(\sum \vec F)(2.5s)$

$\sum \vec F=-948N$

Solution for (b)

Using the same approach as part (a) we get

$\Delta \vec P=(\sum \vec F)(\Delta t )$

$0-(87.8kg)(2.7m/s)=(\sum \vec F)(0.20s)$

$\sum \vec F=-11900N$

Discussion

In both cases the force is negative. This indicates a force to the left as demonstrated in Figure 12.1. As you can see in this example the value of a seatbelt and airbag is how greatly it reduces the force on the vehicle occupants. For this reason, airbags have been required on all passenger vehicles in the United States since 1991, and have been commonplace throughout Europe and Asia since the mid-1990s. The change of momentum in a crash is the same, with or without an airbag; the force, however, is vastly different.

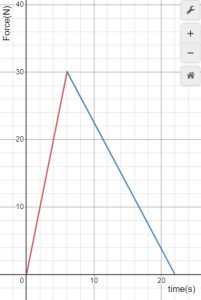
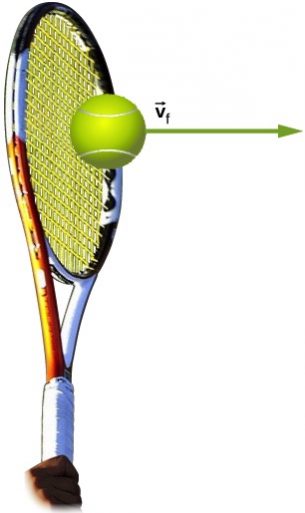
It is easy to see that the impulse delivered by a constant force is equal to the area under the plot of Force vs time.

This idea can be generalized to any force. It can be shown mathematically that the area under any force vs time curve, is in fact equal to the impulse delivered by that force. Consider hitting a tennis ball with a racquet. The force on the tennis ball is not constant and the plot of force vs time looks like the graph in Figure 12.4. The area under the curve represents the impulse delivered by the racquet on the ball.

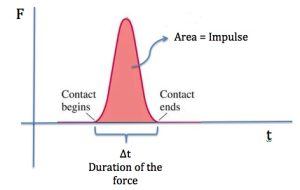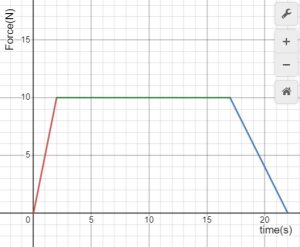
When the force is not constant, we can still use the impulse-momentum equation to determine the average force. The average force is the constant force that delivers the same impulse to the object in the same time interval, as shown in figure 12.5.

Example 12.4

Notice that the forces we calculated in Examples 12.2 and 12.3 are average forces.

In example 12.3, the driver goes through the same change in momentum whether he collides with the airbag or the steering wheel. Therefore he receives the same impulse in both situations. But when he hits the airbag the impulse is delivered by a small force that acts over a long time, whereas collision with the steering wheel results in a large force that acts for a short time. This is demonstrated in Figure 12.6

Video Example – Impulse from the graph of force vs time

Video Example – Impulse on a hockey puck perpendicular to the direction of motion

Newton’s Third law and conservation of momentum

As we saw earlier when two objects interact they apply forces on each other. As expressed in Newton’s Third Law, these forces are equal in magnitude and act in opposite directions. In this section, we examine the interaction between two objects in terms of momentum and impulse.

Suppose two boxes with masses m₁and m₂ sliding on a frictionless surface collide with one another as depicted below.

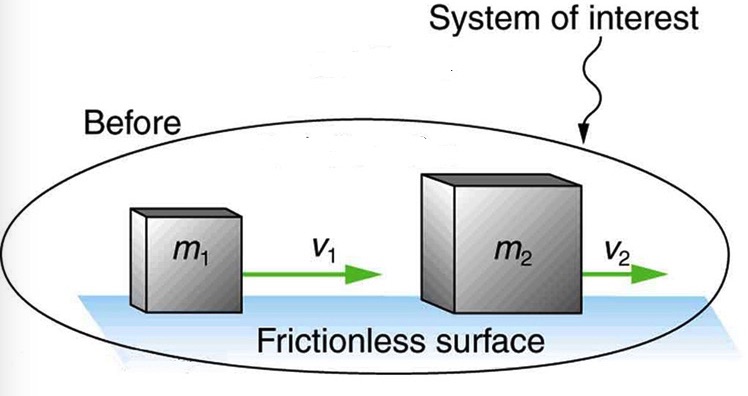
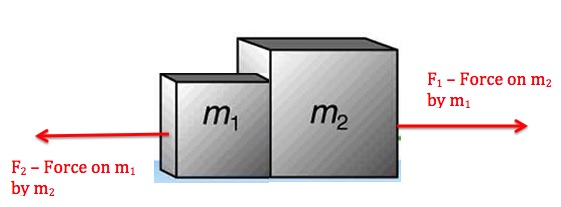
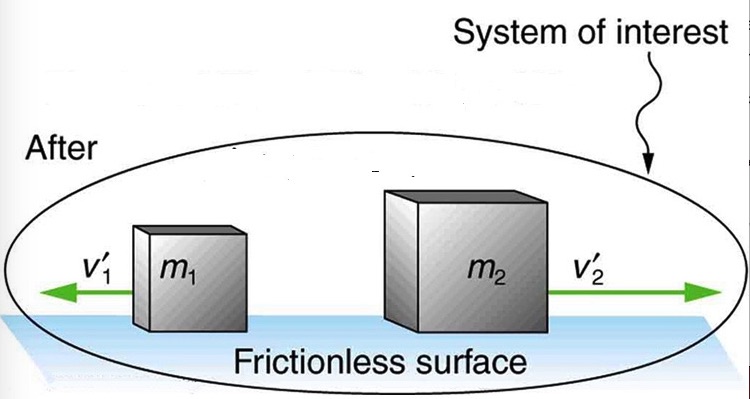
During the collision, the boxes apply equal size forces on each other. This means F₁=-F₂. Also, the duration of these forces is equal. In other words, as long as m₁is pushing m₂ to the right, m₂ is pushing m₁ to the left. If we represent the duration of these forces with Δt, then we get

$\vec F_1\Delta t =- \vec F_2 \Delta t$

$\vec F\Delta t$ is impulse and impulse is equal to change in momentum.

$\Delta \vec P=(\sum \vec F)(\Delta t )$

Since the only force on m₁ is F₂ and the only force on m₂ is F₁, we end up with

$\Delta \vec P_1=-\Delta \vec P_2$

$\Delta \vec P_1+\Delta \vec P_2=0$

$(\vec P_{1f} - \vec P_{1i})+(\vec P_{2f} - \vec P_{2i})=0$

$\vec P_{1i}+ \vec P_{2i}=\vec P_{1f}+\vec P_{2f}$

If we consider the colliding objects forming a system, the equation above indicates that the initial momentum of the system, which is the momentum before collision, is equal to the final momentum of the system, which is the momentum after collision.

$\vec P_{(system)i} =\vec P_{(system)f}$

This means that when the collision takes place the momentum of the system does not change. When a quantity doesn’t change during an event, we say that quantity is conserved. So the equation above is a statement of conservation of momentum in a collision. Notice that conservation of momentum is the direct result of Newton’s Third Law. Also, notice that the following equations are all the same.

Conservation Of Linear Momentum

$\boxed{\Delta\vec P_1+\Delta \vec P_2=0}$

$\boxed{\vec P_{1i}+ \vec P_{2i}=\vec P_{1f}+\vec P_{2f}}$

$\boxed{\vec P_{(system)i} =\vec P_{(system)f}}$

$\boxed{\Delta \vec P_{(system)}=0}$

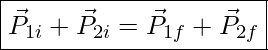
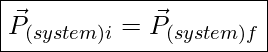
In general, the momentum of a system is conserved only when the net external force on the system is zero. In the example above we assumed the surface was frictionless and the only forces on the two blocks during the collision were the forces that the blocks applied on each other. But even if there was friction and the net external force on the system wasn’t zero, in almost all situations, the force that the colliding objects apply to each other is significantly larger than the friction force or any other external force. This means that we can always use conservation of momentum for collision under any circumstances. We just need to remember that initial momentum is the momentum at the instant before the collision, and final momentum is the momentum immediately after the collision. Finally, we can extend this argument to any number of colliding objects. As long as we take all the colliding objects to be part of our system, we can always use conservation of momentum for that system.

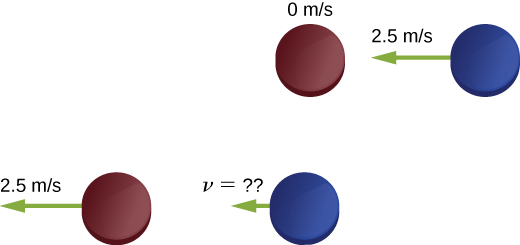
Example 12.5 – Hockey Pucks On Ice

Two hockey pucks of identical mass are on a flat, horizontal ice hockey rink. The red puck is motionless; the blue puck is moving at 2.5 m/s to the left (Figure 12.10). It collides with the motionless red puck. The pucks have a mass of 160 g. After the collision, the red puck is moving at 2.5 m/s, to the left. What is the final velocity of the blue puck?

Solution

We pick the system to consist of the two colliding pucks, and we apply conservation of momentum.

$\vec P_{1i}+ \vec P_{2i}=\vec P_{1f}+\vec P_{2f}$

Momentum is a vector quantity, but in this example all the velocities and therefore momenta are in the horizontal direction. Therefore, we can simply use positive and negative to indicate the direction of these vectors. Let’s take the positive direction to be to the right, and rewrite the equation for conservation of momentum in terms of mass and velocity.

$m_1 \vec v_{1i}+ m_2 \vec v_{2i}=m_1 \vec v_{1f}+m_2 \vec v_{2f}$

In the x-direction

$(0.160kg)(0m/s)+ (0.160kg)(-2.5m/s)=(0.160kg)(-2.5m/s)+(0.160kg)v_{2f}$

$v_{2f}=0$

Discussion

Evidently, the two pucks simply exchanged momentum. The blue puck transferred all of its momentum to the red puck. In fact, this is what happens in a similar collision where m₁ = m₂.

Video Example – Pushing off a skateboard

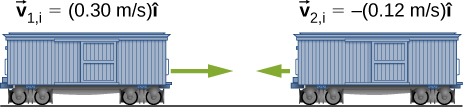
Example 12.6 – Colliding Carts

Two carts in a physics lab roll on a level track, with negligible friction. These carts have small magnets at their ends so that when they collide, they stick together (Figure 12.12). The first cart has a mass of 675 grams and is rolling at 0.750 m/s to the right; the second has a mass of 500 grams and is rolling at 1.33 m/s, also to the right. After the collision, what is the velocity of the two joined carts?

Solution

We pick the system to consist of the two colliding carts, and we apply conservation of momentum.

$\vec P_{1i}+ \vec P_{2i}=\vec P_{1f}+\vec P_{2f}$

Just like example 12.5, this is a one-dimensional situation because all the velocities and momenta are along a straight line. Let’s take the positive direction to be to the right along the x-axis, and rewrite the equation for conservation of momentum in terms of mass and velocity. Since the two carts stick together after the collision, they both move with the same velocity that we can call v_f.

$m_1 \vec v_{1i}+ m_2 \vec v_{2i}=(m_1 + m_2)\vec v_f$

In the x-direction

$(0.675kg)(0.750m/s)+ (0.500kg)(1.33m/s)=(0.675kg + 0.500kg)v_f$

$v_f=0.997m/s$

So, after the collision, the two carts move to the right with a velocity of 0.997m/s.

Video Example – Car hitting a truck and sticking to it

The examples above demonstrate how to apply conservation of momentum to one-dimensional situations, where objects move along a straight line. Now let’s consider two-dimensional situations, like the collision of pool balls on a pool table. The principle is still the same but if velocities have components in both x and y directions, then we have to break up velocity vectors into their components and apply conservation of momentum equation in component form in both x and y directions.

$\vec P_{1i}+ \vec P_{2i}=\vec P_{1f}+\vec P_{2f}$

$(P_{1xi} \hat i + P_{1yi} \hat j) + (P_{2xi} \hat i + P_{2yi} \hat j) = (P_{1xf} \hat i + P_{1yf} \hat j)+ (P_{2xf} \hat i + P_{2yf} \hat j)$

This results in two separate equations; one in the x-direction and the other in the y-direction.

$x-direction$	$y-direction$
$P_{1xi} + P_{2xi} = P_{1xf} + P_{2xf}$	$P_{1yi} + P_{2yi} = P_{1yf} + P_{2yf}$

Example 12.7 – Traffic Collision

A small car of mass 1200 kg traveling east at 60 km/hr collides at an intersection with a truck of mass 3000 kg that is traveling due north at 40 km/hr (Figure 12.13). The two vehicles are locked together. What is the velocity of the combined wreckage?

Solution

The system consists of two cars, and the momentum of this system is conserved when the two cars collide. Since this is a two-dimensional situation, we have to apply the conservation of momentum in both x and y directions. Let’s call the final velocity v_f.

$x-direction$	$y-direction$
$P_{1xi} + P_{2xi} = P_{1xf} + P_{2xf}$	$P_{1yi} + P_{2yi} = P_{1yf} + P_{2yf}$
$m_c v_c + 0 = (m_c + m_T)v_{fx}$	$0+ m_T v_T = (m_c + m_T)v_{fy}$
$(1200kg)(60km/hr) + 0 = (1200kg + 3000)v_{fx}$	$0+ (3000kg)(40km/hr) = (1200kg+3000kg)v_{fy}$
$v_{fx}= 17.1km/hr$	$v_{fy}=28.6km/hr$

Using the components of the final velocity, we can now calculate the magnitude and direction of this vector.

$|\vec v_f|=\sqrt{(17.1km/hr)^2 + (28.6km/hr)^2}$

$|\vec v_f|=33km/hr$

$tan(a)=\frac{28.6km/hr}{17.1km/hr}$

$a=59^\circ$

The final velocity of the wreckage is $\vec v_f=33km/hr @59^\circ$

Notice that since velocity appears on both sides of the equation, we didn’t have to convert km/hr to m/s.

Conservation of momentum simply means that the momentum of the system before and after an event stay the same as demonstrated below.

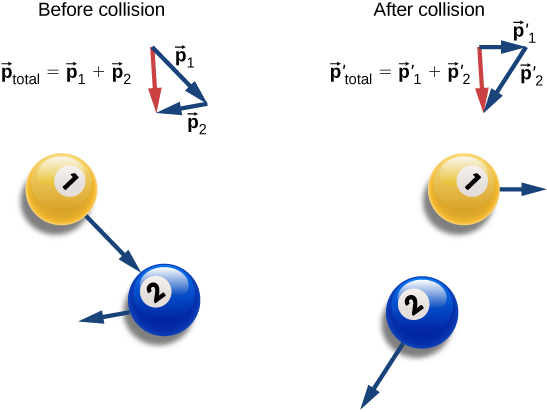
As demonstrated above, the velocity of each ball and therefore the momentum of each ball definitely changes when the collision takes place. But the sum of the momenta of the two balls stays the same before and after the collision.

Video Example – Two-dimensional collision of pucks

Attributions

This chapter contains material taken from Openstax College Physics-Linear Momentum and Collisions, and Openstax University Physics Volume 1 – Linear Momentum and Collisions, and is used under a CC BY 4.0 license, . Download these books for free at Openstax

To see what was changed, refer to the List of Changes.

problems

[openstax univ. phys. vol. 1 – 9.24] What is the magnitude of the average momentum of a 70.0-kg sprinter who runs the 100-m dash in 9.65 s?
[openstax univ. phys. vol. 1 – 9.28] Calculate the final speed of a 110-kg rugby player who is initially running at 8.00 m/s but collides head-on with a padded goalpost and experiences a backward force of 1.76×10⁴N for 5.50×10^-2s.
[openstax univ. phys. vol. 1 – 9.30]A 0.450-kg hammer is moving horizontally at 7.00 m/s when it strikes a nail and comes to rest after driving the nail 1.00 cm into a board. Assume a constant acceleration for the hammer-nail pair.
1. Calculate the duration of the impact.
2. What was the average force exerted on the nail?
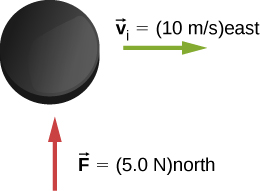
[openstax univ. phys. vol. 1 – 9.33]A hockey puck of mass 150 g is sliding due east on a frictionless table with a speed of 10.0 m/s. Suddenly, a constant force of magnitude 5.00 N and direction due north is applied to the puck for 1.50 s. Find the north and east components of the momentum at the end of the 1.50-s interval.
[openstax univ. phys. vol. 1 – 9.36] Train cars are coupled together by being bumped into one another. Suppose two loaded train cars are moving toward one another, the first having a mass of 1.50×10⁵kg and a velocity of 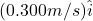$(0.300m/s)\hat i$ and the second having a mass of 1.10×10⁵kg and a velocity of 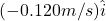$(-0.120m/s)\hat i$ . What is their final velocity?
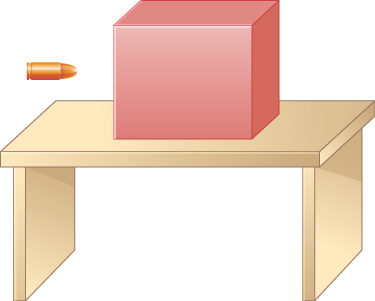
[openstax univ. phys. vol. 1 – 2.47] The figure below shows a bullet of mass 200 g traveling horizontally with a speed of 400 m/s, which strikes a block of mass 1.50 kg that is initially at rest on a frictionless table. After striking the block, the bullet is embedded in the block, and the block and the bullet move together as one unit.
1. What is the magnitude and direction of the velocity of the block/bullet combination immediately after the impact?
2. What is the magnitude and direction of the impulse by the block on the bullet?
3. What is the magnitude and direction of the impulse from the bullet on the block?
4. If it took 3.00ms for the bullet to change its speed from 400 m/s to the final speed after impact, what is the average force between the block and the bullet during this time?
A 20.0-kg child holding a 1.00kg ball is standing on a 3.00-kg skateboard. The child throws the ball horizontally at a speed of 5.00m/s. What is the recoil speed of the child and the skateboard?
A 1.50kg object moving along a straight line with a velocity of 3.00m/s when it experiences a force in the same direction that it is moving. Find the final velocity if the graph of force vs time is
A wooden block with a mass of 3.00kg is at rest on a horizontal table. The coefficient of kinetic friction between the block and the table is 0.200. The block is hit by a bullet with a mass of 40.0g traveling horizontally. The bullet remains in the block after collision. The block, with the bullet inside of it slides a distance of 50.0cm on the table.
1. Find the speed of the block (with the bullet inside) at the moment the block starts to slide.
2. Find the speed of the bullet before it hits the block.
3. Find the the impulse on the bullet.
4. Find the the impulse on the block.