Electrostatics
UNIT 21 – Coulomb’s Law and Electric Field
Last Update: 05/27/2025
Electric charge
You have probably experienced the phenomenon of static electricity: When you first take clothes out of a dryer, many (not all) of them tend to stick together; for some fabrics, they can be very difficult to separate. Another example occurs if you take a woolen sweater off quickly—you can feel (and hear) the static electricity pulling on your clothes, and perhaps even your hair. If you comb your hair on a dry day and then put the comb close to a thin stream of water coming out of a faucet, you will find that the water stream bends toward (is attracted to) the comb.
Many of the characteristics of static electricity can be explored by rubbing things together. Rubbing creates the spark you get from walking across a wool carpet, for example. Static cling generated in a clothes dryer and the attraction of straw to recently polished amber also result from rubbing. Similarly, lightning results from air movements under certain weather conditions. You can also rub a balloon on your hair, and the static electricity created can then make the balloon cling to a wall. We also have to be cautious of static electricity, especially in dry climates. When we pump gasoline, we are warned to discharge ourselves (after sliding across the seat) on a metal surface before grabbing the gas nozzle. Attendants in hospital operating rooms must wear booties with aluminum foil on the bottoms to avoid creating sparks that may ignite the oxygen being used.
Some of the most basic characteristics of static electricity include:
- The effects of static electricity are explained by a physical quantity not previously introduced, called electric charge.
- There are only two types of charge, one called positive and the other called negative.
- Like charges repel, whereas unlike charges attract.
- The force between charges decreases with distance.
How do we know there are two types of electric charge? When various materials are rubbed together in controlled ways, certain combinations of materials always produce one type of charge on one material and the opposite type on the other. By convention, we call one type of charge “positive”, and the other type “negative.” For example, when glass is rubbed with silk, the glass becomes positively charged and the silk negatively charged. Since the glass and silk have opposite charges, they attract one another like clothes that have rubbed together in a dryer. Two glass rods rubbed with silk in this manner will repel one another, since each rod has a positive charge on it. Similarly, two silk cloths so rubbed will repel, since both cloths have a negative charge.
Figure 20.1 shows a simple model of an atom with negative electrons orbiting its positive nucleus. The nucleus is positive due to the presence of positively charged protons. Nearly all charge in nature is due to electrons and protons, which are two of the three building blocks of most matter. (The third is the neutron, which is neutral, carrying no charge.) Other charge-carrying particles are observed in cosmic rays and nuclear decay and are created in particle accelerators. All but the electron and proton survive only a short time and are quite rare by comparison. An atom has an equal number of protons and electrons. Electrons carry the charge we have named negative. Protons carry an equal-magnitude charge that we call positive.

The charges of electrons and protons are identical in magnitude but opposite in sign. Therefore, an atom, as a whole, is electrically neutral. Usually, charges are formed by combinations of electrons and protons. The magnitude of this basic charge is
Electrons can be separated from the atom—for example, by rubbing materials together. Some atoms and molecules have a greater affinity for electrons than others and will become negatively charged by close contact in rubbing, leaving the other material positively charged.
No charge is actually created or destroyed when charges are separated as we have been discussing. Rather, existing charges are moved about. In fact, in all situations the total amount of charge is always constant. This universally obeyed law of nature is called the law of conservation of charge.
conductors and insulators
Some substances, such as metals and salty water, allow charges to move through them with relative ease. Some of the electrons in metals and similar conductors are not bound to individual atoms or sites in the material. These free electrons (conduction electrons) can move through the material much as air moves through loose sand. Any substance that has free electrons and allows charge to move relatively freely through it is called a conductor. The moving electrons may collide with fixed atoms and molecules, losing some energy, but they can move in a conductor. Superconductors allow the movement of charge without any loss of energy. Salty water and other similar conducting materials contain free ions that can move through them. An ion is an atom or molecule that has lost or gained additional electron(s), and as a result, it has a positive or negative (nonzero) total charge. In other words, in an ion, the total number of electrons is not equal to the total number of protons.
Other substances, such as glass, do not allow charges to move through them. These are called insulators. Electrons and ions in insulators are bound in the structure and cannot move easily. Pure water and dry table salt are insulators, whereas molten salt and salty water are conductors.
polarization of charge
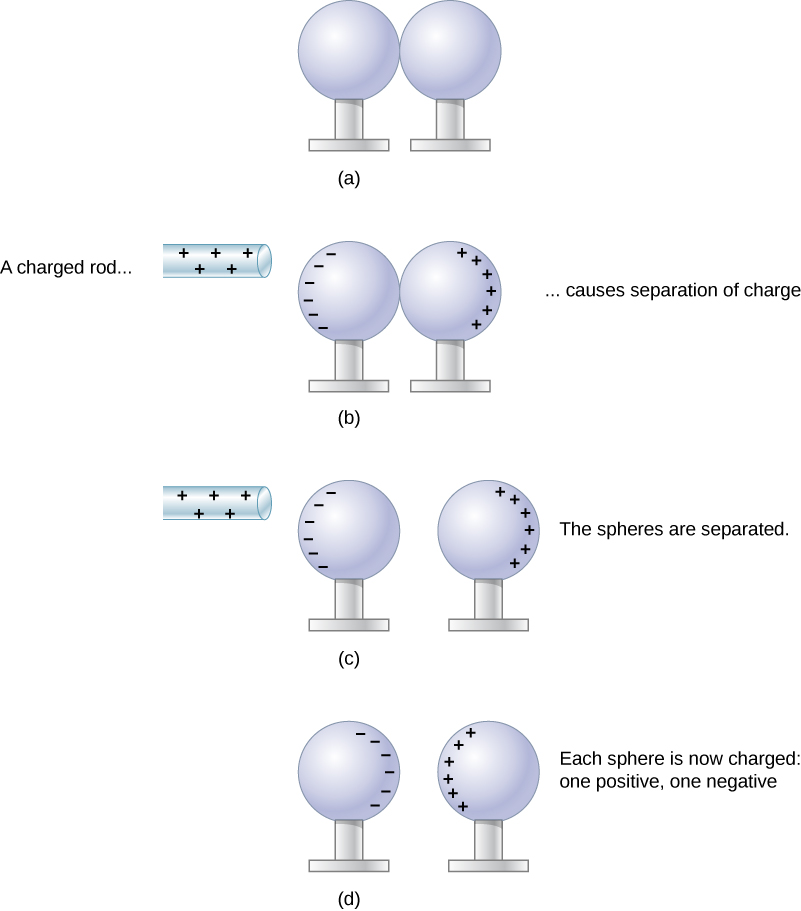
Let’s examine in more detail what happens in a conductor when an electrically charged object is brought close to it. As mentioned, the conduction electrons in the conductor are able to move with nearly complete freedom. As a result, when a charged insulator (such as a positively charged glass rod) is brought close to the conductor, the (total) charge on the insulator exerts an electric force on the conduction electrons. Since the rod is positively charged, the conduction electrons (which themselves are negatively charged) are attracted, flowing toward the insulator to the near side of the conductor. This is shown in Figure 20.2

Now, the conductor is still overall electrically neutral; the conduction electrons have changed position, but they are still in the conducting material. However, the conductor now has a charge distribution; the near end (the portion of the conductor closest to the insulator) now has more negative charge than positive charge, and the reverse is true of the end farthest from the insulator. The relocation of negative charges to the near side of the conductor results in an overall positive charge in the part of the conductor farthest from the insulator. We have thus created an electric charge distribution where one did not exist before. This process is referred to as inducing polarization—in this case, polarizing the conductor. The resulting separation of positive and negative charge is called polarization, and the material, or even the molecule, that exhibits polarization is said to be polarized.
Neutral objects can be attracted to any charged object. The pieces of straw attracted to polished amber are neutral, for example. If you run a plastic comb through your hair, the charged comb can pick up neutral pieces of paper. Figure 20.3 shows how the polarization of atoms and molecules in neutral objects results in their attraction to a charged object.

ways to transfer electrostatic charge to various materials (charging)
When a charged object comes in contact with a neutral object, some of the charges are transferred to the neutral object. This is called charging by contact.
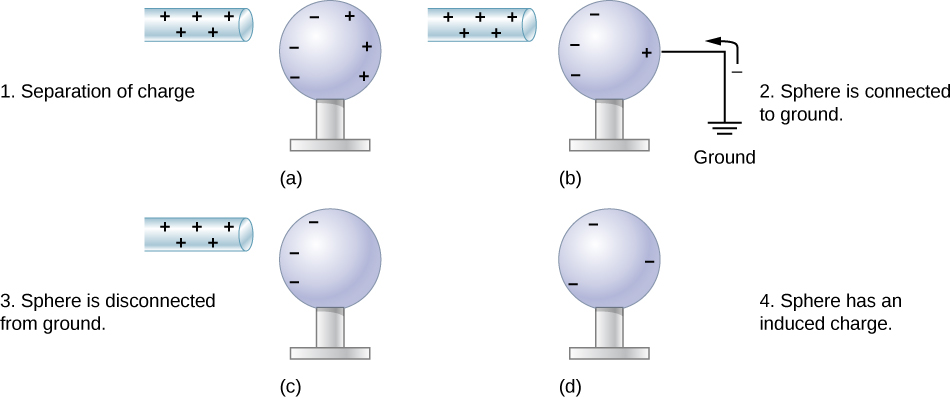
But there is another way to transfer charge from one object to a neutral conductor, without any direct contact between the charged object and the conductor. This is called charging by induction. The process of charging by induction is demonstrated in Figure 20.4.
Here are some cool things you can try yourself to see the interactions between charged objects.
coulomb’s law
Experiments with electric charges have shown that if two point objects each have an electric charge, then they exert an electric force on each other. The magnitude of the force is directly proportional to the net charge on each point object and inversely proportional to the square of the distance between them. The direction of the force vector is along the imaginary line joining the two point-objects and is dictated by the signs of the charges involved. These relationships are represented by the following equation known as Coulomb’s Law.
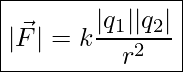 Coulomb’s Law
Coulomb’s Law
In this equation
![]() is the magnitude of the electric force between the two point-objects
is the magnitude of the electric force between the two point-objects
![]() is the magnitude of the charge of one point object
is the magnitude of the charge of one point object
![]() is the magnitude of the charge of the other point object
is the magnitude of the charge of the other point object
![]() is the distance between the two point-objects
is the distance between the two point-objects
![]() is a constant, called Coulomb’s constant,
is a constant, called Coulomb’s constant, ![]()
The direction of the force between the two point-charges depends on the type of charges that are interacting. Like charges repel, and unlike charges attract as shown in Figure 20.6

Example 20.1
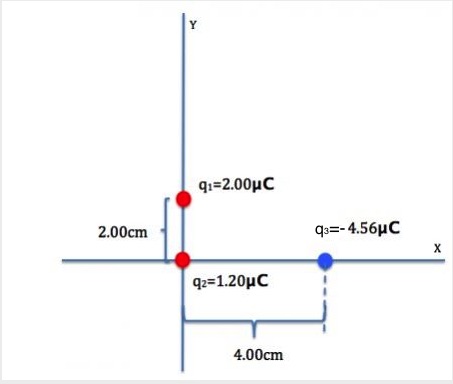
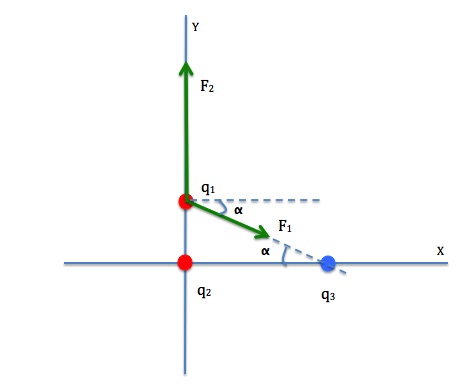
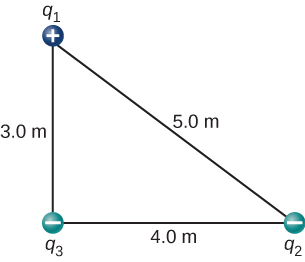
Three point-charges are placed as shown in Figure 20.7. Determine the magnitude and direction of the net force on q1.
 |
 |
Solution
We need to use Coulomb’s law to find the force on q1 by q2, and the force on q1 by q3 and add them together using the method of vector addition.
Let’s label the force on q1 by q2 as ![]() and the distance between them as r2.
and the distance between them as r2.
![]()
![]()
![]()
Let’s label the force on q1 by q3 as ![]() and the distance between them as r1.
and the distance between them as r1.
We can use Pythagorean Theorem to find (r1 )2.
![]()
![]()
Now we can calculate ![]()
![]()
![]()
![]()
To add the two forces we must break them up into components and add the components. For a review of the analytical method of vector addition, see UNIT 4.
Let’s first calculate the angle ![]() .
. ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
Let’s now find the magnitude and direction of the net force, ![]()

![]()
![]()
Finally, we determine the direction of the resultant force by finding Θ, the angle ![]() makes with the horizontal axis.
makes with the horizontal axis.
![]()
![]()
![]()
Therefore the net force on q1 is ![]()
Electric Forces In Biology
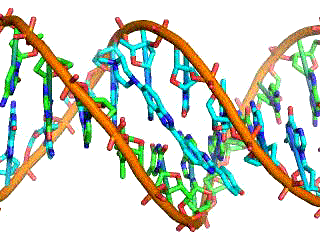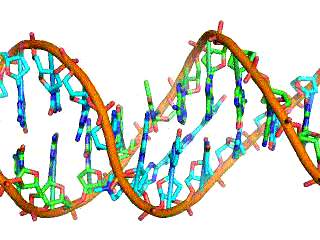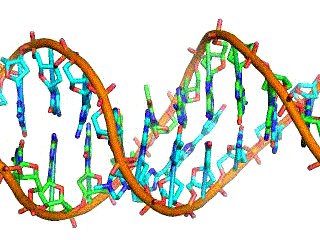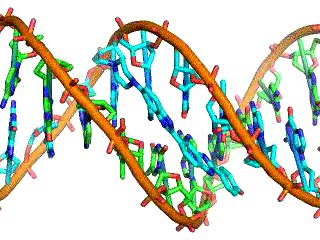
Classical electrostatics has an important role to play in modern molecular biology. Large molecules such as proteins, nucleic acids, and so on—so important to life—are usually electrically charged. DNA itself is highly charged; it is the electrostatic force that not only holds the molecule together but gives the molecule structure and strength. The figure below is a schematic of the DNA double helix.
The four nucleotide bases are given the symbols A (adenine), C (cytosine), G (guanine), and T (thymine). The order of the four bases varies in each strand, but the pairing between bases is always the same. C and G are always paired and A and T are always paired, which helps to preserve the order of bases in cell division (mitosis) so as to pass on the correct genetic information. Since the Coulomb force drops with distance, the distances between the base pairs must be small enough that the electrostatic force is sufficient to hold them together.
DNA is a highly charged molecule, with about 2e (fundamental charge) per 0.3nm. The distance separating the two strands that make up the DNA structure is about 1 nm, while the distance separating the individual atoms within each base is about 0.3 nm.
One might wonder why electrostatic forces do not play a larger role in biology than they do if we have so many charged molecules. The reason is that the electrostatic force is “diluted” due to screening between molecules. This is due to the presence of other charges in the cell.
The polarity of Water Molecules
The best example of this charge screening is the water molecule, represented as H2O. Water is a strongly polar molecule. Its 10 electrons (8 from the oxygen atom and 2 from the two hydrogen atoms) tend to remain closer to the oxygen nucleus than the hydrogen nuclei. This creates two centers of equal and opposite charges—what is called a dipole, as illustrated below. The magnitude of the dipole is called the dipole moment.

These two centers of charge will terminate some of the electric field lines coming from a free charge, as on a DNA molecule. This results in a reduction in the strength of the Coulomb interaction. One might say that screening makes the Coulomb force a short-range force rather than long-range.
Other ions of importance in biology that can reduce or screen Coulomb interactions are <span id=”MathJax-Element-19-Frame” class=”MathJax” style=”overflow: initial;font-style: normal;font-weight: normal;line-height: normal;font-size: 14px;text-indent: 0px;text-align: left;text-transform: none;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;padding: 0px;margin: 0px” role=”presentation” data-mathml=”
Na+,Na+,”>Na+, and <span id=”MathJax-Element-20-Frame” class=”MathJax” style=”overflow: initial;font-style: normal;font-weight: normal;line-height: normal;font-size: 14px;text-indent: 0px;text-align: left;text-transform: none;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;padding: 0px;margin: 0px” role=”presentation” data-mathml=”
K+,K+,”>K+, and <span id=”MathJax-Element-21-Frame” class=”MathJax” style=”overflow: initial;font-style: normal;font-weight: normal;line-height: normal;font-size: 14px;text-indent: 0px;text-align: left;text-transform: none;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;padding: 0px;margin: 0px” role=”presentation” data-mathml=”
Cl–Cl–”>Cl–. These ions are located both inside and outside of living cells. The movement of these ions through cell membranes is crucial to the motion of nerve impulses through nerve axons.
Recent studies of electrostatics in biology seem to show that electric fields in cells can be extended over larger distances, in spite of screening, by “microtubules” within the cell. These microtubules are hollow tubes composed of proteins that guide the movement of chromosomes when cells divide, the motion of other organisms within the cell, and provide mechanisms for the motion of some cells (as motors).
Electric field
We know electric charges interact with one another without any contact. For example, a positively charged glass rod attracts a negatively charged acrylic rod from a distance. The concept of an electric field helps us explain how the two charged objects can interact without any physical contact.
Consider a point charge that we are going to call a “source charge”, and represent with Q. This source charge creates an electric field around it. You can think of this electric field as being a disturbance in space that surrounds the source charge (hence the name source charge, because this particular point charge is the source of the electric field we are considering). If we bring in another point charge, which we are going to call the test charge, and represent with q, and place it in the electric field of the source charge, that test charge is going to experience a force. This is the same Coulomb Force we discussed earlier. We can think of it this way: the test charge q interacts with the electric field of the source charge, Q, and this interaction manifests itself in the form of a force on the test charge.
the electric field of a point charge
The electric field is a vector quantity. In this section, we discuss how to determine the magnitude and direction of the electric field of a single point-charge.
The electric field is defined as the ratio of the Coulomb force to the test charge:
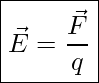 Definition of Electric Field
Definition of Electric Field
If the electric field is due to a point charge Q, the force on the test charge, calculated by using Coulomb’s law, is given by ![]() . Therefore, the magnitude of the electric field at a point in space in the vicinity of a source charge, Q, is
. Therefore, the magnitude of the electric field at a point in space in the vicinity of a source charge, Q, is
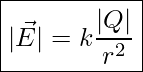 Eelectric Field of A Point Charge
Eelectric Field of A Point Charge
In this equation
![]() is the source charge creating the electric field
is the source charge creating the electric field ![]() .
.
![]() is the distance between the source charge and the point in space where we are calculating the magnitude of the electric field.
is the distance between the source charge and the point in space where we are calculating the magnitude of the electric field.
![]() is a constant, called Coulomb’s constant,
is a constant, called Coulomb’s constant, ![]()
The direction of the electric field at that point is the same as the direction of the force that the source charge, Q, would apply on a positive test charge placed at that point. This means that the direction of the electric field around a positive source charge points radially outward, while the electric field of a negative source charge points radially inward.
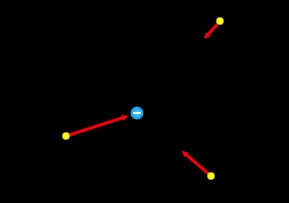
Figure 20.11 and Figure 20.12 show the electric field vectors at several points around a positive and negative source charge respectively. Notice how the electric field gets weaker at points farther away from the source charge.
 |
 |
You can explore the magnitude and direction of the electric field at various points in space around positive and negative charges using the simulation below.
Rearranging the equation that defines the electric field we get
![]() Force On Charge q Placed In An External Electric Field
Force On Charge q Placed In An External Electric Field
This equation is very useful because it means that if we know the electric field at a point in space (whether it is created by one source charge or many source charges), we can determine the force on any charge, q, placed at that point.
Example 20.2
A point charge of 2.00nC is placed at the origin of a coordinate system.
a) Calculate the strength and direction of the electric field due to this charge at point P(2.00mm, 4.00mm)
b) What force does the electric field found in (a) exert on a point charge of –0.250μC?

Solution for (a)
Since the source charge is positive, the electric field at point P is a vector pointing away from the source charge, as shown in Figure 20.16.
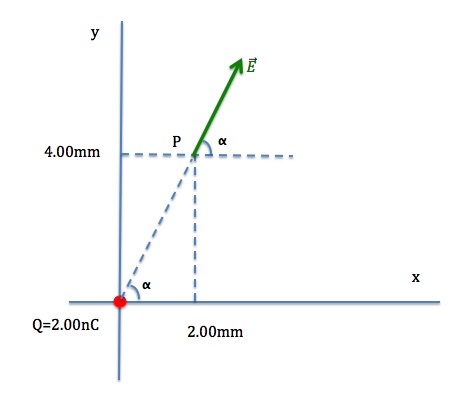
The magnitude of this electric field is given by
![]()
![]()
![]()
We need to find the angle α to specify the direction of the electric field.
![]()
![]()
The electric field at point P is ![]()
Solution for (b)
There are two ways to answer this question. One way is to use Coulomb’s law (![]() ) to calculate the force between the two charges. But since we have already determined the electric field of Q at point P, a much easier way is to use this electric field to find the force on q=–0.250μC.
) to calculate the force between the two charges. But since we have already determined the electric field of Q at point P, a much easier way is to use this electric field to find the force on q=–0.250μC.
![]()
Since the charge that is placed in the electric field is negative, the direction of the force on it is opposite to the direction of the electric field, and its magnitude is
![]()
![]()
To get the direction of this force, we need to find Θ.
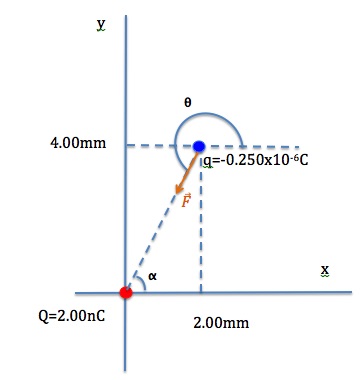
![]()
![]()
![]()
The force on charge q is![]()
the electric field of multiple-point charges
The total electric field created by multiple charges is the vector sum of the individual fields created by each charge. The following example shows how to add electric field vectors.
Example 20.3
Point charge q1=5.00nC is at (0, – 2.00cm), and point charge q2 = 10.0nC is at (4.00cm, 0). Find the magnitude and direction of the total electric field due to the two point-charges at the origin of the coordinate system.
Solution
We need to find the electric field due to each charge separately, and then add the two vectors together to get the total electric field.
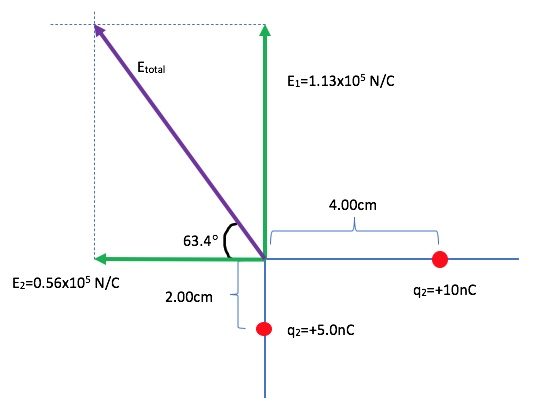
The electric field due to q1 is
![]()
![]()
![]()
The electric field due to q2 is
![]()
![]()
![]()
Now we have to add the two vectors
![]()
![]()
We can leave the answer in component form as follows:
![]()
Or, we can find the magnitude and direction of ![]()
![]()
![]()
Let’s call the angle ![]() makes with the negative x-axis Θ.
makes with the negative x-axis Θ.
![]()
![]()
So the angle relative to the positive x-axis is
![]()
Therefore, in terms of magnitude and direction, ![]() is
is
![]()
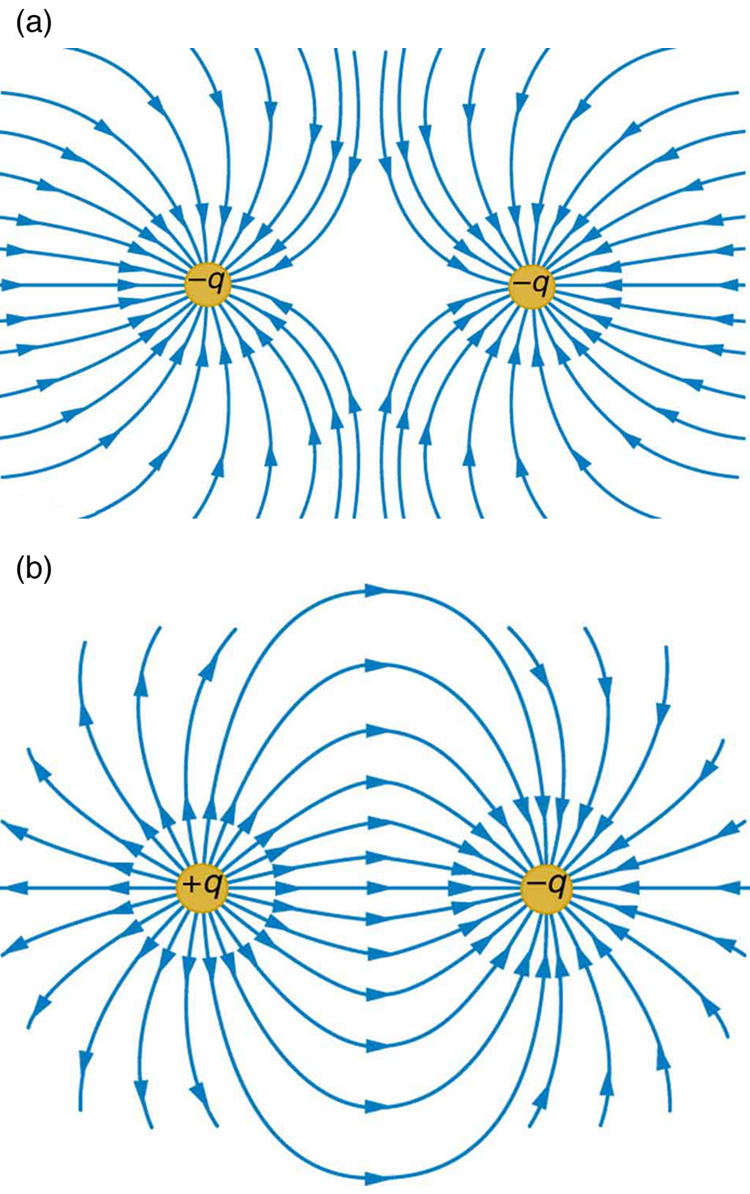
Figure 20.19 shows how the electric field from two point-charges can be drawn by finding the total field at representative points and drawing electric field lines consistent with those points. While the electric fields from multiple charges are more complex than those of single charges, some simple features are easily noticed.
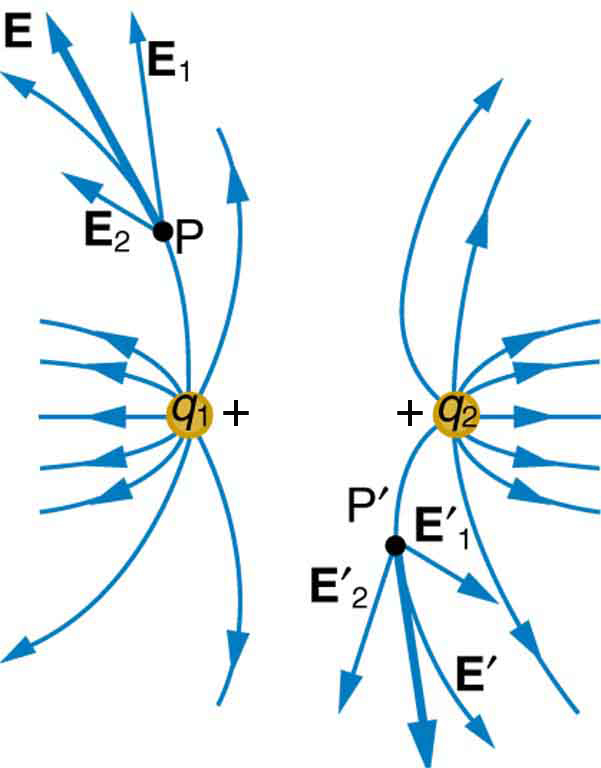
For example, the field is weaker between like charges, as shown by the lines being farther apart in that region. This is because the fields from each charge exert opposing forces on any charge placed between them. See Figure 20.20(a) and (b). Furthermore, at a great distance from two like charges, the field becomes identical to the field from a single, larger charge.
- Field lines must begin on positive charges and terminate on negative charges, or at infinity in the hypothetical case of isolated charges.
- The number of field lines leaving a positive charge or entering a negative charge is proportional to the magnitude of the charge.
- The strength of the field is proportional to the closeness of the field lines—more precisely, it is proportional to the number of lines per unit area perpendicular to the lines.
- The direction of the electric field is tangent to the field line at any point in space.
- Field lines can never cross.
The last property means that the field is unique at any point. The field line represents the direction of the field; so if they crossed, the field would have two directions at that location (an impossibility if the field is unique).
Applications of electric field
Gel Electrcophoresis
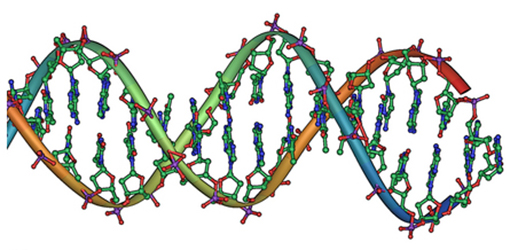
DNA is a highly charged molecule. It is the electrostatic force that not only holds the molecule together but gives the molecule structure and strength.Figure 21.11 is a schematic of the DNA double helix.
Gel electrophoresis is a technique used to separate DNA fragments of different sizes. The DNA is loaded on the gel and an electric current is applied. The DNA has a net negative charge and moves from the negative electrode toward the positive electrode. The electric current is applied for sufficient time to let the DNA separate according to size; the smallest fragments will be farthest from the well (where the DNA was loaded), and the heavier molecular weight fragments will be closest to the well. Once the DNA is separated, the gel is stained with a DNA-specific dye for viewing it.
Xerography
Most copy machines use an electrostatic process called xerography—a word coined from the Greek words xeros for dry and graphos for writing. The heart of the process is shown in simplified form below.

A selenium-coated aluminum drum is sprayed with a positive charge from points on a device called a corotron. Selenium is a substance with an interesting property—it is a photoconductor. That is, selenium is an insulator when in the dark and a conductor when exposed to light.
In the first stage of the xerography process, the conducting aluminum drum is grounded so that a negative charge is induced under the thin layer of uniformly positively charged selenium. In the second stage, the surface of the drum is exposed to the image of whatever is to be copied. Where the image is light, the selenium becomes conducting, and the positive charge is neutralized. In dark areas, the positive charge remains, and so the image has been transferred to the drum.
The third stage takes a dry black powder, called toner, and sprays it with a negative charge so that it will be attracted to the positive regions of the drum. Next, a blank piece of paper is given a greater positive charge than the drum so that it will pull the toner from the drum. Finally, the paper and electrostatically held toner are passed through heated pressure rollers, which melt and permanently adhere the toner within the fibers of the paper.
Laser Printers
Laser printers use the xerographic process to make high-quality images on paper, employing a laser to produce an image on the photo-conducting drum as shown below. In its most common application, the laser printer receives output from a computer, and it can achieve high-quality output because of the precision with which laser light can be controlled. Many laser printers do significant information processing, such as making sophisticated letters or fonts, and may contain a computer more powerful than the one giving them the raw data to be printed.

Ink Jet Printers and Electrostatic Painting
The inkjet printer, commonly used to print computer-generated text and graphics, also employs electrostatics. A nozzle makes a fine spray of tiny ink droplets, which are then given an electrostatic charge.
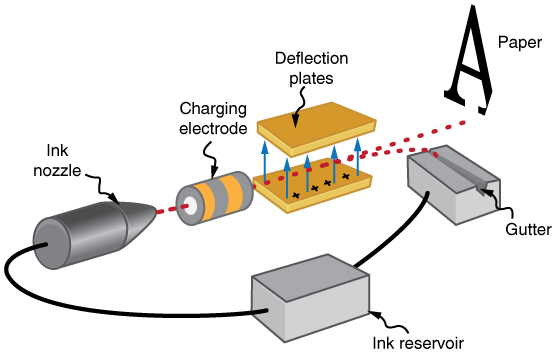
Once charged, the droplets can be directed, using pairs of charged plates, with great precision to form letters and images on paper. Inkjet printers can produce color images by using a black jet and three other jets with primary colors, usually cyan, magenta, and yellow, much as a color television produces color. (This is more difficult with xerography, requiring multiple drums and toners.)
Smoke Precipitators and Electrostatic Air Cleaning
Another important application of electrostatics is found in air cleaners, both large and small. The electrostatic part of the process places an excess (usually positive) charge on smoke, dust, pollen, and other particles in the air and then passes the air through an oppositely charged grid that attracts and retains the charged particles.
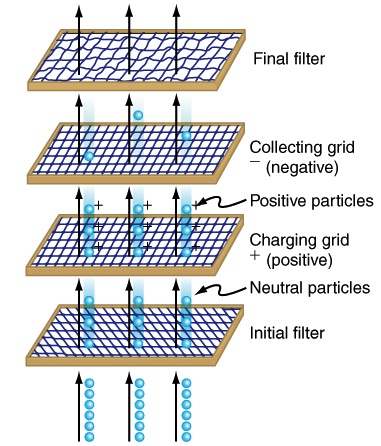
Large electrostatic precipitators are used industrially to remove over 99% of the particles from stack gas emissions associated with the burning of coal and oil. Home precipitators, often in conjunction with the home heating and air conditioning system, are very effective in removing polluting particles, irritants, and allergens.
Attribution
This chapter contains material taken from Openstax College Physics-Electric Charge and Electric Field, and Openstax University Physics Volume 2-Electric Charges and Fields, and is used under a CC BY 4.0 license. Download these books for free at Openstax
To see what was changed, refer to the List of Changes.
questions and PROBLEMS
questions
- [openstax college phys. quest18.1] There are very large number of charged particles in all objects. Why, then, don’t most objects exhibit static electricity?
- [openstax college phys. quest18.2] Why do most objects tend to contain nearly equal numbers of positive and negative charges?
- [openstax college phys. quest18.5 modifed] When a glass rod is rubbed with silk, it becomes positive and the silk becomes negative – yet both attract dust. Explain why dust particles are attracted to both positive and negative charges.
- [openstax college phys. quest18.7] Describe how a positively charged object can be used to give another object a negative charge. What is the name of this process?
- Explain why polar molecules, like the molecules of water, are attracted to both positive and negative charges
- [openstax univ. phys. vol.2 quest5.3] A positively charged rod attracts a small piece of cork.
- Can we conclude that the cork is negatively charged?
- The rod repels another piece of cork. Can we conclude that this piece is positively charged?
- [openstax univ. phys. vol.2 quest5.9] Does the uncharged conductor shown below experience a net electric force? Justify your answer.
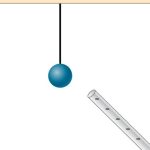
- [openstax univ. phys. vol.2 quest5.10]While walking on a rug, a person frequently becomes charged because of the rubbing between their shoes and the rug. This charge then causes a spark and a slight shock when the person gets close to a metal object. Why are these shocks so much more common on dry days?
- [openstax univ. phys. vol.2 quest5.11] Compare charging by conduction and charging by induction.
- [openstax college phys. quest18.12] Why must the test charge in the definition of the electric field be vanishingly small?
- [openstax college phys. quest18.15] The figure shows an electric field extending over three regions, labeled I, II, and III. Answer the following questions.
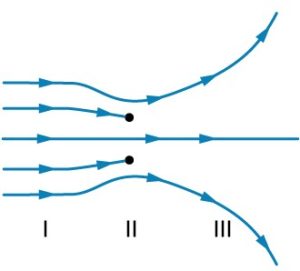
fig-quest20.11 [Image Description] - Are there any isolated charges? If so, in what region and what are their signs?
- Where is the field strongest/weakest? Explain your reasoning.
- Where is the field the most uniform? Explain your reasoning.
- [openstax univ. phys. vol2 quest5.25] If the electric field at a point on the line between two charges is zero, what do you know about the charges?
- [openstax univ. phys. vol2 quest5.26] Two charges lie along the x-axis. Is it true that the net electric field always vanishes at some point (other than infinity) along the x-axis?
- [openstax univ. phys. vol2 quest5.35] What is the ratio of the number of electric field lines leaving a charge 10q and a charge q?
- How can we draw diagrams to show the magnitude and direction of the electric field in a region using electric field lines?
- What factors determine the magnitude and direction of the force on a point charge placed in an electric field?
problems
- [openstax univ. phys. vol.2 – 5.41 – modified] A 2.50-g copper penny is given a charge of -2.00×10-9C.
- How many excess electrons are on the penny?
- What is the mass of the excess electrons on the penny?
- [openstax univ. phys. vol. 2 – 5.45]A 50.0-g ball of copper has a net charge of 2.00μC. What fraction of the copper’s electrons has been removed? (Each copper atom has 29 protons, and copper has an atomic mass of 63.5.)
- [openstax univ. phys. vol. 2 – 5.49] Two charges+3.00μC and +12.0μC are fixed 1.00 m apart, with the second one to the right. Find the magnitude and direction of the net electrostatic force on a −2.00nC charge when placed at the following locations.
- Halfway between the two.
- Half a meter to the left of the +3.00μC charge.
- Half a meter above the +12.0μC charge in a direction perpendicular to the line joining the two fixed charges.
- [openstax univ. phys. vol. 2 – 5.50] In a salt crystal, the distance between adjacent sodium and chloride ions is 2.82×10-10m. What is the force of attraction between the two singly charged ions?
- [openstax univ. phys. vol.2 – 5.55] Two small balls, each of mass 5.00 g, are attached to silk threads 50.0 cm long, which are in turn tied to the same point on the ceiling, as shown below. When the balls are given the same charge Q, the threads hang at 5.00º to the vertical, as shown below. What is the magnitude of Q? What are the signs of the two charges?

fig-prob20.5 [Image Description] - [openstax univ. phys. vol. 2 – 5.60 – modified] In the configuration below, q=3.00nC, and a=4.00cm. What is the net electrostatic force on the charge located at the lower right-hand corner of the triangle shown here?
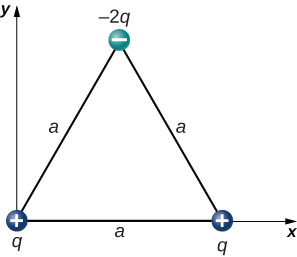
- [openstax univ. phys. vol. 2 – 5.62]The charges q1=2.00×10-7C, q2=-4.00×10-7C, and q3=-1.00×10-7C are placed at the corners of the triangle shown below. What is the net electrostatic force on q1?
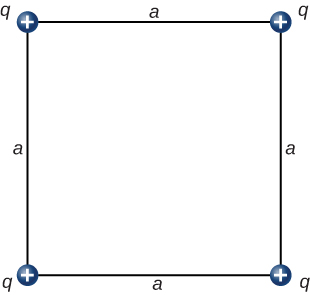
- [openstax univ. phys. vol. 2 – 5.63 – modified] In the configuration below, q=8.00μC and a=5.00cm. What is the net electrostatic force on the charge q at the lower-right-hand corner of the square shown here?
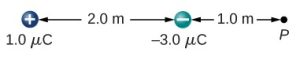
- [openstax univ. phys. vol. 2 – 5.59] A charge q=2.0μC is placed at the point P shown below. What is the force on q?
- [openstax univ. phys. vol. 2 – 5.109] What is the force on the 5.0μC charge shown below?
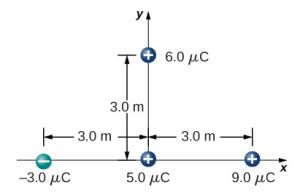
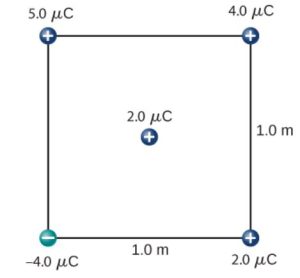
fig-prob20.10 [Image Description] - [openstax univ. phys. vol. 2 – 5.110] What is the force on the 2.0 μC charge placed at the center of the square shown below?
- A point charge of q1=16.0nC is placed at the origin and a point charge of q2=31.0nC is placed at x=10.0cm.
- Where would a third charge of q3= -15.0nC be in equilibrium along the x-axis?
- Where would a third charge q3= -15.0nC be in equilibrium along the x-axis if q1=-16.0nC?
- [openstax univ. phys. vol.2 – 5.65] A particle of charge 2.00×10-8C experiences an upward force of magnitude 4.00×10-6N when it is placed at a particular point in an electric field.
- What is the electric field at that point?
- If a charge q=-1.00×10-8C is placed there, what is the force on it?
- [openstax univ. phys. vol. 2 – 5.67 – modified] Consider an electron that is 1.00×10-10m to the left of an alpha particle as shown. An alpha particle consists of two protons and two neutrons that are tightly bound together. Therefore, the electric charge of an alpha particle is 3.20×10-19C).

- What is the electric field due to the alpha particle at the location of the electron? Draw a vector to show this electric field and label it as
 .
. - What is the electric field due to the electron at the location of the alpha particle? Draw a vector to show this electric field and label it as
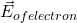 .
. - What is the electric force on the alpha particle? Show this force with a vector labeled as
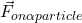 .
. - What is the electric force on the electron? Show this force with a vector labeled as
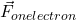 .
.
- What is the electric field due to the alpha particle at the location of the electron? Draw a vector to show this electric field and label it as
- [openstax univ. phys. vol. 2 – 5.72] A small piece of cork whose mass is 2.00 g is given a charge of 5.00×10-7C. What electric field is needed to place the cork in equilibrium under the combined electric and gravitational forces?
- [openstax univ. phys. vol. 2 – 2.73] If the electric field of a point charge q is 100N/C at a distance of 50.0 cm from it. What is the value of q?
- [openstax univ. phys. vol. 2 – 5.76 – modified] Two point charges, q1=2.00×10-7C and q2=-6.00×10-8C are held 25.0 cm apart, with q1 to the left of q2.
- What is the magnitude and direction of the electric field at a point between the two charges and 5.00 cm from q1?
- What is the magnitude and direction of the force on an electron placed at that point?
- [openstax univ. phys. vol.2 – 5.79] Point charges q1=q2=4.00×10-6C are fixed on the x-axis at x=-3.00m and x=3.00m. What charge q must be placed at the origin so that the electric field vanishes at x=0, y=3.00m?
- [openstax unv. phys. vol. 2 – 5.91] A proton moves in the electric field
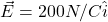
- Determine the force on the proton and its acceleration.
- Do the same calculation for an electron moving in this field.
- [openstax univ. phys. vol. 2 – 5.92] An electron and a proton, each starting from rest, are accelerated by the same uniform electric field of 200 N/C. Determine the distance and time for each particle to acquire kinetic energy of 3.20×10-16J.
- [openstax univ. phys. vol. 2 – 5.93] A spherical water droplet of radius 25.0μm carries an excess of 250 electrons. What vertical electric field (magnitude and direction) is needed to balance the gravitational force on the droplet?
- [openstax univ. phys. vol. 2 – 5.94] A proton enters the uniform electric field produced by the two charged plates shown below. The magnitude of the electric field is 4.00×105 N/C, and the speed of the proton when it enters is 1.50×107m/s. What distance d has the proton been deflected downward when it leaves the plates?
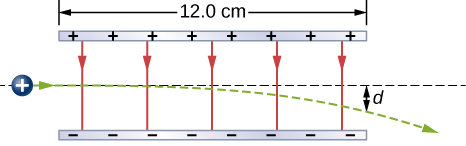
fig-prob20.22 [Image Description] - [openstax college phys. 18.60] A 5.00 g charged insulating ball hangs on a 30.0 cm long string in a uniform horizontal electric field as shown below. Given the charge on the ball is 1.00μC, find the strength of the field.

- Four point-charges are held at the corners of a square as shown.
- Determine the magnitude and direction of the electric field in the center of the square.
- Determine the magnitude and direction of the force experienced by a 2.00µC charge placed at the center of the square.
- Determine the magnitude and direction of the force experienced by a -2.00µC charge placed at the center of the square.
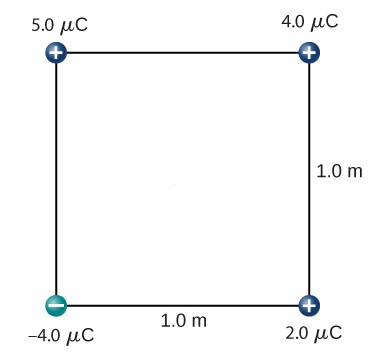
image descriptions
fig-prob20.5 image description – 2 point charges Q are attached to equal-length strings hanging from the same point on the ceiling. The charges repel each other. The angle between on string and the vertical is 5 degrees. [Return to the image]
fig-prob20.10 image description – A 5.0μC point charge is at the origin. a -3.0μC point charge is 3.0m to its left on the x-axis. A 9.0μC point charge is 3.0m to its right on the x-axis. A 6.0μC point charge is 3.0m above it on the y-axis. [Return to the image]
fig-quest20.11 image description – Five electric field lines are pointing to the right. In Region I, all five lines are parallel and equal distance apart. In region II the top line dips down and then continues deflecting upward and away from the horizontal line in region III. The line below it ends at a point. The middle line continues straight. The next one below it ends at a point. The last one curves up and then continues deflecting downward and away from the horizontal line in Region III. In Region III, the top line deflects upward and away from the horizontal, the middle line is straight and horizontal, and the line at the bottom deflects downward and away from the horizontal. [Return to the image]
fig-prob20.22 image description – A positive charge is deviated by a distance d from its horizontal path as it moves through a uniform vertical electric field between two oppositely charged plates. The electric field points downward. [Return to the image]