Unit 17 – Ideal Gas Law and Kinetic Theory

Beta Keramati

Fluids

Unit 17 – Ideal Gas Law and Kinetic Theory

Last Update: 05/24/2025

ideal gas law

In this section, we explore the behavior of gases. Gases are fluids but unlike liquids, they don’t have a set volume and fill the volume of the container they are in. Unlike liquids, gases are compressible. This property is due to the large separation of atoms and molecules in gases, compared to their size. If the temperature of a gas is not too high and/or its pressure too low, it is safe to assume the separation between molecules is so large that all forces between them except for collision forces can be ignored. In contrast, in liquids and solids, atoms and molecules are closer together and the forces between them are stronger.

An ideal gas is an idealized model of how a gas behaves. In this model, an ideal gas is a gas that consists of molecules with separation distances much larger than their size. Furthermore, according to this model, these molecules interact only when they collide, and the collisions between the molecules and the molecules and the walls of the container are all elastic. The ideal gas model is very useful because it correctly predicts the behavior of all gases in most situations. In this book, we will only discuss the behavior of gases as described by the ideal gas model.

The relationship between pressure, volume, temperature, and the number of molecules of an ideal gas was first found experimentally and is known as the Ideal Gas Law.

$\boxed{PV=Nk_BT}$ Ideal Gas Law

In this equation,

$P$ is the absolute pressure ( $Pressure=\frac{force}{volume}$ ), and is measured in units of Pascal (Pa). Pa=N/m³

$V$ is the volume which is the amount of space the gas occupies and is measured in units of m³

$N$ is the number of molecules of gas

$k_B$ is the Boltzmann Constant. $k_B= 1.38\times 10^{-23}J/K$

$T$ is the absolute temperature of the gas in Kelvin

Example 17.1 – Tire Pressure

Suppose your bicycle tire is fully inflated, with an absolute pressure of 7.00×10⁵Pa, at a temperature of 18.0°C. What is the pressure after its temperature has risen to 35.0°C? Assume that there are no appreciable leaks or changes in volume.

Solution

We know that P₁=7.00×10⁵Pa at a temperature of T₁=18.0°C. We are trying to find P₂ at a temperature of T₂=35.0°C. As the gas transitions from state (1) to state (2) its number of molecules and volume stay constant.

For each state, we can relate P, T, V, and N using the ideal gas law.

$P_1V_1=N_1k_BT_1$

$P_2V_2=N_2k_BT_2$

Since volume and number of molecules don’t change, we don’t need to use a subscript to distinguish their initial and final values. This means

$V_1=V_2=V$ and $N_1=N_2=N$

Making these substitutions in the ideal gas law equation for each state, and putting all the constants on one side we get

$P_1V=Nk_BT_1\ \Rightarrow\ \ \frac{P_1}{T_1}=\frac{Nk_b}{V}$

$P_2V=Nk_BT_2\ \Rightarrow\ \ \frac{P_2}{T_2}=\frac{Nk_b}{V}$

Since the right-hand sides of the two equations are equal, the left-hand sides must also be equal

$\frac{P_1}{T_1}=\frac{P_2}{T_2}$

Before we put numbers in, we must convert all units to standard units for the ideal gas law.

$T_1=18.0 + 273.15 \ \Rightarrow\ \ T_1=291K$

$T_2=35.0 + 273.15 \ \Rightarrow\ \ T_2=308K$

Therefore

$\frac{7.00 \times 10^5 Pa}{291K}=\frac{P_2}{308K}$

$P_2=7.41 \times 10^5 Pa$

In the Ideal Gas Law, $PV=Nk_BT$ , P is the absolute pressure of the gas. But when we use a tool to measure, let’s say, tire pressure, we are measuring the pressure of the air inside the tire relative to the atmospheric pressure, and not its absolute pressure. We call this the gauge pressure. Pressure can be measured in various units. Some common units are pascal (Pa), atmosphere (atm), pound per square inch (psi), and millimeters of mercury (mmHg). The pressure applied by the column of air above us at sea level is 1atm=1.013×10⁵ Pa. The relationship between the absolute pressure, P, and the gauge pressure, P_gauge is:

$\boxed{P=P_{gauge} + 1 atm}$

Example 17.2 – Number Of Air Molecules In a Bicycle Tire

A bicycle tire has a volume of 1.35L and a gauge pressure of 60.0psi at 72.0°F. Find the number of air molecules in this tire.

Solution

We can use the Ideal Gas Law to solve for N, the number of molecules. But first, we have to put all the given parameters in the appropriate units.

Volume must be in m³.

$V=1.35L \times \frac{1 m^3}{1000L}$

$V=1.35\times 10^{-3} m^3$

Pressure has to be absolute pressure in Pascal.

$P_{gauge}=60.0 psi \times \frac{6894.76 Pa}{1psi}$

$P_{gauge}=4.14\times 10^{5} Pa$

$P=P_{gauge} + 1.013 \times 10^5 Pa$

$P=4.14\times 10^{5} Pa + 1.013 \times 10^5 Pa$

$P=5.15 \times 10^5 Pa$

The temperature has to be in Kelvin.

$T_F=\frac{9}{5}T_C+32$

$72.0=\frac{9}{5}T_C+32$

$T_C =\frac{5}{9}(72.0 - 32)$

$T_C =22.2^\circ C$

$T_K=T_C+273.15$

$T_K=22.2+273.15$

$T_K=295K$

Now we are ready to use the Ideal Gas Law

$PV=Nk_BT$

$(5.15 \times 10^5 Pa)(1.35\times 10^{-3} m^3)=N(1.38 \times 10^{-23}J/K)(295K)$

$N=1.71 \times 10^{23 }\ molecules$

Discussion

That is a HUGE number of molecules. It is 171,000,000,000,000,000,000,000 molecules!!! That’s roughly 20,000,000,000,000 times the population of Earth.

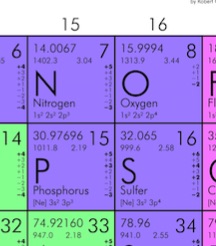
In the Ideal Gas Law equation, $PV=Nk_BT$ , N is the number of molecules in the gas. For any macroscopic sample of gas, the number of molecules is extremely large. Since doing calculations with very large numbers can be cumbersome, it is more convenient to group molecules into standard bundles, and keep track of the number of bundles instead of the number of molecules. The standard “bundle” to use in this context is called “mole”. One mole contains 6.02×10²³ molecules. The number of molecules in one mole is known as Avogadro’s number, N_A. In Example 16.3, the number of moles of air in the tire is $\frac{1.71 \times 10^{23 }}{6.02 \times 10^{23}}=0.284 mol$ . Furthermore, the mass of one mole of an element can be determined using the periodic table. Consider the following elements in the periodic table:

The number 4.002602 for Helium means that 1mol of He has a mass of 4.002602g. In other words, 6.02×10²³ atoms of He have a combined mass of 4.002602g. Since He is a monatomic gas, 1 mol of He gas has a mass of 4.002602g.

The number 15.9994 for Oxygen means that 1mol of O has a mass of 15.9994g. In other words, 6.02×10²³ atoms of O have a combined mass of 15.9994g. But since O is a diatomic gas, 1 mol of Oxygen gas is really 1 mol of O₂. Therefore, 1 mol of Oxygen gas has a mass of 2X(15.9994g)=31.9999g. In summary:

$N_A=6.02\times 10^{23}$ Avogadro’s Number

1 mol contains $6.02\times 10^{23}$ molecules.

The atomic mass of an element in “gram” Is the mass of 1 mol of the atoms of that element.

To express the Ideal Gas Law in terms of the number of moles instead of the number of molecules, we can divide and multiply the right-hand side by Avogadro’s Number.

$PV=Nk_BT$

$PV=\frac{N}{N_A} N_A k_B T$

Notice that $\frac{N}{N_A}$ is the number of moles. We represent the number of moles with n. Therefore $\frac{N}{N_A}=n$ . Also $N_A k_B$ is a constant. We call this constant the Universal Gas Constant, and we represent it with R.

$R=N_A k_B$

$R=(6.02 \times 10^{23} molecules/mol)(1.38 \times10^{-23}J/K)$

$R=8.31J/mol.K$

Putting it all together, we get this alternative equation for the Ideal Gas Law.

$\boxed{PV=nRT}$ Ideal Gas Law

In this equation,

$P$ is the absolute pressure ( $Pressure=\frac{force}{volume}$ ), and is measured in units of Pascal (Pa). Pa=N/m³

$V$ is the volume which is the amount of space the gas occupies and is measured in units of m³

$n$ is the number of moles of gas

$R$ is the Universal Gas Constant. $R= 8.31J/mol.K$

$T$ is the absolute temperature of the gas in Kelvin

kinetic theory

In this section, we relate the macroscopic quantities of pressure and temperature to the motion of molecules in a sample of gas.

The figure shows an expanded view of an elastic collision of a gas molecule with the wall of a container. Calculating the average force exerted by such molecules will lead us to the ideal gas law, and to the connection between temperature and molecular kinetic energy. We assume that a molecule is small compared with the separation of molecules in the gas and that its interaction with other molecules can be ignored. We also assume the wall is rigid and that the molecule’s direction changes, but that its speed remains constant (elastic collision).

If the molecule’s velocity changes in the x-direction, its momentum changes from -mv_xto +mv_x. Thus, its change in momentum is $\Delta P=+mv_x -(-mv_x)=2mv_x$ . Using Newton’s Second Law, The force exerted on the molecule is given by

$F=\frac{\Delta P}{\Delta t}=\frac{2mv_x}{\Delta t}$

There is no force between the wall and the molecule until the molecule hits the wall. During the short time of the collision, the force between the molecule and the wall is relatively large. We are looking for an average force; we take $\Delta t$ to be the average time between collisions of the molecule with this wall. It is the time it would take the molecule to go across the box and back, a distance $2l$ at a speed of $v_x$ Thus $\Delta t=\frac{2l}{v_x}$ and the expression for the force becomes

$F=\frac{2mv_x}{\frac{2l}{V_x}}=\frac{mv_x^2}{l}$

This force is due to one molecule. We multiply by the number of molecules, N, and use their average squared velocity to find the force

$F=N\frac{m\overline{v_x^2}}{l}$

where the bar over a quantity means its average value. We would like to have the force in terms of the speed, v, rather than the x-component of the velocity. We note that the total velocity squared is the sum of the squares of its components, so that

$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}$

Because the velocities are random, their average components in all directions are the same:

$\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}$

Thus,

$\overline{v^2}=3\overline{v_x^2}$

or

\overline{v_x^2}= \frac{1}{3}\overline{v^2}

Substituting $\frac{1}{3}\overline{v^2}$ into the expression for F gives

$F=N\frac{m\overline{v^2}}{3l}$

The pressure is force per area, $P=\frac{F}{A}$ , so that we obtain

$P=\frac{F}{A}=N\frac{m\overline{v^2}}{3Al}=\frac{1}{3} \frac{Nm\overline{v^2}}{V}$

where we used V=Al for the volume. This gives an important result.

$PV=\frac{1}{3}Nm\overline{v^2}$

This equation is another expression of the Ideal Gas Law. It also relates the macroscopic quantity of pressure to the motion of molecules.

Since the other form of the Ideal Gas Law is $PV=Nk_BT$ , we can set the right-hand sides equal to get

$\frac{1}{3}Nm\overline{v^2}=Nk_BT$

We can get the average kinetic energy of a molecule, $\frac{1}{2}mv^2$ , from the right-hand side of the equation by canceling N and multiplying by 3/2. This calculation produces the result that the average kinetic energy of a molecule is directly related to absolute temperature.

$\overline{KE}=\frac{1}{2}m\overline{v^2} = \frac{3}{2}k_B T$ Average Kinetic Energy Per Molecule

The equation above relates the macroscopic quantity of temperature to molecular motion. More specifically it shows that temperature is directly proportional to the average translational kinetic energy per molecule.

We can also rearrange the equation above to solve for, $\sqrt{\overline{v^2}}$ , root-mean-square (rms) speed, v_rms.

$\sqrt{\overline{v^2}}=v_{rms}=\sqrt{\frac{3k_B T}{m}}$

v_rms represents the average speed of molecules.

Section summary

What you need to take away from all these derivations in this section is that temperature is directly proportional to the average translational kinetic energy per molecule.

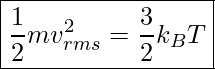$\boxed{\frac{1}{2}mv_{rms}^2 = \frac{3}{2}k_B T}$ Average Kinetic Energy Per Molecule & Absolute Temperature

In this equation

$m$ is the mass of one molecule in kg

$v_{rms}$ is the root-mean-square speed of a molecule in m/s. You can think of this as the average speed of a molecule.

$k_B$ is the Boltzmann Constant. $k_B= 1.38\times 10^{-23}J/K$

$T$ is the absolute temperature of the gas in Kelvin

Example 17.3 – Average Speed Of Air Molecules

Air is roughly 80% Nitrogen and 20% Oxygen. Find the average speed (v_rms) of N₂ molecules in a room at 20.0°C.

Solution for (a)

The average speed of molecules is related to the temperature of the gas according to

$\frac{1}{2}mv_{rms}^2 = \frac{3}{2}k_B T$

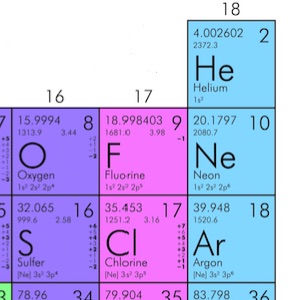
We need to find m, the mass of one molecule of N₂.

Let’s look up Nitrogen in the periodic table

calculating the mass of one molecule of N₂:

mass of 1mol of N atoms = 14.0067g

mass of 1 mol of N₂ molecules = 28.0134g

mass of 6.02×10²³ molecules of N₂ = 28.0134g

mass of 1 molecule of N₂ = $\frac{28.0134g}{6.02 \times 10^{23}}=4.65 \times 10^{-23} g$

Mass must be in kg.

$4.65 \times 10^{-23} g \times \frac{1kg}{1000g}=4.65 \times 10^{-26}kg$

The temperature must be in Kelvin.

$T_K=T_C+273.15$

$T_K=20.0+273.15$

$T_K=293K$

Now we are ready to calculate v_rms for Nitrogen

$\frac{1}{2}mv_{rms}^2 = \frac{3}{2}k_B T$

$\frac{1}{2}(4.65 \times 10^{-26}kg) v_{rms}^2 = \frac{3}{2}(1.38\times 10^{-23}J/K)(293K)$

$v_{rms} =511m/s$

Attributions

This chapter contains material taken from Openstax College Physics-Temperature, Kinetic Energy, and the Gas Laws, and Openstax University Physics Volume 2, and is used under a CC BY 4.0 license. Download these books for free at Openstax

Information in the Human Body Temperature section is obtained from a Wikipedia entry on Thermoregulation.

To see what was changed, refer to the List of Changes.

questions and Problems

Questions

[openstax college phys. quest13.11] Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?
[openstax college phys. quest13.10] Is there a mole of people inhabiting Earth?
[openstax univ. phys. vol2. quest2.17 modifed] An ideal gas is at a temperature of 27°C. To double the average speed of its molecules, what does the temperature need to be changed to?
[openstax univ. phys. vol2. quest2.15 modifed] One cylinder contains helium gas and another identical cylinder contains krypton gas at the same temperature. Mark each of these statements true, false, or impossible to determine from the information given. Justify all your answers.
1. The average speeds (v_rms) of atoms in the two gases are the same.
2. The average kinetic energies of atoms in the two gases are the same.
3. The pressures in the two gases are the same.

problems

[openstax univ. phys. vol. 2 – 2.18] The gauge pressure in your car tires is 2.50×10⁵Pa at a temperature of35.0ºC when you drive it onto a ship in Los Angeles to be sent to Alaska. What is their gauge pressure on a night in Alaska when their temperature has dropped to -40.0ºC? Assume the tires have not gained or lost any air.
[openstax univ. phys. vol. 2 – 2.19] Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of 20.0ºC. Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is 60.0ºC (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks.
A balloon filled with air has a volume of 0.200m³ and a pressure of 20.0psi at a temperature of 92.0°F.
1. What is the new volume if the balloon is placed in a refrigerator and cooled to 32.0°F and the pressure is reduced to 14.7psi?
2. How many moles of air are there in the balloon?
[openstax univ. phys. vol. 2 – 2.24] An airplane passenger has 100cm³ of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to 7.50×104 Pa?
[openstax univ. phys. vol. 2 – 2.27] An expensive vacuum system can achieve a pressure as low as 1.00×10^-7Pa at 20.0ºC How many molecules are there in a cubic centimeter at this pressure and temperature?
[openstax univ. phys. vol. 2 – 2.34] A car tire at a temperature of 25.0ºC contains 3.60 mol of gas in a 30.0-L volume.
1. What is the gauge pressure of air in this tire?
2. What will the gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and 25.0ºC? Assume the temperature remains at25.0ºC and the volume remains constant.
[openstax univ. phys. vol. 2 – 2.38] Some incandescent light bulbs are filled with argon gas. What is the v_rms for argon atoms near the filament, assuming their temperature is 2500 K?
[openstax univ. phys. vol. 2 – 2.42] What is the total translational kinetic energy of the air molecules in a room of volume 23.0m³ if the pressure is 9.50×10⁴Pa, and the temperature is 21.0ºC?
A nitrogen canister has a volume of 5.00L and contains gas at a pressure of 2200psi at 20.0°C.
1. Find the mass of nitrogen gas in the container.
2. What is the average kinetic energy per molecule?
3. What is the v_rms of the nitrogen molecules in this container?
Determine the density of CO₂ at a temperature of 75.0°F and a pressure of 0.950atm.
What is the molar mass of a gas if 0.0494 g of the gas occupies a volume of 0.100 L at a temperature 26 °C and a pressure of 5.94 psi?
A 2.00L cylinder contains laughing gas, N₂O, at a temperature of 30.0ºC and at atmospheric pressure
1. What is the mass of the gas in this container?
2. What is the v_rms of the N₂O molecules?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

ideal gas law

kinetic theory

Section summary

Attributions

questions and Problems

Questions

problems

License

Share This Book