UNIT 17 – Methods of Heat Transfer and Calorimetry

Beta Keramati

Temperature and Heat Transfer

Last Update: 7/1/2024

heat – flow of thermal energy

In UNIT 16 we saw that the absolute temperature of an ideal gas is a measure of average translational kinetic energy per molecule. In a more general sense that is also applicable to solids and liquids, temperature is a measure of average kinetic energy that is associated with the random motions of atoms and molecules. The overall energy associated with the random motions of atoms and molecules in a substance is called Thermal energy. The molecules of two objects that are at different temperatures have, on average, different amounts of kinetic energy. If two objects that are at different temperatures are brought in contact with each other, thermal energy is transferred from the hotter to the colder object until equilibrium is reached and the bodies reach thermal equilibrium (i.e., they are at the same temperature). The transfer of energy is caused by the temperature difference and ceases once the temperatures are equal. These observations lead to the following definition of heat: Heat is the flow of thermal energy.

Since heat is the transfer of thermal energy, heat is measured in units of joules. Another common unit for heat is calories. One calorie(cal) is the energy needed to raise the temperature of one gram of water by one degree Celsius. One food calorie (Cal) is one kcal and 1cal=4.186J. In this text, heat is represented with Q. If thermal energy is transferred into a substance Q>0, and if it is transferred out of a substance Q<0.

Methods of transfer of thermal energy

Conduction is heat transfer through stationary matter by physical contact. For example, heat transferred between the electric burner of a stove and the bottom of a pan is transferred by conduction.
Convection is the heat transfer by the macroscopic movement of a fluid. For example, this type of transfer takes place in a forced-air furnace and in weather systems.
Heat transfer by radiation occurs when microwaves, infrared radiation, visible light, or another form of electromagnetic radiation is emitted or absorbed. An example is the warming of the Earth by the Sun. A less obvious example is thermal radiation from the human body.

Figure 17.1 shows how heat is transferred through all three methods from a fireplace.

Let’s consider each method of heat transfer in more detail.

Conduction

You might have noticed that as you walk barefoot on a carpet in a cold house and then step onto the tile floor in another room your feet feel cold. This result is intriguing since the carpet and tile floor are both at the same temperature. The different sensation you feel is explained by the different rates of heat transfer: the heat loss during the same time interval is greater for skin in contact with the tiles than with the carpet, so the temperature drop is greater on the tiles.

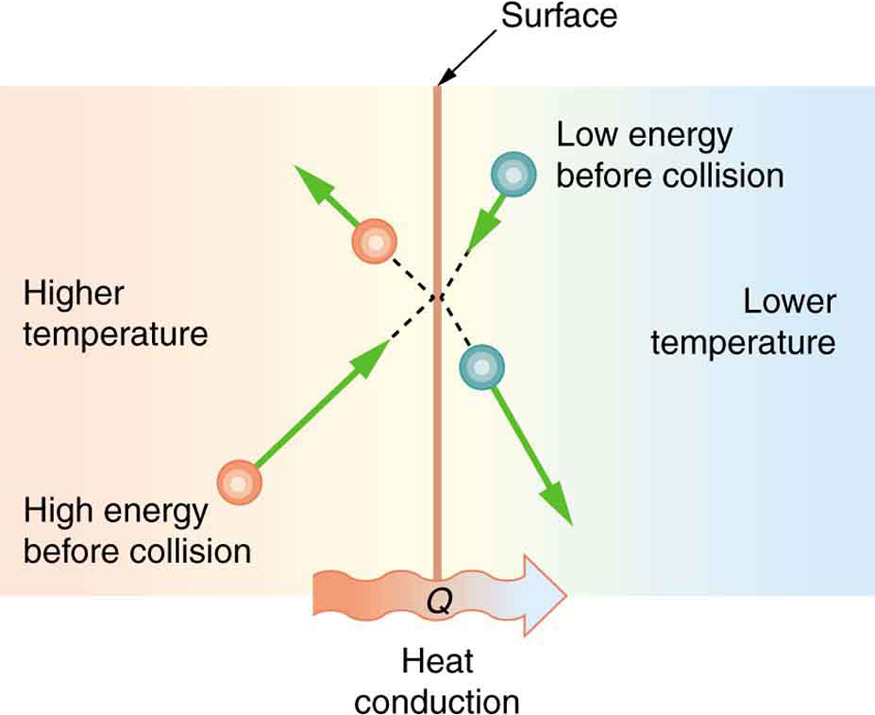
Some materials conduct thermal energy faster than others. In general, good conductors of electricity (metals like copper, aluminum, gold, and silver) are also good heat conductors, whereas insulators of electricity (wood, plastic, and rubber) are poor heat conductors. Figure 17.2 shows molecules in two bodies at different temperatures. The (average) kinetic energy of a molecule in the hot body is higher than in the colder body. If two molecules collide, an energy transfer from the molecule with greater kinetic energy to the molecule with less kinetic energy occurs. The cumulative effect from all collisions results in a net flux of heat from the hot body to the colder body. The heat flux thus depends on the temperature difference ΔT=T_hot-T_cold. Therefore, you will get a more severe burn from boiling water than from hot tap water. Conversely, if the temperatures are the same, the net heat transfer rate falls to zero, and equilibrium is achieved. Since the number of collisions increases with the increasing area, heat conduction depends on the cross-sectional area. If you touch a cold wall with your palm, your hand cools faster than if you just touch it with your fingertip.

A third factor in the mechanism of conduction is the thickness of the material through which heat transfers. Figure 17.3 shows a slab of material with different temperatures on either side. Suppose that T₂ is greater than T₁ so that heat is transferred from left to right. Heat transfer from the left side to the right side is accomplished by a series of molecular collisions. The thicker the material, the more time it takes to transfer the same amount of heat. This model explains why thick clothing is warmer than thin clothing in winter, and why Arctic mammals protect themselves with thick blubber.

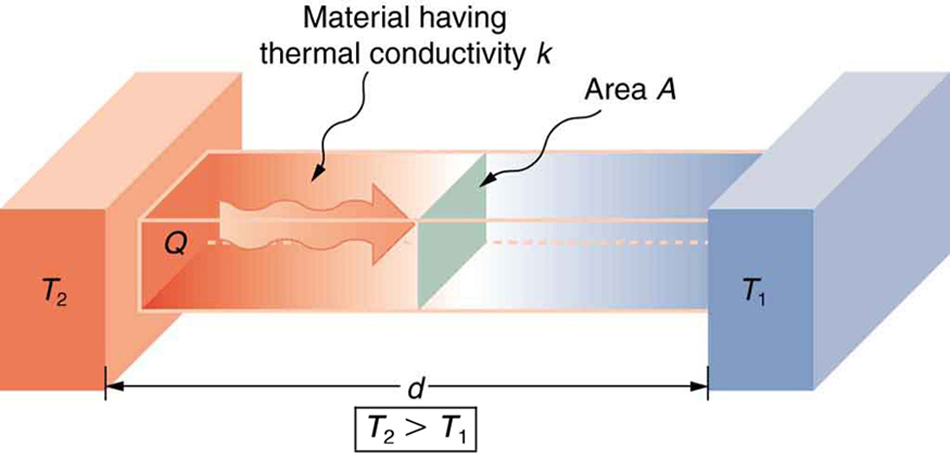
Lastly, the heat transfer rate depends on the material properties described by the coefficient of thermal conductivity. All four factors are included in a simple equation that was deduced from and confirmed by experiments. The rate of conductive heat transfer through a slab of material, such as the one in Figure 17.3, is given by

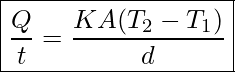$\boxed{\frac{Q}{t}=\frac{KA(T_2-T_1)}{d}}$ Rate of Heat Transfer Through Conduction

In this equation $\frac{Q}{T}$ is the rate of heat transfer in watts (watt=J/s), K is the thermal conductivity of the material, A and d are its surface area and thickness respectively, as shown in Figure 17.3, and T₂-T₁ is the temperature difference across the slab.

Table 17.1 gives representative values of thermal conductivity.

Example 17.1

Water is boiling in an aluminum pan placed on an electrical element on a stovetop. The saucepan has a circular bottom that is 0.800 cm thick and 14.0 cm in diameter. Heat is transferred to the water at a rate of 2256 watts. What is the temperature difference across (through) the bottom of the pan?

Solution

The rate of heat transfer through conduction is given by

$\frac{Q}{t}=\frac{KA(T_2-T_1)}{d}$

From Table 17.1 we see that the thermal conductivity of aluminum is K=220J/s.m.°C

The area of the bottom of the pan is

$A=\pi r^2$

$A=\pi (\frac{0.140m}{2})^2$

$A=0.0154m^2$

And the thickness of the pan is d=0.800cm or d=0.00800m.

Putting it all together we get

$\frac{Q}{t}=\frac{KA(T_2-T_1)}{d}$

$2256 watt=\frac{(220J/s.m.^\circ C)(0.0154m^2)(T_2-T_1)}{0.00800m}$

$(T_2-T_1)=5.33^\circ C$

Discussion

Conduction is caused by the random motion of atoms and molecules. As such, it is an ineffective mechanism for heat transport over macroscopic distances. Take, for example, the temperature on the Earth, which would be unbearably cold during the night and extremely hot during the day if heat transport in the atmosphere were to be only through conduction. In another example, car engines would overheat unless there was a more efficient way to remove excess heat from the pistons.

Convection

Convection is driven by the large-scale flow of matter. In the case of Earth, the atmospheric circulation is caused by the flow of hot air from the tropics to the poles, and the flow of cold air from the poles toward the tropics. (Note that Earth’s rotation causes the observed easterly flow of air in the northern hemisphere). Car engines are kept cool by the flow of water in the cooling system, with the water pump maintaining a flow of cool water to the pistons. The circulatory system in the body keeps the body cool in a similar way. When the body overheats, the blood vessels in the skin expand (dilate), which increases the blood flow to the skin which can be cooled by sweating. These vessels become smaller when it is cold outside and larger when it is hot (so more fluid flows and more energy is transferred). The body also loses a significant fraction of its heat through the breathing process.

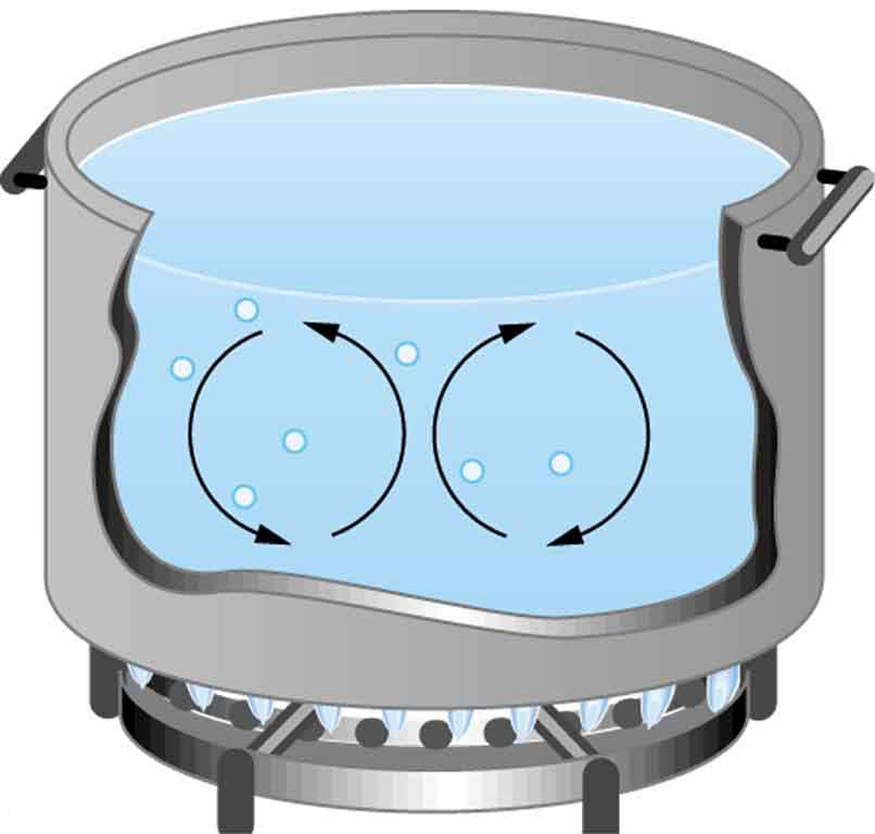
Natural convection is driven by buoyant forces: hot air rises because density decreases as temperature increases. The pot of water on the stove in Figure 17.4 is heated in the same manner. The hotter water expands, it decreases in density and rises to transfer heat to other regions of the water, while colder water sinks to the bottom. Similarly, ocean currents and large-scale atmospheric circulation transfer energy from one part of the globe to another and are examples of natural convection.

Forced convection is a common method of heat transfer used in central heating and air conditioning systems. A ceiling fan also promotes heat transfer through forced convection.

Radiation

You can feel the heat transfer from fire and the Sun. Similarly, you can sometimes tell that the oven is hot without touching its door or looking inside—it may just warm you as you walk by. The space between the Earth and the Sun is largely empty, without any possibility of heat transfer by convection or conduction. In these examples, heat is transferred by radiation. That is, the hot body emits electromagnetic waves that are absorbed by our skin: no medium is required for electromagnetic waves to propagate. Different names are used for electromagnetic waves of different wavelengths: radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.

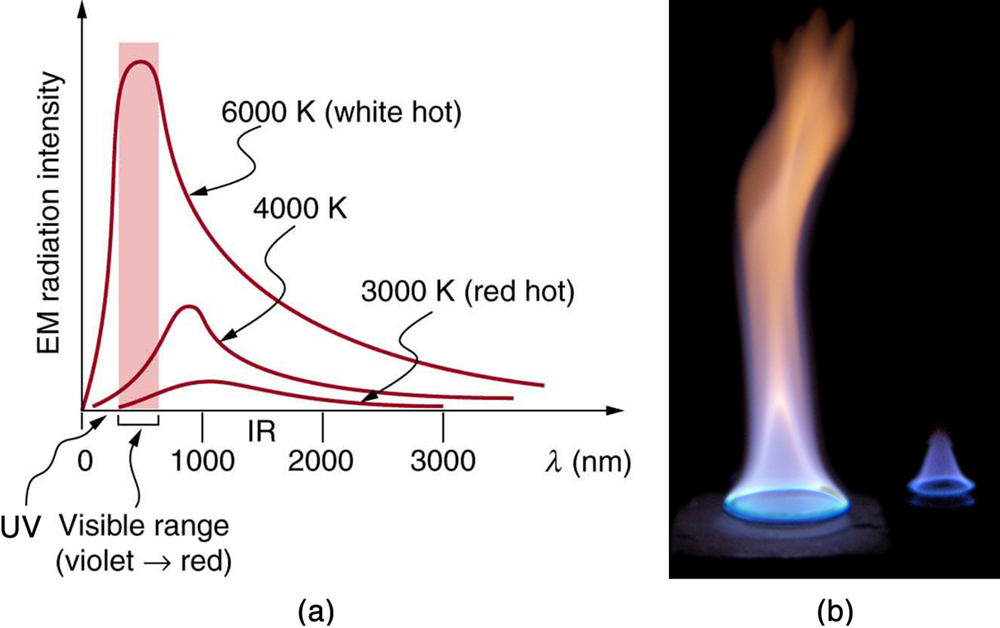
The energy of electromagnetic radiation varies over a wide range, depending on the wavelength: A shorter wavelength (or higher frequency) corresponds to higher energy. Because more heat is radiated at higher temperatures, higher temperatures produce more intensity at every wavelength but especially at shorter wavelengths. In visible light, wavelength determines color—red has the longest wavelength and violet the shortest—so a temperature change is accompanied by a color change. For example, an electric heating element on a stove glows from red to orange, while the higher-temperature steel in a blast furnace glows from yellow to white. Infrared radiation is the predominant form radiated by objects cooler than the electric element and the steel. The radiated energy as a function of wavelength depends on its intensity, which is represented in Figure 17.5(a) by the height of the distribution.

(c)

Figure 17.5

The intensity or rate of radiation emission increases dramatically with temperature and the spectrum shifts toward the visible and ultraviolet (lower wavelength). In Figure 17.5(a) the shaded portion denotes the visible part of the spectrum. It is apparent that the shift toward the ultraviolet with temperature makes the visible appearance shift from red to white to blue as temperature increases. Note the variations in the color corresponding to variations in flame temperature in Figure 17.5(b).

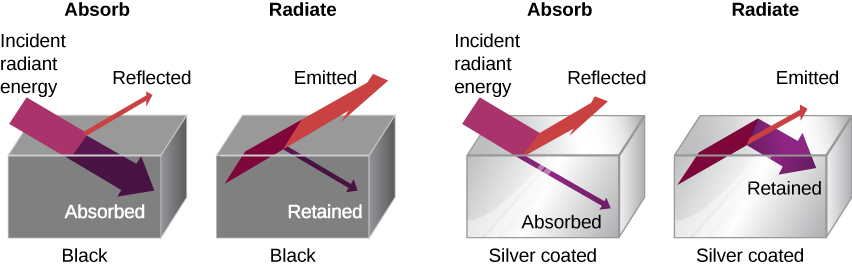
The rate of heat transfer by radiation also depends on the object’s color. Black is the most effective, and white is the least effective. On a clear summer day, black asphalt in a parking lot is hotter than the adjacent gray sidewalk, because black absorbs better than gray. The reverse is also true—black radiates better than gray. Thus, on a clear summer night, the asphalt is colder than the gray sidewalk, because black radiates the energy more rapidly than gray. A perfectly black object would be an ideal radiator and an ideal absorber, as it would capture all the radiation that falls on it. In contrast, a perfectly white object or a perfect mirror would reflect all radiation and a perfectly transparent object would transmit it all. Such objects would not emit any radiation. This is shown in Figure 17.5(c). Mathematically, the color is represented by the emissivity e. A “blackbody” radiator would have an e=1, whereas a perfect reflector or transmitter would have e=0. For real examples, tungsten light bulb filaments have an e of about 0.5, and carbon black (a material used in printer toner) has an emissivity of about 0.95.

The rate of heat transfer by emitted radiation is determined by the Stefan-Boltzmann law of radiation:

$\boxed{\frac{Q}{t}=\sigma eAT^4}$

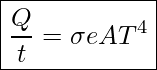
Rate of Heat Transfer Through Radiation

In this equation $\sigma$ is the Stefan-Boltzmann constant, and $\sigma= 5.67 \times 10^{-8} J/s.m^2.K^4$
$e$ is the emissivity of the object
$A$ is the surface area of the object in m²
$T$ is the absolute temperature in Kelvin

The radiation rate is directly proportional to the fourth power of the absolute temperature—a remarkably strong temperature dependence. Furthermore, the radiated heat is proportional to the surface area of the object. If you knock apart the coals of a fire, there is a noticeable increase in radiation due to an increase in radiating surface area.

Skin is a remarkably good absorber and emitter of infrared radiation, having an emissivity of 0.97 in the infrared spectrum. This high infrared emissivity is why we can so easily feel radiation on our skin. It is also the basis for the use of night scopes used by law enforcement and the military to detect human beings. Even small temperature variations can be detected because of the T⁴ dependence. Images, called thermographs, can be used medically to detect regions of abnormally high temperature in the body, perhaps indicative of disease. Similar techniques can be used to detect heat leaks in homes, optimize the performance of blast furnaces, improve comfort levels in work environments, and even remotely map the Earth’s temperature profile. Figure 17.6 is a thermograph of part of a building and shows temperature variations, indicating where heat transfer to the outside is most severe. Windows are a major region of heat transfer to the outside of homes.

All objects emit and absorb radiation. The net rate of heat transfer by radiation (absorption minus emission) is related to both the temperature of the object and the temperature of its surroundings. Assuming that an object with a temperature T₁ is surrounded by an environment with a uniform temperature T₂, the net rate of heat transfer by radiation is

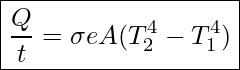$\boxed{\frac{Q}{t}=\sigma eA(T_2^4- T_1^4)}$ Net Rate of Heat Transfer Through Radiation

Example 17.2

What is the change in the rate of the radiated heat by a body at the temperature of T₁=20.0°C compared to when the body is at the temperature T₂=40.0°C?

Solution

To compare the rate of heat transfer through radiation at the two temperatures we can calculate the ratio of the two.

$\frac{(\frac{Q}{t})_2}{(\frac{Q}{t})_1} = \frac {\sigma eAT_2^4}{\sigma eAT_1^4}$

$\frac{(\frac{Q}{t})_2}{(\frac{Q}{t})_1} = \frac {T_2^4}{T_1^4}$

Temperatures must be in Kelvin.

$T_K=T_C+273.15$

$T_K=20.0+273.15$

$T_1=293K$

$T_K=40.0+273.15$

$T_2=313K$

Therefore

$\frac{(\frac{Q}{t})_2}{(\frac{Q}{t})_1} = \frac {(313K)^4}{(293K)^4}$

$\frac{(\frac{Q}{t})_2}{(\frac{Q}{t})_1} = 1.30$

This means that the rate of energy transfer through radiation increases by 30%.

Example 17.3

Human skin has an emissivity of approximately 0.98. Without any clothing, what is the net rate of energy loss due to radiation from the body of a person whose surface area is 1.8m² in a room kept at 65.0°F?

Solution

The average human body temperature is 98.6°F. To determine the net rate of heat transfer through radiation, we must first convert the body temperature and the temperature of the environment to Kelvin.

$T_F=\frac{9}{5}T_C+32$

$98.6=\frac{9}{5}T_{1C}+32$

$T_{1C} =\frac{5}{9}(98.6 - 32)$ $T_{1C} =37.0^\circ C$

$T_K=T_C+273.15$

$T_1=37.0+273.15$

$T_1=310K$

$65.0=\frac{9}{5}T_{1C}+32$

$T_{2C} =\frac{5}{9}(65.0 - 32)$ $T_{2C} =18.3^\circ C$

$T_2=18.3+273.15$

$T_2=291K$

The net rate of energy loss through radiation is

$\frac{Q}{t}=\sigma eA(T_2^4- T_1^4)$

$\frac{Q}{t}=(5.67 \times 10^{-8} J/s.m^2.K^4)(0.98)(1.8m^2)((291K)^4- (310K)^4)$

$\frac{Q}{t}=-210 watts$

Notice that a negative rate of heat transfer means the body is releasing heat.

Burning Calories and Weight Loss

We often talk about “burning” calories to lose weight, but what does that really mean scientifically? First, what we really mean is lose mass because that is the measure of how much stuff is in our bodies and weight depends on where you are (it’s different on the moon). Second, our bodies can’t just interchange mass and energy. So how do we actually lose mass by exercising? We don’t actually shed the atoms and molecules that make up body tissues like fat by “burning” them. Instead, we break down the fat molecules into smaller molecules and then break bonds within those molecules to release chemical potential energy, which we eventually convert to work and exhaust heat. The atoms and smaller molecules that result from breaking the bonds combine to form carbon dioxide and water vapor (CO₂ and H₂O) and we breathe them out. We also excrete H₂O in sweat and urine. The process is similar to burning wood in a campfire — in the end, you have much less mass of ash than you did the original wood. Where did the rest of the mass go? Into the air as CO₂ and H₂O. The same is true for the fuel burned by your car. For more on this concept see the video below. The really amazing fact is that your body completes this chemical process without the excessive temperatures associated with burning wood or fuel, which would damage your tissues. The body’s trick is to use enzymes, which are highly specialized molecules that act as catalysts to improve the speed and efficiency of chemical reactions.

calorimetry- Temperature change and Phase change

The process of measuring heat transferred to or from a substance is called calorimetry. In this section, we discuss the effect of heat transfer on solids and liquids. In general, when heat is transferred to or from a solid or liquid two things can happen but never at the same time: the substance undergoes a change in temperature, or the substance experiences a change in phase.

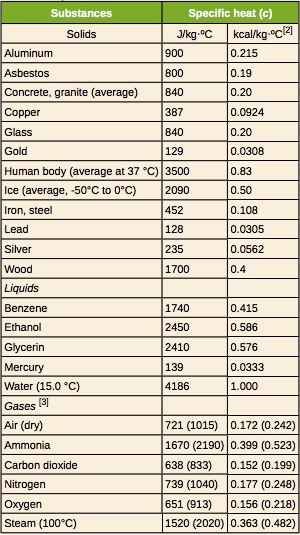
Let’s consider temperature change first. The amount by which the temperature of a substance changes when heat is transferred to or from that substance depends on a property called specific heat capacity, c. Specific heat capacity is defined as the amount of heat needed to change the temperature of 1kg of a substance by 1°C. For example, the specific heat of water is 4186J/kg.°C. This means that 4186J of thermal energy must be added to or removed from 1kg of water to change its temperature by 1°C. Based on this definition, it is easy to see that to change the temperature of 2kg of water by 1°C, 2x(4186J) of heat is necessary. Similarly, we would need 3x2x(4186J) of heat to change the temperature of 2kg of water by 3°C. Representing this reasoning in the form of an equation, we get

$\boxed{Q=mc\Delta T}$ Heat Needed To Cause Change In Temperature

where
$Q$ is heat transferred to or from the substance in units of Joule
$m$ is the mass of the substance in kg
$c$ is the specific heat capacity of the substance in J/kg.°C
$\Delta T$ is the change in temperature of the substance.

Notice that the sign for $Q$ is embedded in the sign for $\Delta T$ . When thermal energy is transferred to a substance and heat flows into it $Q>0$ , and so is its change in temperature $\Delta T>0$ . Similarly, if thermal energy is removed from a substance and heat flows out of it $Q<0$ and $\Delta T<0$ .

When heat transfer causes temperature change, it means that the energy added to (or removed from) the substance alters the average kinetic energy due to the random motion of atoms or molecules of that substance.

The specific heat of a substance is determined experimentally. Table 17.2 provides the specific heat capacity of some common substances.

Example 17.4

A 0.500 kg aluminum pan on a stove is used to heat 0.250 liters of water from 20.0°C to 80.0°C

a) How much heat is required?

b)What percentage of the heat is used to raise the temperature of the water?

Solution for (a)

The overall heat needed must increase the temperature of the aluminum pan and water from 20.0°C to 80.0°C.

$Q=m_{Al}c_{Al}(\Delta T)_{Al} +m_{w}c_{w}(\Delta T)_{w}$

We look up the specific heat of aluminum and water in Table 17.2.

We need to determine the mass of 0.250L of water. The density of water is 1000kg/m³, and 1000L=1m³. Therefore

$1000 \frac{kg}{m^3}=\frac{m}{0.250L} \times \frac{1000L}{1m^3}$

$m=0.250kg$

Now we can calculate the total heat that flows into the aluminum and water.

$Q=(0.500kg)(900J/kg.^\circ C)(80.0^\circ C - 20.0^\circ C)+(0.250kg)(4186J/kg.^\circ C)(80.0^\circ C-20.0^\circ C)$

$Q=89800J=8.98kJ$

Solution for (b)

The amount of heat that flows into water is

$Q_w=(0.250kg)(4186J/kg.^\circ C)(80.0^\circ C - 20.0^\circ C)$

$Q_w=62800J=6.28kJ$

Therefore the percentage of heat that flows into the water is

$\frac{62800J}{89800J} \times 100 \%=69.9 \%$

When two substances that are at different temperatures come in thermal contact with one another, they exchange heat until, eventually, they reach an equilibrium temperature. In this process, heat is transferred from the substance that is at a higher temperature to the substance that is at a lower temperature. If this system is well insulated, the heat transfer takes place only between the two substances. Since Q>0 when heat flows in, and Q<0 when heat flows out, the total sum of heat exchanged between the two substances must be zero. This means

$\sum Q=0$

This equation is valid for any number of substances that come in thermal contact with one another in an isolated system.

Example 17.5 – Equilibrium Temperature Of A Mixture

Suppose you pour 0.250 kg of 20.0°C water (about a cup) into a 0.500-kg aluminum pan off the stove at a temperature of 150°C. Assume that the pan is placed on an insulated pad and that a negligible amount of water boils off. What is the temperature when the water and pan reach thermal equilibrium a short time later?

Solution

Since the system is insulated, energy is conserved, and all the heat that flows out of the hot aluminum pan flows into the cool water. In other words

$\sum Q=0$

$Q_{Al} + Q_w=0$

The final temperature is the equilibrium temperature, T_eq, and is the same for both aluminum pan and water.

$m_{Al}c_{Al}(\Delta T)_{Al} + m_{w}c_{w}(\Delta T)_{w} =0$

$(0.500kg)(900J/kg.^\circ C)( T_{eq}-150^\circ C) + (0.250kg)(4186J/kg.^\circ C)( T_{eq}-20.0^\circ C) = 0$

$(450.0J/^\circ C) T_{eq}-6.750 \times 10^4 J + (1.0465 \times 10^3J/^\circ C) T_{eq}-2.093 \times 10^4 J =0$

$(1.496 \times 10^3J/^\circ C) T_{eq}-8.843 \times 10^4 J =0$

$T_{eq}=59.1^\circ C$

Discussion

This is a typical calorimetry problem—two bodies at different temperatures are brought in contact with each other and exchange heat until a common temperature is reached. Why is the final temperature so much closer to 20.0°C than 150°C? The reason is that water has a greater specific heat than most common substances and thus undergoes a small temperature change for a given heat transfer. A large body of water, such as a lake, requires a large amount of heat to increase its temperature appreciably. This explains why the temperature of a lake stays relatively constant during the day even when the temperature change of the air is large. However, the water temperature does change over longer times (e.g., summer to winter).

So far we have discussed heat transfer that results in temperature change. But sometimes heat flows into or out of a substance without any change in its temperature. This happens when the substance undergoes a phase change. Examples of phase change are transitions from solid to liquid, liquid to gas, solid to gas, and vice versa. To understand why there is no change in temperature during a phase change, let’s consider phase change from solid to liquid, such as the melting of a piece of ice. As shown in Figure 17.7, in a solid, there is a strong binding force between the molecules so that the molecules are more or less fixed in place. In a liquid, on the other hand, molecules move around more freely.

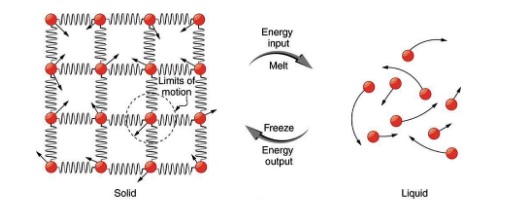
To convert a solid to liquid (for example ice into water) energy is needed to break the bonds between the molecules. Therefore, the whole time that the solid is melting, all the heat that flows into the solid goes into breaking the molecular bonds instead of increasing the kinetic energy of molecules. Therefore, during this phase change, heat flows into the substance, but the temperature does not change. The temperature at which a solid transitions into a liquid is called the melting point, or the melting temperature of the substance. The opposite happens and energy is released when a liquid freezes and turns into a solid. The temperature at which a solid melts is the same as the temperature at which that liquid freezes. In other words, the freezing temperature is equal to the melting temperature for any given substance.

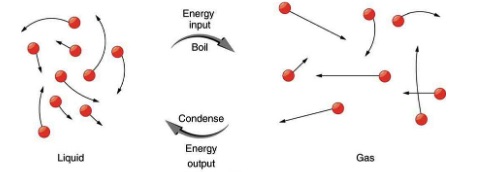
A similar argument applies to the phase change between liquid and gas as shown in Figure 17.8. Notice that the boiling temperature is equal to the condensation temperature for any given substance.

Latent heat is the energy required per kilogram to cause a phase change. The latent heat of fusion is the heat needed to melt 1kg of a solid. This is also the same amount of heat that flows out when 1kg of the same substance freezes. Similarly, latent heat of vaporization is the heat needed to cause phase change for 1kg of a substance from liquid to gas or from gas to liquid.

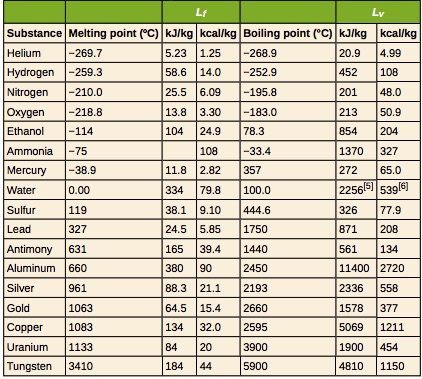
For example, the latent heat of fusion of ice is 3.34X10⁵J/kg. This means 3.34X10⁵J of heat is needed to melt 1kg of ice at 0°C. Also, if 1kg of water at 0°C freezes, 3.34X10⁵J of heat is released. Now, what if we wanted to determine the amount of heat needed to melt 2kg of ice at 0°C? It is easy to see that the answer is 2(3.34X10⁵J). We can generalize this in the following equation.

$\boxed{Q=mL}$ Heat Needed To Cause Phase Change

where

$m$ is the mass of the substance in kg

$L$ is the latent heat of the substance in J/kg

As always, when heat flows into a substance Q>0, and when heat flows out of a substance Q<0. When we use $Q=mL$ in our calculations, we must use the correct sign for Q depending on the situation.

Table 17.3 provides the freezing and melting temperatures along with latent heat of fusion and vaporization for some common substances.

Example 17.6 – Cooling Soda With Ice Cubes

Three ice cubes are used to chill a soda at 20°C with mass m_soda=0.25kg. The ice is at 0°C and each ice cube has a mass of 6.0 g. Assume that the soda is kept in a foam container so that heat loss can be ignored. Assume the soda has the same heat capacity as water. Find the final temperature when all the ice has melted.

Solution

Since the system of soda and ice cube is insulated, we can use conservation of energy for this process. This means that all the heat that flows out of the warmer soda flows into the cooler ice until the mixture reaches an equilibrium temperature.

Since ice is at its melting point (0°C), any heat that flows in is going to cause a phase change. If there is enough heat for ice to absorb it will melt completely first, and if there is any additional heat flowing in, the melted ice, which is now liquid water, will go through a temperature change.

Let’s find out how much heat is needed to melt all the ice.

$Q=mL$

$Q=(0.018kg)(3.34 \times 10^5J/kg$

$Q=6.012 \times 10^3 J$

This heat must come from warm soda. As heat flows out of the soda, it cools, but its temperature cannot go down indefinitely. If the temperature of soda reaches 0°C, it will freeze. So let’s see how much heat can flow out of the soda to reach 0°C.

$Q=(0.25kg)(4186J/kg.\circ C)(0^\circ C - 20^\circ C)$

$Q=-2.093 \times 10^4 J$

Since the maximum amount of heat that can be given off by soda to reach the freezing point is more than what ice needs to melt completely, we can conclude that all the ice will melt, and the resulting water absorbs enough heat from the soda until the whole mixture reaches an equilibrium temperature. Now that we know exactly what events are going to take place when heat transfer occurs between the hot and cold substances, we know what terms to include in the equation for conservation of energy.

$\sum Q=0$

$+\underbrace{m_{ice} L_f}_{melting\ of\ ice}+\underbrace{m_{ice}c_w(\Delta T)_w}_{warming\ of\ water}+ \underbrace{m_{soda} c_{soda}(\Delta T)_{soda}}_{cooling\ of\ soda}=0$

Notice that $\underbrace{m_{ice} L_f}_{melting\ of\ ice}$ is positive because heat is gained by ice as it melts.

$+(0.018kg)(3.34 \times 10^5J/kg)+(0.018kg)(4186J/kg.^\circ C)(T_{eq}-0^\circ C)+(0.25kg)(4186J/kg.^\circ C)(T_{eq}-20^\circ C)=0$

$6.012 \times 10^3 J + (75.348J/^\circ C)T_{eq} + (1.0465 \times 10^3J/^\circ C)T_{eq}-2.093 \times 10^4 J/^\circ C)=0$

$T_{eq}=13^\circ C$

Discussion

This example illustrates the enormous energies involved during a phase change. The mass of ice is about 7 percent of the mass of water but leads to a noticeable change in the temperature of soda.

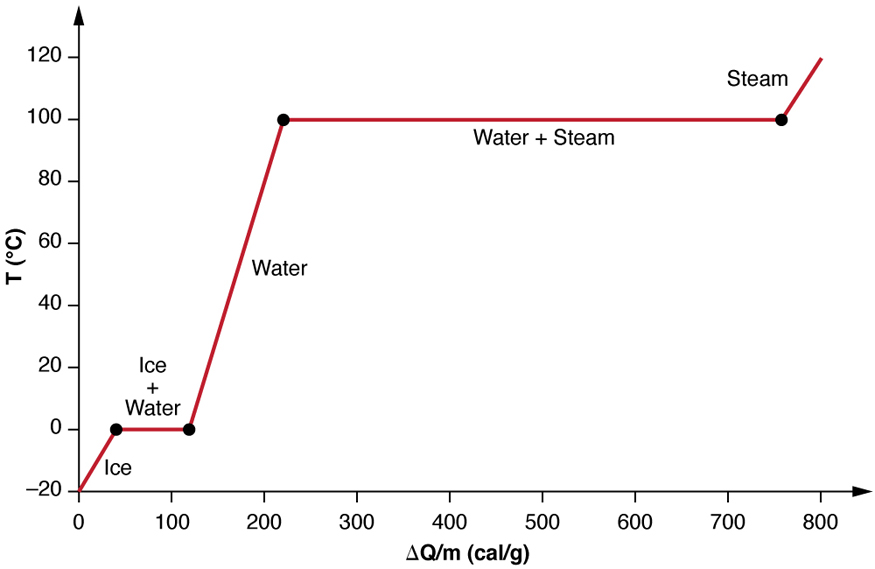
We examine the effects of phase change more precisely by considering heat flow into a sample of ice at -20°C (Figure 17.9). The temperature of the ice rises linearly, absorbing heat at a constant rate of 0.50 cal/g°C (2090J/kg°C) until it reaches 0°C. Once at this temperature, the ice begins to melt until all the ice has melted, absorbing 79.8 cal/g of energy. The temperature remains constant at 0°C during this phase change. Once all the ice has melted, the temperature of the liquid water rises, absorbing energy at a new constant rate of 1.00cal/g°C (4186J/kg°C). At 100°C, the water begins to boil and the temperature again remains constant while the water absorbs 539 cal/g of energy during this phase change. When all the liquid has become steam vapor, the temperature rises again, absorbing energy at a rate of 0.482 cal/g.°C.

Water can evaporate at temperatures below the boiling point. More energy is required than at the boiling point because the kinetic energy of water molecules at temperatures below 100°C is less than that at 100°C, hence less energy is available from random thermal motions. Take, for example, the fact that, at body temperature, perspiration from the skin requires a heat input of 2428 kJ/kg to evaporate. This is about 10 percent higher than the latent heat of vaporization at 100°C. This heat comes from the skin and thus provides an effective cooling mechanism in hot weather. High humidity inhibits evaporation, so that body temperature might rise, leaving un-evaporated sweat on your brow.

Just like vaporization is a cooling process, condensation is a warming process. When water vapor condenses, energy is released causing the surface over which condensation forms to warm. The glass in Figure 17.10 warms as water vapor condenses on its surface.

Attribution

This chapter contains material taken from Openstax College Physics-Heat and Heat Transfer Methods and is used under a CC BY 4.0 license. Download this book for free at Openstax

The section on radiation is taken from Openstax University Physics-Volume 2 – Mechanisms of Heat Transfer and is used under a CC BY 4.0 license. Download this book for free at Openstax

To see what was changed, refer to the List of Changes.

The section on Burning Calories and Weight Loss is taken from Body Physics: Motion to Metabolism, by Lawrence Davis and it is licensed under a CC BY NC SA 4.0 International License.

questions and problems

questions

How is heat transfer related to temperature?
Is it correct to say that if an object absorbs heat, its temperature will always increase? Justify your answer.
[openstax univ. phys. vol2. quest14.9] If you place 0°C ice into 0°C water in an insulated container, what will happen? Justify your answer.
[openstax college phys. quest13.14] A pressure cooker contains water and steam in equilibrium at a pressure greater than atmospheric pressure. How does this greater pressure increase cooking speed?
Explain why the formation of condensation on a glass filled with ice water is a warming process. What warms when condensation forms? Explain.
Perspiration is usually followed by evaporation which cools the body. Explain why evaporation is a cooling process. What cools when perspiration evaporates? Explain.
Why does steam cause a more severe burn than hot water?
Why does water boil when placed in a vacuum chamber and the air pressure is reduced? See the video.

problems

[openstax univ. phys. vol.2 – 1.89] The walls of a house are 13.0 cm thick and have an average thermal conductivity twice that of glass wool. Assume there are no windows or doors. The walls’ surface area is 120m² and their inside surface is at 18.0ºC, while their outside surface is at 5.00ºC.
1. Calculate the rate of heat conduction through the walls.
2. How many 1.00-kW room heaters would be needed to balance the heat transfer due to conduction?
[openstax univ. phys. vol. 2 – 1.91] Calculate the rate of heat conduction out of the human body, assuming that the core internal temperature is 37.0ºC, the skin temperature is 34.0ºC, the thickness of the fatty tissues between the core and the skin averages 1.00 cm, and the surface area is 1.40m².
[openstax univ. phys. vol. 2 – 1.92] Suppose you stand with one foot on ceramic flooring and one foot on a wool carpet, making contact over an area of 80.0 cm²with each foot. Both the ceramic and the carpet are 2.00 cm thick and are10.0ºC on their bottom sides. At what rate must heat transfer occur from each foot to keep the top of the ceramic and carpet at33.0ºC? Take the thermal conductivity of ceramic to be the same as glass.
[openstax univ. phys. vol. 2 – example 1.13] What is the rate of heat transfer by radiation of an unclothed person standing in a dark room whose ambient temperature is 22.0ºC? The person has a normal skin temperature of 33.0ºC and a surface area of 1.50m². The emissivity of skin is 0.97 in the infrared, the part of the spectrum where the radiation takes place.
[openstax univ. phys. vol. 2 – 1.67] The number of kilocalories in food is determined by calorimetry techniques in which the food is burned and the amount of heat transfer is measured.
1. How many kilocalories per gram are there in a 5.00-g peanut if the energy from burning it is transferred to 0.500 kg of water held in a 0.100-kg aluminum cup, causing a 54.9ºC temperature increase? Assume the process takes place in an ideal calorimeter, in other words, a perfectly insulated container.
2. Compare your answer to the following labeling information found on a package of dry roasted peanuts: a serving of 33 g contains 200 calories. Comment on whether the values are consistent.
[openstax univ. phys. vol.2 – 1.70] A 1.28-kg sample of water at 10.0ºC is in a calorimeter. You drop a piece of steel with a mass of 0.385 kg at 215°C into it. After the sizzling subsides, what is the final equilibrium temperature? (Make the reasonable assumption that any steam produced condenses into liquid water during the process of equilibration and that the evaporation and condensation don’t affect the outcome, as we’ll see in the next section.)
[openstax univ. phys. vol. 2 – 1.73] A bag containing 0ºC ice is much more effective in absorbing energy than one containing the same amount of 0ºC water.
1. How much heat transfer is necessary to raise the temperature of 0.800 kg of water from 0ºC to 30.0ºC?
2. How much heat transfer is required to first melt 0.800 kg of 0ºC ice and then raise its temperature to 30.0°C?
3. Explain how your answer supports the contention that the ice is more effective.
[openstax univ. phys. vol. 2 – 1.74]
1. How much heat transfer is required to raise the temperature of a 0.750-kg aluminum pot containing 2.50 kg of water from 30.0ºC to the boiling point and then boil away 0.750 kg of water?
2. How long does this take if the rate of heat transfer is 500 W?
[openstax univ. phys. vol. 2 – 1.83]To help prevent frost damage, 4.00 kg of water at 0°C is sprayed onto a fruit tree.
1. How much heat transfer occurs as the water freezes?
2. How much would the temperature of the 200-kg tree decrease if this amount of heat was transferred from the tree? Take the specific heat to be 3.35kJ/kgºC, and assume that no phase change occurs in the tree.
[openstax univ. phys. vol. 2 – 1.84] A 0.250-kg aluminum bowl holding0.800kg of soup at 25.0ºC is placed in a freezer. What is the final temperature if 388 kJ of energy is transferred from the bowl and soup, assuming the soup’s thermal properties are the same as that of water?
[openstax univ. phys. vol. 2 – 1.86] You pour 0.0100 kg of 20.0ºC water onto a 1.20-kg block of ice which is initially at-15.0ºC, what is the final temperature? You may assume that the water cools so rapidly that the effects of the surroundings are negligible.
[Jeffrey Schnick SAC136] – Approximately how much heat would it take to change 0.130 kg of ice (solid water) at -12.0 ºC to water vapor (water in gaseous form) at 112.0 ºC?
[Jeffrey Schnick SAC136] – A 467-gram chunk of solid water (ice) at -12.5 °C is put into a Styrofoam bucket which has some liquid water at 24.0 °C in it. A lid is put on the bucket. The heat capacity of the bucket is negligible. Heat flow into or out of the water from or to the surroundings is also negligible. When equilibrium is reached, the bucket is found to contain only liquid water at 1.2 °C. At that point, how much water, by mass, is in the bucket?
A block of ice with a temperature of 0 °C covers the upper surface of a 2400 cm² slab of stone with a thickness of 10.0cm. The slab is exposed to steam at 100 °C on the lower surface. Find the heat conductivity of stone if 5.00kg of ice is melted in one hour.
A cylindrical piece of steel is 10.0 cm thick, When the temperature difference between the two ends is 20.0ºF, heat is transferred from one end to the other end at a rate of 50.0W. Find the area of the circular surface of the cylinder.
The radiator of a car that is at 110°C transfers energy into the 30.0°C environment. Calculate the rate of heat transfer by radiation if the radiator has an emissivity of 0.750 and a surface area of 1.20m².

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

heat – flow of thermal energy

Conduction

Convection

Radiation

calorimetry- Temperature change and Phase change

Attribution

questions and problems

questions

problems

License

Share This Book