Unit 10 – Work and Kinetic Energy

Beta Keramati

Work and Energy

Last Update: 12/02/2022

work

Work is a process where a system’s energy changes.

The scientific definition of work differs in some ways from its everyday meaning. For work, in the scientific sense, to be done, a force must be exerted and there must be displacement in the direction of the force. When a force does work on a system, the energy of that system changes. We will examine the relationship between work and energy in the next section.

Formally, the work done on a system by a constant force is defined to be the product of the component of the force in the direction of motion times the distance through which the force acts. For one-way motion in one dimension, this is expressed in equation form as

$\boxed{W=FdCos\theta}$ Work done by a constant force

Where W is work, d is the magnitude of the displacement of the system, F is the magnitude of the force, and Θ is the angle between the force vector F and the displacement vector d. So FCosΘ is the component of the force parallel to displacement.

To find the work done on a system that undergoes motion that is not one-way or that is in two or three dimensions, we divide the motion into one-way one-dimensional segments and add up the work done over each segment.

Work is a scalar quantity, but it can be positive or negative depending on the angle between the force vector and the displacement vector. If work is positive, energy is added to the system; if negative, energy is taken away.

Let’s examine work done in various situations depicted in Figure 10.1.

In Figure 10.1(a), the work done by the force F on this lawnmower is Fd cosθ. Note that F cosθ is the component of the force in the direction of motion. $W=FdCos\theta$

In Figure 10.1(b) A person holding a briefcase applies force F on the briefcase. This force does no work on the briefcase because there is no displacement. No energy is transferred to or from the briefcase. $W=F(0)Cos\theta=0$

In Figure 10.1(c), the person moving the briefcase horizontally at a constant speed applies force F on the briefcase. This force does no work on the briefcase because F does not have a component in the direction of displacement, d. $W=FdCos90^{\circ}=Fd(0)=0$

In Figure 10.1(d), work is done on the briefcase by carrying it upstairs at a constant speed. The person applies force F on the briefcase, and this force has a component in the direction of displacement, d. In this process, energy is transferred to the briefcase. $W=FdCos\theta$

In Figure 10.1(e), when the briefcase is lowered, energy is transferred out of the briefcase and into an electric generator. Here the work done on the briefcase by force F is negative because F is in the opposite direction of displacement, d. Negative work means energy is removed from the briefcase. $W=FdCos180^{\circ} =-Fd$

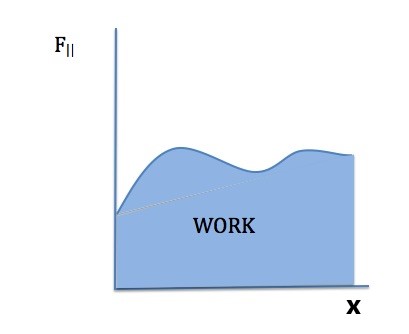
Now, let’s consider the graphical representation of work. When a constant force does work, work is calculated with W=FdCosΘ. As mentioned earlier, FCosΘ is the component of force along the direction of displacement. For a constant force, the graph of FCosΘ vs d is

The area under the line represents work. This idea can be extended to any force, whether constant or not.

The component of force along the direction of displacement, FCosΘ, can be also represented with the symbol F_||. The area under the plot of F_|| (the component of force parallel to displacement) vs x (position) is work.

Work and energy have the same units. From the definition of work, we see that those units are units of force times units of distance. Thus, in SI units, work and energy are measured in newton-meters. A newton-meter is given the special name joule(J), and

$1J=1Nm=1kgm^2/s^2$

One joule is not a large amount of energy; it would lift a small 100-gram apple a distance of about 1 meter.

Sometimes energy is measured in calories. One calorie (1 cal) is the energy required to warm 1 g of water by 1°C and is equivalent to 4.184J, while one food calorie (1 kcal) is equivalent to 4184J.

Example 10.1 – Calculating the Work You Do to Push a Lawn Mower Across a Large Lawn

How much work is done on the lawnmower by the person in Figure 10.1(a) if he exerts a constant force of 75.0N at an angle of 35.0° below the horizontal and pushes the mower 25.0m on level ground? Convert the amount of work from joules to kilocalories and compare it with this person’s average daily intake of 2400kcal of food energy.

Solution

The equation for the work is

$W=Fdcos\theta$

Substituting the known values gives

$W=(75.0N)(25.0m)cos35.0^\circ$

$W=1536J=1.54\times 10^3J$

Converting the work in joules to kilocalories yields

$W=1536J\times \frac{1kcal}{4184J}$

$W=0.367kcal$

The ratio of the work done to the daily consumption is

$\frac{0.367kcal}{2400kcal}=1.53\times 10^{-4}$

Discussion

This ratio is a tiny fraction of what the person consumes, but it is typical. Very little of the energy released in the consumption of food is used to do work. Even when we “work” all day long, less than 10% of our food energy intake is used to do work and more than 90% is converted to thermal energy or stored as chemical energy in fat.

Video Example – Pushing a box up an incline

Example 10.2

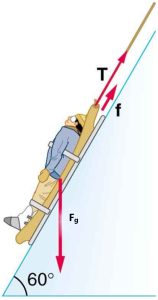
Suppose the ski patrol lowers a rescue sled and victim, having a total mass of 90.0 kg, down a 60° slope at a constant speed, as shown in Figure 10.4. The coefficient of friction between the sled and the snow is 0.100. (a) How much work is done by friction as the sled moves 30.0 m along the hill? (b) How much work is done by the rope on the sled in this distance? (c) What is the work done by the gravitational force on the sled? (d) What is the total work done?

Solution

In order to determine the work done by each force, we must first determine the magnitude of each force. To do this, we must apply Newton’s Second Law.

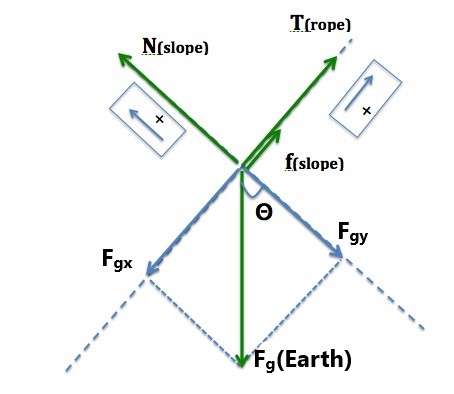
Step 1 – The free-body diagram for the person is shown in Figure 10.5

Step 2 – If the person were to accelerate, the acceleration would be parallel to the slope. So we take the x-axis to be parallel to the slope with the positive direction pointing up the slope, and the y-axis perpendicular to the slope with the positive direction in the direction of the normal force, N.

Step 3 – Let’s calculate the components of the gravitational force, W. Notice that Θ=60°.

$Sin 60^\circ =\frac{-F_{gx}}{F_g}$

$F_{gx}= -F_gSin 60^\circ$

$F_{gx} = -(90.0kg)(9.8m/s^2)Sin 60^\circ$

$F_{gx}=- 763.8 N$

$Cos 60^\circ =\frac{-F_{gy}}{F_g}$

$F_{gy}= -F_gCos60^\circ$

$F_{gy}= -(90.0kg)(9.8m/s^2)Cos 60^\circ$

$F_{gy} = -441.0 N$

Step 4 and Step 5 – Applying Newton’s Second Law in x and y directions yield

$x-direction$

$y-direction$

$a_x=\frac{\sum F_x}{m}$

$0=\frac{-763.8N + f+T}{90.0kg}$

$a_y=\frac{\sum F_y}{m}$

$0=\frac{N-441.0N}{90.0kg}$

$N=441.0N$

Since friction is kinetic friction, and μ_k=0.100

$f_k = \mu_k N$

$f = (0.100)(441.0N)$

$f = 44.1N$

Putting it all together we get

$0=\frac{-763.8N + f+T}{90.0kg}$

$0=\frac{-763.8N + 44.10N+T}{90.0kg}$

$T=719.7N$

Solution for (a)

Work done by friction force is

$W=FdCos\theta$

$W_f=(44.1N)(30.0m)Cos(180^\circ)$

$W_f=-1323J$

Solution for (b)

Work done by the tension force of the rope is

$W=FdCos\theta$

$W_T=(719.7N)(30.0m)Cos(180^\circ)$

$W_T=-21591J$

Solution for (c)

Work done by the gravitational force, F_g is

$W=FdCos\theta$

$W_{F_g}=(90.0kg)(9.8m/s^2)(30.0m)Cos(30^\circ)$

$W_{F_g}=22914J$

Solution for (d)

Total work is the algebraic sum of the work done by all the forces. Notice that since the normal force is perpendicular to the displacement, the work done by the normal force is zero.

$W_{total}=-1323J-21591J+22914J$

$W_{total}=0J$

Example 10.3

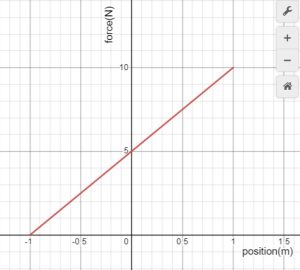
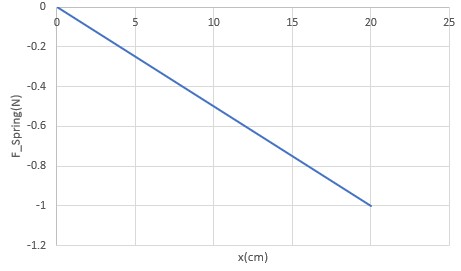
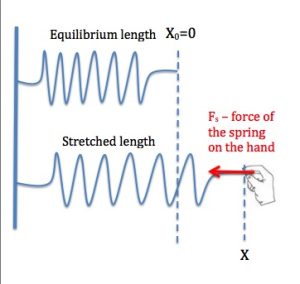
As we saw in Unit 8 the elastic force of a spring is a variable force. Since the magnitude of this force is directly proportional to the change in length of the spring and its direction is always opposite to the direction in which the spring has been stretched or compressed, this force can be expressed as F_spring=-Kx. For spring, the graph of F_spring vs change in length of the spring, x, is given below. How much work is done by the spring while a person stretches the spring from its equilibrium length (x=0) to 20cm?

Solution

Since this is not a constant force we can’t use the equation $W=FdCos\theta$ to calculate work. But since we have the graph of F vs x we can find work by calculating the area under the blue line.

The area is in the shape of a triangle.

$Work = Area = \frac{1}{2}(0.20m)(-1N)$

$Work = -0.1J$

Notice that while the spring is being stretched the force of the spring does negative work, while the force applied by the hand is doing positive work.

work-energy theorem

As mentioned earlier, work is a process through which energy is transferred into or out of a system. There is a very close relationship between work and energy. In this unit, we will examine this relationship.

One type of energy is kinetic energy. Kinetic energy is energy due to motion, and as long as the speed is significantly less than the speed of light, kinetic energy is given by

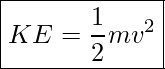$\boxed{KE=\frac{1}{2}mv^2}$ Kinetic Energy

Where m is the mass of the object and v is its speed.

To derive the relationship between work and energy we need to combine Newton’s Second Law with the kinematic relationships we found for motion with constant acceleration. To simplify, we will do this for one-dimensional motion and then generalize the result:

$a = \frac{\sum F}{m}$

$v^2 - v_0^2 = 2a \Delta x$ ⇒ $a= \frac{v^2 - v_0^2}{2 \Delta x}$

$\frac{v^2 - v_0^2}{2 \Delta x}=\frac{\sum F}{m}$

$(\sum F)(\Delta x)=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2$

Since in one dimension ΣF and Δx are parallel, we can replace the left hand side of the equation with net work, W_net.

$W_{net}=\frac{1}{2}mv^2 - \frac{1}{2}mv_0^2$

The left-hand side is the algebraic sum of work done by all the forces acting on a system, and the right-hand side is the change in the kinetic energy of that system.

$\boxed{ W_{net}=\Delta KE}$ Work-Energy Theorem

This is the most fundamental relationship between work and energy and is valid in all situations. Notice that when the net work on a system is positive, kinetic energy is added to, and when the net work is negative, kinetic energy is removed from the system.

Example 10.4

Let’s revisit Example 10.2 where the ski patrol lowers a rescue sled and victim down a slope with constant speed. In that example, we calculated the work done by each force and then added them all up to determine the total work and we found the total work to be zero. Notice that this result is consistent with the work-energy theorem. Since the speed is constant, there is no change in the kinetic energy, and therefore the net work must equal to zero.

Example 10.5 – Determining the work to accelerate a pacakage

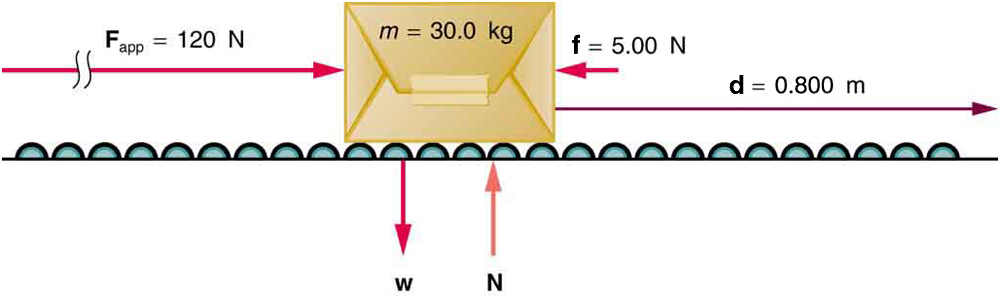
Suppose a 30.0-kg package on a roller belt conveyor system in Figure 10.7 is moving at 0.500 m/s. You push on it with a constant horizontal force of 120 N through a distance of 0.800 m and then you let it go. The opposing friction force averages 5.00 N.

a) Determine the net work done on this package while it is pushed through a distance of 0.800m.

b) When you stop pushing, the friction force causes the package to slow down. How far does the package move before it stops?

Solution for (a)

There are two ways to approach this problem.

Determine the work done by individual forces and add them up.
Determine the change in the kinetic energy and then use the work-energy theorem to find the net work.

Solution using method 1

For each force, we calculate work using

$W=FdCos\theta$

Work done by the gravitational force (W) and the work done by the normal force (F) are zero because both of these forces are perpendicular to the displacement.

Work done by the force applied by the person (F) is

$W_F=(120N)(0.800m)Cos(0)$

$W_F=96.0J$

Work done by the friction force (f) is

$W_f=(5.00N)(0.800m)Cos(180)$

$W_f=-4.00J$

The net work is the sum of these two works

$W_{net}=96.0J-4.00J$

$W_{net}=92.0J$

Alternatively, we could have found the net force first, and then calculated the work done by the net force

$W_{net}=F_{net}dCos\theta$

$W_{net}=(120N-5.00N)(0.800m)Cos(0)$

$W_{net}=92.0J$

Solution using method 2

To find the change in kinetic energy we need to find the speed of the package after it’s been pushed over a distance of 0.800m. To calculate this final speed, we need to find the acceleration, and this requires the application of Newton’s Second Law.

Step1- The free body diagram is given in Figure 10.8

Step 2 – The acceleration is horizontal. We pick the x and y axes horizontal and vertical with the positive directions as shown on the free body diagram.

Step 3 – All the forces are along the x and y axes. There is no component to draw or to calculate.

Step 4 and Step 5– Apply Newton’s Second Law in component form.

$x-direction$

$y-direction$

$a_x=\frac{\sum F_x}{m}$

$a_x=\frac{120N-5.00N}{30.0kg}$

$a_x=3.83m/s^2$

$a_y=\frac{\sum F_y}{m}$

$0=\frac{N-(30kg)(9.8m/s^2)}{30.0kg}$

$N=294N$

Now we can use the kinematics equation to find the final velocity.

$v^2 - v_0^2 = 2a \Delta x$

$v^2 - (0.500m/s)^2 = 2(3.83m/s^2)(0.800m)$

$v=2.53m/s$

We are now ready to use the work-energy theorem.

$W_{net}=\Delta KE$

$W_{net}=\frac{1}{2}mv^2 - \frac{1}{2}mv_0^2$

$W_{net}=\frac{1}{2}(30.0kg)(2.53m/s)^2 - \frac{1}{2}(30.0kg)(0.500m/s)^2$

$W_{net}=92.0J$

Solution for (b)

Once again, there are two ways to approach this problem.

We can use the work-energy theorem
We can use Newton’s Second Law, along with kinematics equations

Solution using method 1

Once the pushing force, F, stops, the only force doing work is the friction force, f.

$W_{net}=\Delta KE$

$W_f=\frac{1}{2}mv^2 - \frac{1}{2}mv_0^2$

$(5.00N)dCos(180^\circ)=\frac{1}{2}(30.0kg)(0m/s)^2 - \frac{1}{2}(30.0kg)(2.53m/s)^2$

$d=19.2m$

Solution using method 2

With only the friction force in the horizontal direction, applying Newton’s Second Law along the x-axis yields

$x-direction$

$a_x=\frac{\sum F_x}{m}$

$a_x=\frac{-5.00N}{30.0kg}$

$a_x=-0.167m/s^2$

We use kinematics equations to solve for the displacement

$(0m/s)^2 - (2.53m/s)^2 = 2(-0.167m/s^2)\Delta x$

$\Delta x=19.2m$

Discussion

Just like part (b) of this example, many mechanics problems can be solved by either applying the work-energy theorem or by using Newton’s Second Law and kinematics equations. Usually, when there is an option, the work-energy approach is the easiest way.

Video Example – Block Sliding up an incline

Attributions

This chapter contains material taken from Openstax College Physics-Work, Energy, and Energy Resources, by Openstax, and is used under a CC BY 4.0 license. Download this book for free at Openstax-College Physics.

To see what was changed, refer to the List of Changes.

problems

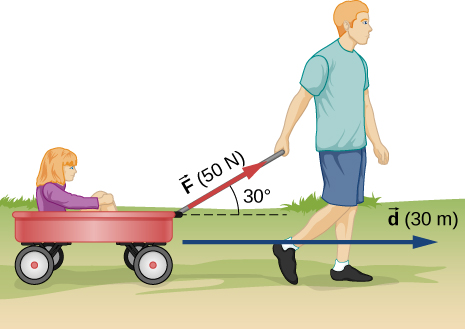
[openstax univ. phys. vol. 1 – 7.28] How much work is done by the boy pulling his sister 30.0 m in a wagon while applying a 50.0N force at a 30.0° angle as shown below?
[openstax univ. phys. vol. 1 – 7.29(edited)] A shopper pushes a grocery cart 20.0 m at constant speed on level ground with a force that makes a 25.0° angle below horizontal. The friction force between the cart and the ground is 35.0 N.
1. What is the work done on the cart by the friction force?
2. What is the work done on the cart by the gravitational force?
3. Find the force the shopper exerts, using the work-energy principle.
[openstax univ. phys. vol. 1 – 7.34] A boy pulls a sled with a total mass of 50.0 kg, 20.0 m across the snow at a constant velocity by applying a force that makes a 25.0º angle above the horizontal. The coefficient of kinetic friction between the sled and the snow is 0.200.
1. Calculate the work done by the applied force.
2. Calculate the work of friction.
3. Calculate the total work.
A box of mass 8.00kg, starting from rest, is being pushed up a 30.0° incline with a horizontal force that has a magnitude of 70.0N. The coefficient of kinetic friction between the box and the incline is 0.170.
1. Find the work done by each force acting on the box while the box slides up a distance of 1.50m along the incline.
2. Use the work-energy principle to find the final speed of the box.
  
  Problems 5 through 8 can be solved in two different ways. You can either use the work-energy relationship, or you could use Newton’s Second Law to find the acceleration, and then use the kinematics equations. You are expected to know both methods.
[openstax univ. phys. vol. 1 – 7.50]
1. Calculate the force needed to bring a 950-kg car to rest from a speed of 90.0 km/h in a distance of 120 m (a fairly typical distance for a non-panic stop).
2. Suppose instead the car hits a concrete abutment at full speed and is brought to a stop in 2.00 m. Calculate the force exerted on the car and compare it with the force found in part (a).
[openstax univ. phys. vol. 1 – 7.55]A constant 10.0 N horizontal force is applied to a 20.0 kg cart at rest on a level floor. If friction is negligible, what is the speed of the cart when it has been pushed 8.00 m?
[openstax univ. phys. vol. 1 – 7.56] A constant force of 10.0 N force is applied at an angle of 45.0º below the horizontal to a 20.0kg cart at rest on a level floor. What is the speed of the cart when it has been pushed 8.00 m?
[openstax univ. phys. vol. 1 – 7.58]A wagon with its passenger sits at the top of a hill. The wagon starts from rest and rolls 100 m down a 10.0º incline to the bottom of the hill. What is the wagon’s speed when it reaches the end of the incline? Assume that the retarding force of friction is negligible.
A variable force acts on a 5.00kg object that is initially moving with a speed of 8.00m/s. Assuming this is the only force doing work, first use the graph of force vs position to determine the work done by this force, then use the work-energy principle to determine the final speed of the object.
1. 1. graph of force vs position
  2. graph of force vs position
  3. graph of force vs position

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

work

work-energy theorem

Attributions

problems

License

Share This Book