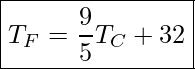UNIT 16 – Temperature, Thermal Expansion, Ideal Gas Law, and Kinetic Theory

Beta Keramati

Temperature and Heat Transfer

Last Update: 08/29/2023

temperature and the zeroth law of thermodynamics

Temperature is operationally defined to be what we measure with a thermometer. In this section, we discuss temperature, its measurement by thermometers, and its relationship to thermal equilibrium.

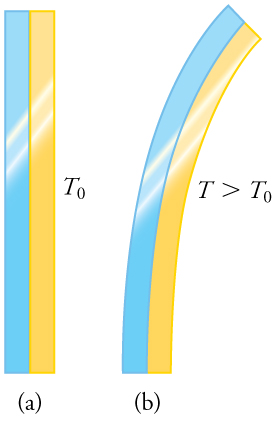
Any physical property that depends on temperature, and whose response to temperature is reproducible, can be used as the basis of a thermometer. Because many physical properties depend on temperature, the variety of thermometers is remarkable. For example, volume increases with temperature for most substances. This property is the basis for the common alcohol thermometer, the old mercury thermometer, and the bimetallic strip (Figure 16.1). Other properties used to measure temperature include electrical resistance and color, as shown in Figure 16.2, and the emission of infrared radiation, as shown in Figure 16.3.

Figure 16.1 -The curvature of a bimetallic strip depends on temperature. (a) The strip is straight at the starting temperature, where its two components have the same length. (b) At a higher temperature, this strip bends to the right, because the metal on the left has expanded more than the metal on the right.

Figure 16.2 -Each of the six squares on this plastic (liquid crystal) thermometer contains a film of a different heat-sensitive liquid crystal material. Below 95ºF, all six squares are black. When the plastic thermometer is exposed to a temperature that increases to 95ºF, the first liquid crystal square changes color. When the temperature increases above 96.8ºF the second liquid crystal square also changes color, and so forth. (credit: Arkrishna, Wikimedia Commons)

Figure 16.3 – USS KITTY HAWK (CV 63), At Sea (Aug. 24, 2004) – Fireman Jason Ormand of Yukon, Okla., checks the temperature of a ventilation system while conducting a routine trouble call aboard USS Kitty Hawk (CV 63). Assigned to the air conditioning and repair shop, Ormand helps maintain eight air conditioning machinery spaces aboard Kitty Hawk. Currently, underway in the 7th Fleet area of responsibility (AOR), Kitty Hawk demonstrates power projection and sea control as the world’s only permanently forward-deployed aircraft carrier, operating from Yokosuka, Japan.
U.S. Navy photo by Photographer’s Mate 3rd Class Lamel J. Hinton

THE ZEROTH LAW OF THERMODYNAMICS

An important concept related to temperature is thermal equilibrium. Two objects are in thermal equilibrium if they are in close contact that allows either to gain thermal energy from the other, but nevertheless, no net thermal energy is transferred between them. Even when not in contact, they are in thermal equilibrium if, when they are placed in contact, no net thermal energy is transferred between them. If two objects remain in contact for a long time, they typically come to equilibrium. In other words, two objects in thermal equilibrium do not exchange thermal energy. You can think of “thermal energy” as being energy related to the random motion of molecules and transferred between substances at a molecular level.

Experimentally, if object A is in equilibrium with object B, and object B is in equilibrium with object C, then (as you may have already guessed) object A is in equilibrium with object C. That statement of transitivity is called the zeroth law of thermodynamics. (The number “zeroth” was suggested by British physicist Ralph Fowler in the 1930s. The first, second, and third laws of thermodynamics were already named and numbered then. The zeroth law had seldom been stated, but it needs to be discussed before the others, so Fowler gave it a smaller number.) Consider the case where A is a thermometer. The zeroth law tells us that if A reads a certain temperature when in equilibrium with B, and it is then placed in contact with C, it will not exchange energy with C; therefore, its temperature reading will remain the same. In other words, if two objects are in thermal equilibrium, they have the same temperature.

temperature scales

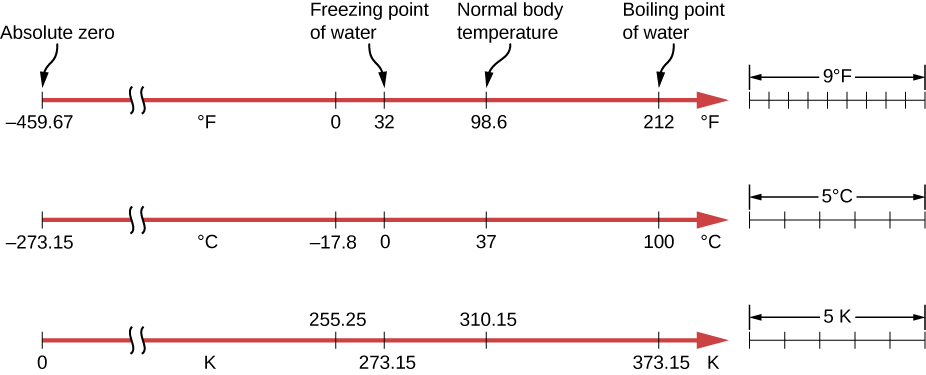
The three most common temperature scales are the Fahrenheit, Celsius, and Kelvin scales. A temperature scale can be created by identifying two easily reproducible temperatures. The freezing and boiling temperatures of water at standard atmospheric pressure are commonly used.

The Celsius scale has the freezing point of water at 0°C and the boiling point at 100°C. Its unit is the degree Celsius °C. On the Fahrenheit scale, the freezing point of water is at 32°F and the boiling point is at 212°F. The unit of temperature on this scale is the degree Fahrenheit °F. Note that a temperature difference of one degree Celsius is greater than a temperature difference of one degree Fahrenheit. Only 100 Celsius degrees span the same range as 180 Fahrenheit degrees, thus one degree on the Celsius scale is 1.8 times larger than one degree on the Fahrenheit scale.

The Kelvin scale is the temperature scale that is commonly used in science. It is an absolute temperature scale defined to have 0 K at the lowest possible temperature, called absolute zero. The official temperature unit on this scale is the kelvin, which is abbreviated K and is not accompanied by a degree sign. The freezing and boiling points of water are 273.15 K and 373.15 K, respectively. Thus, the magnitude of temperature differences is the same in units of kelvins and degrees Celsius. Unlike other temperature scales, the Kelvin scale is an absolute scale. It is used extensively in scientific work because a number of physical quantities, such as the volume of an ideal gas, are directly related to absolute temperature. The kelvin is the SI unit used in scientific work.

Absolute zero is the temperature at which all molecular motion has ceased. The concept of absolute zero arises from the behavior of gases. Figure 16.4 shows how the pressure of gases at a constant volume decreases as temperature decreases. Various scientists have noted that the pressures of gases extrapolate to zero at the same temperature, -273.15°C. This extrapolation implies that there is a minimum temperature. This temperature is called absolute zero. Today we know that most gases first liquefy and then freeze, and it is not actually possible to reach absolute zero. The numerical value of absolute zero temperature is -273.15°C or 0 K.

The relationships between the three common temperature scales are shown in Figure 16.5.

$\boxed{T_F=\frac{9}{5}T_C+32}$

$\boxed{T_K=T_C+273.15}$

Example 16.1 – Converting Between Temperature Scales: Room Temperature

A comfortable room temperature is 70°F. Express this temperature in Kelvin.

Solution

We first need to convert this temperature to °C.

$T_F=\frac{9}{5}T_C+32$

$70=\frac{9}{5}T_C+32$

$\frac{5}{9}(70-32)=T_C$

$T_C=21^\circ C$

Now, we can use the relationship between °C and K.

$T_K=T_C+273.15$

$T_K=21+273.15$

$T_K=294 K$

Human Body Temperature

Thermoregulation is the ability of an organism to keep its body temperature within certain boundaries, even when the surrounding temperature is very different. A thermoconforming organism, by contrast, simply adopts the surrounding temperature as its own body temperature, thus avoiding the need for internal thermoregulation. The internal thermoregulation process is one aspect of homeostasis: a state of dynamic stability in an organism’s internal conditions maintained far from thermal equilibrium with its environment. If the body is unable to maintain a normal temperature and it increases significantly above normal, a condition known as hyperthermia occurs. For humans, this occurs when the body is exposed to constant temperatures of approximately 55 °C (131 °F), and with prolonged exposure (longer than a few hours) at this temperature and up to around 75 °C (167 °F) death is almost inevitable. The opposite condition, when body temperature decreases below normal levels, is known as hypothermia. It results when the homeostatic control mechanisms of heat within the body malfunction, causing the body to lose heat faster than producing it. Normal body temperature is around 37 °C (99 °F), and hypothermia sets in when the core body temperature gets lower than 35 °C (95 °F). Usually caused by prolonged exposure to cold temperatures, hypothermia is usually treated by methods that attempt to raise the body temperature back to a normal range.

thermal expansion of solids and liquids

As we will see in the next section, an increase in temperature implies an increase in the kinetic energy of the individual atoms. In a solid, unlike in a gas, the atoms or molecules are closely packed together, and their kinetic energy in the form of small, rapid vibrations, pushes neighboring atoms or molecules apart from each other. This neighbor-to-neighbor pushing results in a slightly greater distance, on average, between neighbors, and adds up to a larger size for the whole body. For most substances under ordinary conditions, there is no preferred direction, and an increase in temperature will increase the solid’s size by a certain fraction in each dimension.

In one dimension, the change in length ΔL due to thermal expansion is proportional to the initial length, L₀, and the change in temperature, ΔT. The change in length is also dependent on the type of material. The equation reflecting these relationships is

$\boxed{\Delta L=\alpha L_0 \Delta T}$ Linear Thermal Expansion

In this equation, $\alpha$ is the coefficient of linear expansion, and its numerical value for various substances is given in Table 16.1.

Table 16.1

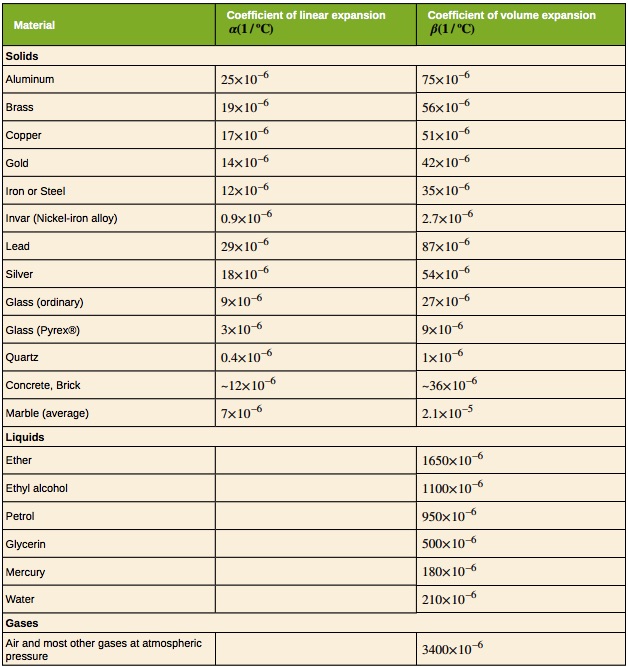
Objects expand in all dimensions, as illustrated in Figure 16.6. That is, their areas and volumes, as well as their lengths, increase with temperature. Holes also get larger with temperature. If you cut a hole in a metal plate, the remaining material will expand exactly as it would if the plug was still in place. The plug would get bigger, and so the hole must get bigger too. Think of the ring of neighboring atoms or molecules on the wall of the hole as pushing each other farther apart as temperature increases. Obviously, the ring of neighbors must get slightly larger, so the hole gets slightly larger.

For small temperature changes, the change in the area, ΔA, is given by

$\boxed{\Delta A=2 \alpha A_0 \Delta T}$ Thermal Expansion of Area

where A₀ is the initial area.

The change in volume, ΔV, is given by

$\boxed{\Delta V= \beta V_0 \Delta T}$ Thermal Expansion of Volume

For solids, the coefficient of volume expansion, $\beta$ is very nearly three times the coefficient of linear expansion. $\beta=3\alpha$

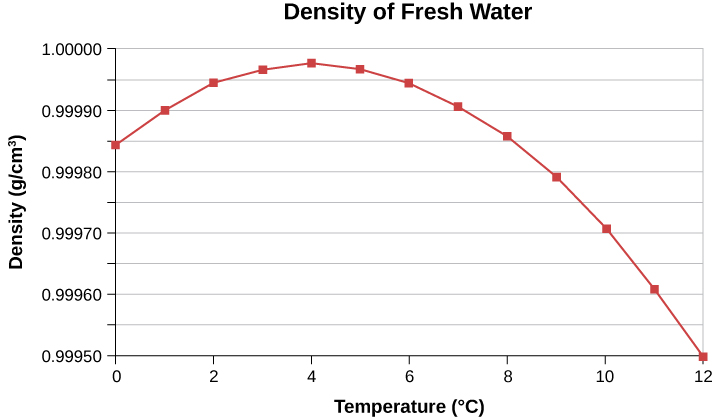
In general, objects will expand with increasing temperature. Water is the most important exception to this rule. Water expands with increasing temperature (its density decreases) when it is at temperatures greater than 4°C. However, it expands with decreasing temperature when it is between +4°C and 0°C. Water is densest at +4°C. This is shown in Figure 16.7. Perhaps the most striking effect of this phenomenon is the freezing of water in a pond. When water near the surface cools down to 4°C, it is denser than the remaining water and thus will sink to the bottom. This “turnover” results in a layer of warmer water near the surface, which is then cooled. Eventually, the pond has a uniform temperature of 4ºC. If the temperature in the surface layer drops below 4ºC, the water is less dense than the water below, and thus stays near the top. As a result, the pond surface can completely freeze over. The ice on top of liquid water provides an insulating layer from winter’s harsh exterior air temperatures. Fish and other aquatic life can survive in 4°C water beneath the ice, due to this unusual characteristic of water. It also produces circulation of water in the pond which is necessary for a healthy ecosystem of the body of water.

Example 16.2

The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from -15ºC and 40ºC. What is the change in length between these temperatures? Assume that the bridge is made entirely of steel.

Solution

Use the equation for linear thermal expansion Δ𝐿=𝛼𝐿Δ𝑇 to calculate the change in length, Δ𝐿. Use the coefficient of linear expansion 𝛼 for steel from Table 16.1, and note that the change in temperature Δ𝑇 is 55°C.

$\Delta L=\alpha L \Delta T$

$\Delta L=12\times 10^{-6}(\frac{1}{^\circ C})(1275m)(55^\circ C)$

$\Delta L=0.84m$

Discussion
Although not large compared with the length of the bridge, this change in length is observable. It is generally spread over many expansion joints so that the expansion at each joint is small.

Example 16.3

Suppose a 60.0-L steel gasoline tank is full of gas that is cool because it has just been pumped from an underground reservoir. Now, both the tank and the gasoline have a temperature of 15ºC. How much gasoline has spilled by the time they warm to 35ºC?

Solution

The tank and gasoline increase in volume, but the gasoline increases more, so the amount spilled is the difference in their volume changes. We can use the equation for volume expansion to calculate the change in volume of the gasoline and of the tank. (The gasoline tank can be treated as solid steel.)

Use the equation for volume expansion to calculate the increase in the volume of the steel tank:

$\Delta V_s= \beta_s V_{0s} \Delta T$

The increase in volume of the gasoline is given by this equation:

$\Delta V_{gas}= \beta V_{0gas} \Delta T$

Find the difference in volume to determine the amount spilled as:

$V_{spill}= \Delta V_{gas}- \Delta V_s$

$V_{spill}= \beta V_{0gas} \Delta T- \beta_s V_{0s} \Delta T$

$V_{spill}= 950 \times 10^{-6} (\frac{1}{^\circ C})(60.0L)(20^\circ C)- 35 \times 10^{-6} (\frac{1}{^\circ C})(60.0L)(20^\circ C)$

$V_{spill}= 1.10L$

Discussion

This amount is significant, particularly for a 60.0-L tank. The effect is so striking because gasoline and steel expand quickly. If you try to cap the tank tightly to prevent overflow, you will find that it leaks anyway, either around the cap or by bursting the tank. Tightly constricting the expanding gas is equivalent to compressing it, and both liquids and solids resist compression with extremely large forces. To avoid rupturing rigid containers, these containers have air gaps, which allow them to expand and contract without stressing them.

ideal gas law

In this section, we explore the thermal behavior of gases. Gases are easily compressed. We can see evidence of this in Table 16.1, where you will note that gases have the largest coefficient of volume expansion. The large coefficient means that gases expand and contract very rapidly with temperature changes. In addition, you will note that most gases expand at the same rate, or have the same coefficient of volume expansion, $\beta$ . This raises the question as to why gases should all act in nearly the same way when liquids and solids have widely varying expansion rates. The answer lies in the large separation of atoms and molecules in gases, compared to their size. If the temperature of a gas is not too high and/or its pressure too low, it is safe to assume the separation between molecules is so large that all forces between them except for collision forces can be ignored. In contrast, in liquids and solids, atoms and molecules are closer together and the forces between them are stronger.

An ideal gas is an idealized model of how a gas behaves. In this model, an ideal gas is a gas that consists of molecules with separation distances much larger than their size. Furthermore, according to this model, these molecules interact only when they collide, and the collisions between the molecules and the molecules and the walls of the container are all elastic. The ideal gas model is a very useful model because it correctly predicts the behavior of all gases in most situations. In this book, we will only discuss the behavior of gases as described by the ideal gas model.

The relationship between pressure, volume, temperature, and the number of molecules of an ideal gas was first found experimentally and is known as the Ideal Gas Law.

$\boxed{PV=Nk_BT}$ Ideal Gas Law

In this equation,

$P$ is the absolute pressure ( $Pressure=\frac{force}{volume}$ ), and is measured in units of Pascal (Pa). Pa=N/m³

$V$ is the volume which is the amount of space the gas occupies and is measured in units of m³

$N$ is the number of molecules of gas

$k_B$ is the Boltzmann Constant. $k_B= 1.38\times 10^{-23}J/K$

$T$ is the absolute temperature of the gas in Kelvin

Example 16.2 – Tire Pressure

Suppose your bicycle tire is fully inflated, with an absolute pressure of 7.00×10⁵Pa, at a temperature of 18.0°C. What is the pressure after its temperature has risen to 35.0°C? Assume that there are no appreciable leaks or changes in volume.

Solution

We know that P₁=7.00×10⁵Pa at a temperature of T₁=18.0°C. We are trying to find P₂ at a temperature of T₂=35.0°C. As the gas transitions from state (1) to state (2) its number of molecules and volume stay constant.

For each state, we can relate P, T, V, and N using the ideal gas law.

$P_1V_1=N_1k_BT_1$

$P_2V_2=N_2k_BT_2$

Since volume and number of molecules don’t change, we don’t need to use a subscript to distinguish their initial and final values. This means

$V_1=V_2=V$ and $N_1=N_2=N$

Making these substitutions in the ideal gas law equation for each state, and putting all the constants on one side we get

$P_1V=Nk_BT_1\ \Rightarrow\ \ \frac{P_1}{T_1}=\frac{Nk_b}{V}$

$P_2V=Nk_BT_2\ \Rightarrow\ \ \frac{P_2}{T_2}=\frac{Nk_b}{V}$

Since the right-hand sides of the two equations are equal, the left-hand sides must also be equal

$\frac{P_1}{T_1}=\frac{P_2}{T_2}$

Before we put numbers in, we must make convert all units to standard units for the ideal gas law.

$T_1=18.0 + 273.15 \ \Rightarrow\ \ T_1=291K$

$T_2=35.0 + 273.15 \ \Rightarrow\ \ T_2=308K$

Therefore

$\frac{7.00 \times 10^5 Pa}{291K}=\frac{P_2}{308K}$

$P_2=7.41 \times 10^5 Pa$

In the Ideal Gas Law, $PV=Nk_BT$ , P is the absolute pressure of the gas. But when we use a tool to measure, let’s say, tire pressure, we are measuring the pressure of the air inside the tire relative to the atmospheric pressure, and not its absolute pressure. We call this the gauge pressure. Pressure can be measured in various units. Some common units are pascal (Pa), atmosphere (atm), pound per square inch (psi), and millimeter of mercury (mmHg). The pressure applied by the column of air above us at sea level is 1atm=1.013×10⁵ Pa. The relationship between the absolute pressure, P, and the gauge pressure, P_gauge is:

$\boxed{P=P_{gauge} + 1 atm}$

Example 16.3 – Number Of Air Molecules In a Bicycle Tire

A bicycle tire has a volume of 1.35L and a gauge pressure of 60.0psi at 72.0°F. Find the number of air molecules in this tire.

Solution

We can use the Ideal Gas Law to solve for N, the number of molecules. But first, we have to put all the given parameters in the appropriate units.

Volume must be in m³.

$V=1.35L \times \frac{1 m^3}{1000L}$

$V=1.35\times 10^{-3} m^3$

Pressure has to be absolute pressure in Pascal.

$P_{gauge}=60.0 psi \times \frac{6894.76 Pa}{1psi}$

$P_{gauge}=4.14\times 10^{5} Pa$

$P=P_{gauge} + 1.013 \times 10^5 Pa$

$P=4.14\times 10^{5} Pa + 1.013 \times 10^5 Pa$

$P=5.15 \times 10^5 Pa$

Temperature has to be in Kelvin.

$T_F=\frac{9}{5}T_C+32$

$72.0=\frac{9}{5}T_C+32$

$T_C =\frac{5}{9}(72.0 - 32)$

$T_C =22.2^\circ C$

$T_K=T_C+273.15$

$T_K=22.2+273.15$

$T_K=295K$

Now we are ready to use the Ideal Gas Law

$PV=Nk_BT$

$(5.15 \times 10^5 Pa)(1.35\times 10^{-3} m^3)=N(1.38 \times 10^{-23}J/K)(295K)$

$N=1.71 \times 10^{23 }\ molecules$

Discussion

That is a HUGE number of molecules. It is 171,000,000,000,000,000,000,000 molecules!!! That’s roughly 20,000,000,000,000 times the population of Earth.

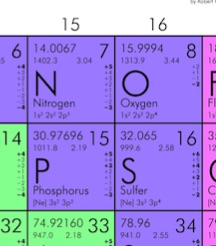
In the Ideal Gas Law equation, $PV=Nk_BT$ , N is the number of molecules in the gas. For any macroscopic sample of gas, the number of molecules is extremely large. Since doing calculations with very large numbers can be cumbersome, it is more convenient to group molecules into standard bundles, and keep track of the number of bundles instead of the number of molecules. The standard “bundle” to use in this context is called “mole”. One mole contains 6.02×10²³ molecules. The number of molecules in one mole is known as Avogadro’s number, N_A. In Example 16.3, the number of moles of air in the tire is $\frac{1.71 \times 10^{23 }}{6.02 \times 10^{23}}=0.284 mol$ . Furthermore, the mass of one mole of an element can be determined using the periodic table. Consider the following elements in the periodic table:

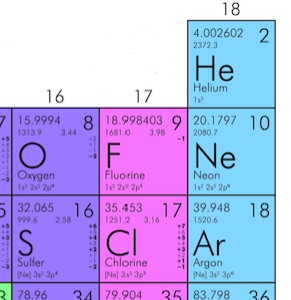
The number 4.002602 for Helium means that 1mol of He has a mass of 4.002602g. In other words, 6.02×10²³ atoms of He have a combined mass of 4.002602g. Since He is a monatomic gas, 1 mol of He gas has a mass of 4.002602g.

The number 15.9994 for Oxygen means that 1mol of O has a mass of 15.9994g. In other words, 6.02×10²³ atoms of O have a combined mass of 15.9994g. But since O is a diatomic gas, 1 mol of Oxygen gas is really 1 mol of O₂. Therefore, 1 mol of Oxygen gas has a mass of 2X(15.9994g)=31.9999g. In summary:

$N_A=6.02\times 10^{23}$ Avogadro’s Number

1 mol contains $6.02\times 10^{23}$ molecules.

The atomic mass of an element in “gram” Is the mass of 1 mol of the atoms of that element.

In order to express the Ideal Gas Law in terms of the number of moles instead of the number of molecules, we can divide and multiply the right-hand side by the Avogadro’s Number.

$PV=Nk_BT$

$PV=\frac{N}{N_A} N_A k_B T$

Notice that $\frac{N}{N_A}$ is the number of moles. We represent the number of moles with n. Therefore $\frac{N}{N_A}=n$ . Also $N_A k_B$ is a constant. We call this constant the Universal Gas Constant, and we represent it with R.

$R=N_A k_B$

$R=(6.02 \times 10^{23} molecules/mol)(1.38 \times10^{-23}J/K)$

$R=8.31J/mol.K$

Putting it all together, we get this alternative equation for the Ideal Gas Law.

$\boxed{PV=nRT}$ Ideal Gas Law

In this equation,

$P$ is the absolute pressure ( $Pressure=\frac{force}{volume}$ ), and is measured in units of Pascal (Pa). Pa=N/m³

$V$ is the volume which is the amount of space the gas occupies and is measured in units of m³

$n$ is the number of moles of gas

$R$ is the Universal Gas Constant. $R= 8.31J/mol.K$

$T$ is the absolute temperature of the gas in Kelvin

kinetic theory – relating pressure and temperature to molecular motion

In this section, we relate the macroscopic quantities of pressure and temperature to the motion of molecules in a sample of gas.

Figure 16.9 shows a box filled with gas.

The figure shows an expanded view of an elastic collision of a gas molecule with the wall of a container. Calculating the average force exerted by such molecules will lead us to the ideal gas law, and to the connection between temperature and molecular kinetic energy. We assume that a molecule is small compared with the separation of molecules in the gas, and that its interaction with other molecules can be ignored. We also assume the wall is rigid and that the molecule’s direction changes, but that its speed remains constant (elastic collision).

If the molecule’s velocity changes in the x-direction, its momentum changes from -mv_xto +mv_x. Thus, its change in momentum is $\Delta P=+mv_x -(-mv_x)=2mv_x$ . Using Newton’s Second Law, The force exerted on the molecule is given by

$F=\frac{\Delta P}{\Delta t}=\frac{2mv_x}{\Delta t}$

There is no force between the wall and the molecule until the molecule hits the wall. During the short time of the collision, the force between the molecule and the wall is relatively large. We are looking for an average force; we take $\Delta t$ to be the average time between collisions of the molecule with this wall. It is the time it would take the molecule to go across the box and back, a distance $2l$ at a speed of $v_x$ Thus $\Delta t=\frac{2l}{v_x}$ and the expression for the force becomes

$F=\frac{2mv_x}{\frac{2l}{V_x}}=\frac{mv_x^2}{l}$

This force is due to one molecule. We multiply by the number of molecules, N, and use their average squared velocity to find the force

$F=N\frac{m\overline{v_x^2}}{l}$

where the bar over a quantity means its average value. We would like to have the force in terms of the speed, v, rather than the x-component of the velocity. We note that the total velocity squared is the sum of the squares of its components, so that

$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}$

Because the velocities are random, their average components in all directions are the same:

$\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}$

Thus,

$\overline{v^2}=3\overline{v_x^2}$

or

\overline{v_x^2}= \frac{1}{3}\overline{v^2}

Substituting $\frac{1}{3}\overline{v^2}$ into the expression for F gives

$F=N\frac{m\overline{v^2}}{3l}$

The pressure is force per area, $P=\frac{F}{A}$ , so that we obtain

$P=\frac{F}{A}=N\frac{m\overline{v^2}}{3Al}=\frac{1}{3} \frac{Nm\overline{v^2}}{V}$

where we used V=Al for the volume. This gives the important result.

$PV=\frac{1}{3}Nm\overline{v^2}$

This equation is another expression of the Ideal Gas Law. It also relates the macroscopic quantity of pressure to the motion of molecules.

Since the other form of the Ideal Gas Law is $PV=Nk_BT$ , we can set the right-hand sides equal to one another to get

$\frac{1}{3}Nm\overline{v^2}=Nk_BT$

We can get the average kinetic energy of a molecule, $\frac{1}{2}mv^2$ , from the right-hand side of the equation by canceling N and multiplying by 3/2. This calculation produces the result that the average kinetic energy of a molecule is directly related to absolute temperature.

$\overline{KE}=\frac{1}{2}m\overline{v^2} = \frac{3}{2}k_B T$ Average Kinetic Energy Per Molecule

The equation above relates the macroscopic quantity of temperature to molecular motion. More specifically it shows that temperature is directly proportional to the average translational kinetic energy per molecule.

We can also rearrange the equation above to solve for, $\sqrt{\overline{v^2}}$ , root-mean-square (rms) speed, v_rms.

$\sqrt{\overline{v^2}}=v_{rms}=\sqrt{\frac{3k_B T}{m}}$

v_rms represents the average speed of molecules.

Section summary

What you need to take away from all these derivations in this section is that temperature is directly proportional to the average translational kinetic energy per molecule.

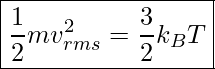$\boxed{\frac{1}{2}mv_{rms}^2 = \frac{3}{2}k_B T}$ Average Kinetic Energy Per Molecule & Absolute Temperature

In this equation

$m$ is the mass of one molecule in kg

$v_{rms}$ is the root-mean-square speed of a molecule in m/s. You can think of this as the average speed of a molecule.

$k_B$ is the Boltzmann Constant. $k_B= 1.38\times 10^{-23}J/K$

$T$ is the absolute temperature of the gas in Kelvin

Example 16.4 – Average Speed Of Air Molecules

Air is roughly 80% Nitrogen and 20% Oxygen. Find the average speed (v_rms) of N₂ molecules in a room at 20.0°C.

Solution for (a)

The average speed of molecules is related to the temperature of the gas according to

$\frac{1}{2}mv_{rms}^2 = \frac{3}{2}k_B T$

We need to find m, the mass of one molecule of N₂.

Let’s look up Nitrogen in the periodic table

calculating the mass of one molecule of N₂:

mass of 1mol of N atoms = 14.0067g

mass of 1 mol of N₂ molecules = 28.0134g

mass of 6.02×10²³ molecules of N₂ = 28.0134g

mass of 1 molecule of N₂ = $\frac{28.0134g}{6.02 \times 10^{23}}=4.65 \times 10^{-23} g$

Mass must be in kg.

$4.65 \times 10^{-23} g \times \frac{1kg}{1000g}=4.65 \times 10^{-26}kg$

The temperature must be in Kelvin.

$T_K=T_C+273.15$

$T_K=20.0+273.15$

$T_K=293K$

Now we are ready to calculate v_rms for Nitrogen

$\frac{1}{2}mv_{rms}^2 = \frac{3}{2}k_B T$

$\frac{1}{2}(4.65 \times 10^{-26}kg) v_{rms}^2 = \frac{3}{2}(1.38\times 10^{-23}J/K)(293K)$

$v_{rms} =511m/s$

Attributions

This chapter contains material taken from Openstax College Physics-Temperature, Kinetic Energy, and the Gas Laws, and Openstax University Physics Volume 2, and is used under a CC BY 4.0 license. Download these books for free at Openstax

Information in the Human Body Temperature section is obtained from a Wikipedia entry on Thermoregulation.

To see what was changed, refer to the List of Changes.

Problems

[openstax univ. phys. vol. 2 – 1.45] Suppose a cold front blows into your locale and drops the temperature by 40.0 Fahrenheit degrees. How many degrees Celsius does the temperature decrease when it decreases by40.0ºF?
[openstax univ. phys. vol. 2 – 1.47(edited)]
1. At what temperature do the Fahrenheit and Celsius scales have the same numerical value?
2. At what temperature do the Fahrenheit and Kelvin scales have the same numerical value?
[openstax univ. phys. vol. 2 – 1.50] How much taller does the Eiffel Tower become at the end of a day when the temperature has increased by 15.0ºC Its original height is 321 m and you can assume it is made of steel.
[openstax univ. phys. vol. 2 – 1.57] Most cars have a coolant reservoir to catch radiator fluid that may overflow when the engine is hot. A radiator is made of copper and is filled to its 16.0-L capacity when at 10.0ºC. What volume of radiator fluid will overflow when the radiator and fluid reach a temperature of 95.0ºC given that the fluid’s volume coefficient of expansion is β=400×10^-6(1/ºC)? (Your answer will be a conservative estimate, as most car radiators have operating temperatures greater than95.0ºC).
[openstax univ. phys. vol. 2 – 2.18] The gauge pressure in your car tires is 2.50×10⁵Pa at a temperature of35.0ºC when you drive it onto a ship in Los Angeles to be sent to Alaska. What is their gauge pressure on a night in Alaska when their temperature has dropped to -40.0ºC? Assume the tires have not gained or lost any air.
[openstax univ. phys. vol. 2 – 2.19] Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of 20.0ºC. Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is 60.0ºC (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks.
A balloon filled with air has a volume of 0.200m³ and a pressure of 20.0psi at a temperature of 92.0°F.
1. What is the new volume if the balloon is placed in a refrigerator and cooled to 32.0°F and the pressure is reduced to 14.7psi?
2. How many moles of air are there in the balloon?
[openstax univ. phys. vol. 2 – 2.24] An airplane passenger has 100cm³ of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to7.50×10⁴ Pa?
[openstax univ. phys. vol. 2 – 2.27] An expensive vacuum system can achieve a pressure as low as 1.00×10^-7Pa at 20.0ºC How many molecules are there in a cubic centimeter at this pressure and temperature?
[openstax univ. phys. vol. 2 – 2.34] A car tire at a temperature of 25.0ºC contains 3.60 mol of gas in a 30.0-L volume.
1. What is the gauge pressure of air in this tire?
2. What will the gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and 25.0ºC? Assume the temperature remains at25.0ºC and the volume remains constant.
[openstax univ. phys. vol. 2 – 2.38] Some incandescent light bulbs are filled with argon gas. What is the v_rms for argon atoms near the filament, assuming their temperature is 2500 K?
[openstax univ. phys. vol. 2 – 2.42] What is the total translational kinetic energy of the air molecules in a room of volume 23.0m³ if the pressure is 9.50×10⁴Pa, and the temperature is 21.0ºC?
A nitrogen canister has a volume of 5.00L and contains gas at a pressure of 2200psi at 20.0°C.
1. Find the mass of nitrogen gas in the container.
2. What is the average kinetic energy per molecule?
3. What is the v_rms of the nitrogen molecules in this container?
Determine the density of CO₂ at a temperature of 75.0°F and a pressure of 0.950atm.
What is the molar mass of a gas if 0.0494 g of the gas occupies a volume of 0.100 L at a temperature 26 °C and a pressure of 5.94 psi?
A 2.00L cylinder contains laughing gas, N₂O, at a temperature of 30.0ºC and at atmospheric pressure
1. What is the mass of the gas in this container?
2. What is the v_rms of the N₂O molecules?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

temperature and the zeroth law of thermodynamics

THE ZEROTH LAW OF THERMODYNAMICS

temperature scales

thermal expansion of solids and liquids

ideal gas law

kinetic theory – relating pressure and temperature to molecular motion

Section summary

Attributions

Problems

License

Share This Book