Unit 11 – Potential Energy and Energy Conservation

Beta Keramati

Work and Energy

Last Update: 12/05/2022

Conservative forces and Potential energy

As we saw in UNIT 10, negative work done by a force removes kinetic energy from a system.

$W_{net}=\Delta KE$

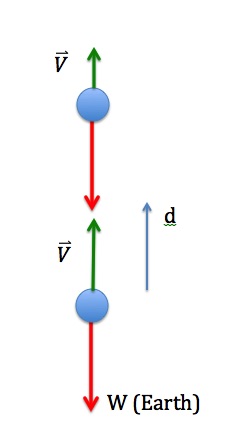
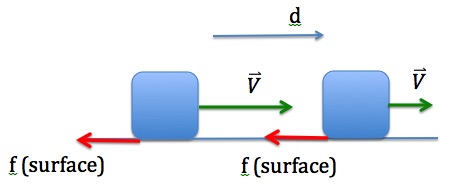
For example, a ball that is thrown upward, slows down due to the gravitational force. This means that the negative work done by the gravitational force reduces the kinetic energy of the ball. Similarly, if you push a block on a table and let go, the block slows down due to friction. In other words, the negative work done by the friction force reduces the kinetic energy of the block.

Fig11.1 – Ball losing kinetic energy as it moves upward. Gravitational force does negative work on the ball.

Figure 11.2 – Block loses kinetic energy as it slides on the table. Friction force does negative work on the block.

Even though both forces do negative work, there is a fundamental difference between these two situations. The ball eventually turns around and comes back down, and while it is moving down the gravitational force does positive work and the kinetic energy goes back up again. The block, on the other hand, simply stops. In the case of the ball, the kinetic energy that was removed from the system by the negative work done by the gravitational force, remains retrievable. All the kinetic energy that was removed while the ball was moving up can be put back into the system again while the ball comes back down. That’s not the case for the block. The kinetic energy that was removed from the system by the negative work done by the friction force is no longer retrievable. This kinetic energy has been permanently removed from the system.

When the gravitational force does negative work and removes kinetic energy from a system, that energy is still within the system and can be retrieved and converted back into kinetic energy again. This “stored” energy is called potential energy. So there is a potential energy associated with the gravitational force but not with friction force.

In general, forces that have a potential energy associated with them are called conservative forces. Negative work done by a conservative force reduces the kinetic energy of the system but increases the potential energy, while positive work done by a conservative force reduces the potential energy and puts that energy back into the system in the form of kinetic energy.

Another characteristics of a conservative force is that when the force does work over a closed path, the total work is zero. The following two examples demonstrate this point.

Example 11.1

You lift an oversized library book, weighing 20 N, 1.0 m vertically down from a shelf, and carry it 3.0 m horizontally to a table. When you’re finished, you move the book in a straight line back to its original place on the shelf. How much work does the gravitational force do on the book throughout the whole process?

Solution

Work done by a constant force is $W=FdCos\theta$ .

To find work done along path (b) we need to find the angle between the gravitational force and the line BA. This angle is 90°+Θ.

$Tan \theta = \frac{1.0m}{3.0m}$

$\theta = 18.4^\circ$

The distance from B to A is

$d=\sqrt{(1.0m)^2 + (3.0m)^2}$

$d=3.16m$

The total work done by the gravitational force along path (a) and (b) is

$W=(20N)(1.0m)Cos(0^\circ)+(20N)(3.0m)Cos(90^\circ)+ (20N)(3.16m)Cos(90^\circ +18.4^\circ)$

$W=0J$

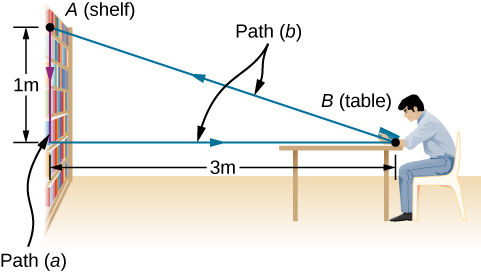
Discussion

Gravitational force is a conservative force. The work done by any conservative force over any closed path is always zero.

Example 11.2 – Moving a Couch

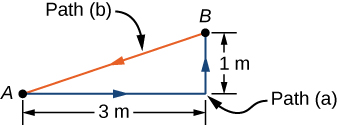
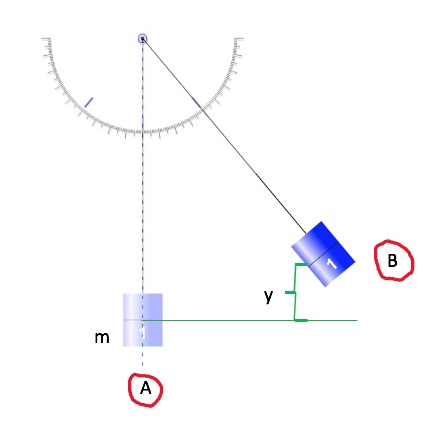
You decide to move your couch to a new position on your horizontal living room floor. The mass of the couch is 102kg and the coefficient of kinetic friction between the couch and the floor is 0.600. (a) You first push the couch 3.00 m parallel to a wall and then 1.00 m perpendicular to the wall (A to B in Figure 11.5). But you don’t like the new position, so you move the couch straight back to its original position (B to A in Figure 11.5). What was the total work done by the friction force in this whole process?

Figure 11.6 – Free Body Diagram of the couch

Solution

Work done by a constant force is $W=FdCos\theta$ .

Since the friction force is $f_k=\mu_k N$ , to find the friction force, we first need to calculate the normal force. This means we have to apply Newton’s Second Law.

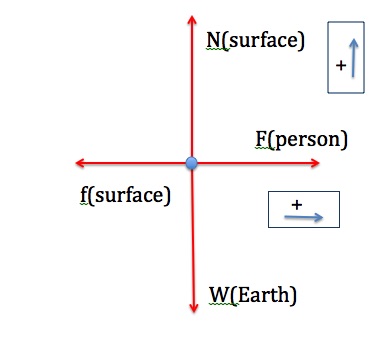
The free body diagram for the couch is represented in Figure 11.6. the x and y axes are horizontal and vertical and the positive directions are marked on the diagram. Applying Newton’s Second Law in the y-direction yields

$a_y =\frac{\sum F_y}{m}$

$0 =\frac{N - (102kg)(9.8m/s^2)}{102kg}$

$N = 1.00 \times 10^3 N$

Now we can calculate the friction force.

$f_k=\mu_k N$

$f_k=(0.600)(1.0 \times 10^3 )N$

$f_k=600 N$

To find the work done from B to A we need to find the length of this path.

$d=\sqrt{(1.0m)^2 + (3.0m)^2}$

$d=3.16m$

Since the friction force always points in the opposite direction of motion, the angle between the friction force and the displacement is 180°.

The total work done by the friction force in this process is

$W=FdCos\theta$

$W=(600N)(3.00m)Cos(180^\circ) +(600N)(1.00m)Cos(180^\circ) +(600N)(3.16m)Cos(180^\circ)$

$W=-4300J$

Discussion

Friction is a non-conservative force. The work done by a non-conservative force over a closed path is not zero.

The fact that the work done by a conservative force over a closed path is zero implies that the amount of work done by a conservative force does not depend on the shape of the path. As long as the initial position (point A) and the final position (point B) remain the same, the amount of work done by a conservative force from A to B is the same no matter what path is taken.

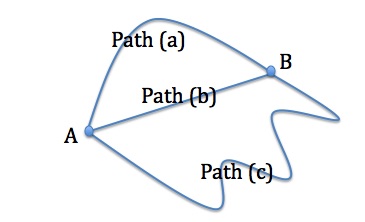
Figure 11.7 – work done by a conservative force is independent of the path

Conservation of mechanical energy

As it was mentioned in the previous section, the kinetic energy that is removed from a system by negative work done by a conservative force is stored in the system in the form of potential energy. This means that work done by a conservative force is the negative of the change in potential energy – negative work by a conservative force increases the potential energy, while positive work decreases it. This can be expressed in the form of this equation

$\boxed{W_{cf}=-\Delta U}$ Work By a Conservative Force

where W_cf represents work done by a conservative force, and U represents potential energy.

Let’s combine this with work-energy theorem

$W_{net}=\Delta KE$

W_net is work done by all forces. In general, some of the forces are conservative and some are not. So we can think of W_net as W_cf + W_ncf. (W_ncf stands for work done by non-conservative forces). Therefore we can do the following substitutions

$W_{net}=\Delta KE$

$W_{cf} + W_{ncf}=\Delta KE$

$-\Delta U+ W_{ncf}=\Delta KE$

$W_{ncf}=\Delta KE + \Delta U$

So the fundamental work-energy theorem can be expressed with either one of the following equations

$W_{net}=\Delta KE$ is the same as $W_{ncf}=\Delta KE + \Delta U$

Now let’s examine the consequences of W_ncf = 0 . This could happen either because there may not be any non-conservative forces acting on an object, or the non-conservative forces may not be doing any work during a certain process.

If $W_{ncf}=0$ Then $\Delta KE + \Delta U=0$

$\Delta KE + \Delta U=0$ means the sum of potential energy and kinetic energy does not change throughout the process, or that U+KE remains constant. The sum of potential and kinetic energy in a system is called mechanical energy. In physics, when a quantity stays constant during a process, we say that quantity is “conserved”. Therefore, when W_ncf=0 the mechanical energy of the system is conserved.

$\Delta KE + \Delta U=0$ can also be expressed in terms of the initial and final energies.

$\Delta KE + \Delta U=0$

$(KE_f -KE_i) +(U_f - U_i)=0$

$KE_i+U_i =KE_f + U_f$

When $W_{nc}\ne 0$ , the mechanical energy of the system changes, but the overall energy of the system is still conserved. The overall energy includes thermal energy, chemical energy, sound energy, etc. For example, friction is a non-conservative force. When friction does negative work, kinetic energy of the system goes down but the thermal energy of the system may go up. The important thing to note is that this thermal energy cannot be converted back into kinetic energy. So the kinetic energy that was removed by the non conservative force is permanently gone and the mechanical energy is permanently reduced even though the overall energy of the system hasn’t changed.

Gravitational and elastic potential energy

Gravitational Potential energy

The potential energy associated with work done by the gravitational force is called gravitational potential energy, U_{gravitational}. In this section we will derive an expression for calculating this energy.

$W_{grav}=-\Delta U_{grav}$

Since the gravitational force is always downward (toward the center of the Earth), the gravitational force does work only when the displacement has a vertical component (the object’s position changes in the vertical direction). Also, since the gravitational force is conservative, the amount work is independent of the path. In Figure 11.8, it doesn’t matter which path the object of mass m takes to go from A to B , the work done by the gravitational force along any path from A to B is

work done by a constant force: $W=FdCos\theta$

$W_{grav}=(mg)(y_2 - y_1)Cos(180^\circ)$

$W_{grav}=-mg(y_2 - y_1)$

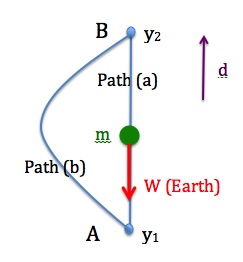
The work done by the gravitational force changes the gravitational potential energy. Therefore

$W_{grav}=-\Delta U_{grav}$

$W_{grav}=-mg(y_2 - y_1)$

$\Delta U_{grav}=mg(y_2 - y_1)$

Notice that what matters is the change in the potential energy. In other words, the actual vertical position of the object is irrelevant. What matters is the vertical displacement from start to finish. As long the vertical displacement is the same, the same amount of gravitational potential energy changes and the same amount of work is done by the gravitational force. Moving a book from a table to a shelf 1m above the table changes the gravitational potential energy by the same amount as moving the same book from that shelf to another shelf that is 1m higher up.

Putting it all together we get

$\boxed{U_{grav}=mgy}$ Gravitational Potential Energy

Where y is the vertical position relative to a point where we arbitrarily set y=0.

Note that the gravitational potential energy is associated with the gravitational force, and the gravitational force is due to the interaction between the Earth and the object. We just found that a change in the distance between the object and the center of the Earth changes the gravitational potential energy. So the gravitational potential energy is an energy that belongs to the system of Earth and object.

The following simulation shows the transformation between the gravitational potential energy and the kinetic energy for a skater on a frictionless track. Notice that as the skater descends her gravitational potential energy (blue curve) goes down while her kinetic energy (green curve) goes up. The reverse happens when she ascends. The whole time the total energy (yellowish curve) which is the sum of the kinetic and gravitational potential energy stays constant.

elastic potential energy

There are many conservative forces, besides the gravitational force. But for now, we will consider only one other conservative force – force applied by a spring (or anything that behaves like a spring) or elastic force. As we saw in UNIT 8, when a spring is stretched or compressed, the spring applies a force that is given by the Hooke’s Law as $F_{spring}=-kx$

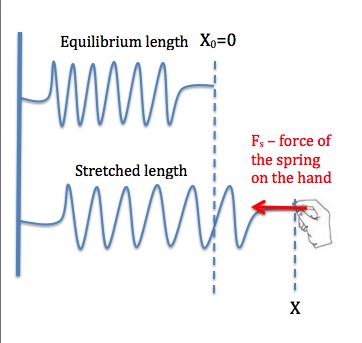
Force of the spring is clearly not a constant force because it varies with the length of the spring. Therefore we cannot use $W=FdCos\theta$ to calculate work done by this force. But we can plot this force versus displacement of the spring, x, and determine the area under the curve to find work. This method was mentioned in Unit 10 where calculating work was first introduced.

The graph of F_spring =-Kx vs x is a straight line with a slope=-K

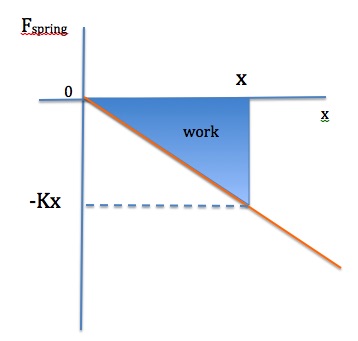
Work done by the spring as the length of spring changes from 0 to x is the area of the triangle.

$Work_{F_s}=\frac{1}{2}(-Kx)(x)$

$Work_{F_s}=-\frac{1}{2}Kx^2$

Since the spring force is a conservative force, there is a potential energy associated with it. This potential energy is called elastic potential energy. The work done by the force of the spring changes the elastic potential energy of the system. As we saw in the previous section,

$W_{cf}=-\Delta U$

Applying this for the spring we get

$W_{F_s}=-\Delta U_{elastic}$

$-\frac{1}{2}Kx^2=-\Delta U_{elastic}$

If we set the elastic potential energy to be zero where the spring is at its equilibrium length and x=0, we get

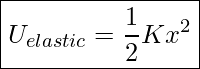$\boxed{U_{elastic} =\frac{1}{2}Kx^2}$ Elastic Potential Energy

where x represents how far the spring has been compressed or stretched relative to its equilibrium length.

The following simulation shows how elastic potential energy changes when the spring is stretched and compressed. It also shows the effect of changing the spring constant on potential energy.

Summary of the relationships between work and energy

$W_{net}=\Delta KE$ is the same as $W_{ncf}=\Delta KE + \Delta U$

If $W_{ncf}=0$ Then $\Delta KE + \Delta U=0$

$\Delta KE + \Delta U=0$ is the same as $KE_i+U_i =KE_f + U_f$

$KE =\frac{1}{2}mv^2$

$U_{grav}=mgy$

$U_{elastic} =\frac{1}{2}Kx^2$

qualitative Examples

Swinging Pendulum

When a pendulum swings, the system has kinetic energy and gravitational potential energy. At the bottom of the swing at point A, all the energy is kinetic (1/2 mv²), and when it is at the top of the swing at point B, all the energy is gravitational potential energy (mgy), and when it is somewhere between A and B, some of the energy is kinetic and some of it is potential.

In the absence of friction, the total energy of the system stays constant, and the mechanical energy is conserved. Without friction, the pendulum keeps swinging forever.

If there is friction, then the mechanical energy gets gradually converted to thermal energy and the pendulum eventually stops.

Look at the change in kinetic and potential energy that are shown on the left hand side, in the simulation below. Notice how, in the absence of friction, the total energy is the sum of kinetic and potential energy. The simulation first runs at normal speed and then it is slowed down so that you can observe the change in energy. Finally, you can see the effect of friction on the total energy of this system. When friction is present, the mechanical energy is gradually dissipated and converted into thermal energy. The oscillation stops when all the mechanical energy is gone.

Oscillating Mass – Spring System

In the following simulation, a mass is attached to a vertical spring and when the mass is pulled down and released, the system oscillates up and down. Since y=0 is set at the floor, the mass always has some gravitational potential energy. When the mass passes the point that marks the equilibrium position of the mass-spring system, the mass is moving the fastest and has its maximum kinetic energy. When the mass is farthest away from the equilibrium point, the elastic potential energy is at its maximum and there is no kinetic energy (that’s where the direction of motion changes). In other words, as the system oscillates, kinetic energy is converted to elastic potential energy and vice versa. In the absence of friction, the total energy of the system is constant. This means the mechanical energy is conserved. The relative amount of elastic potential, gravitational potential, kinetic, thermal, and total energies are shown on the left. The simulation runs first at normal speed with no damping force (friction force). Then the simulation is slowed down so that you can observe the exchange of energy during one oscillation. Notice that in absence of friction, the total energy does not change. Then the simulation goes back to normal speed and damping force is added. Notice that damping reduces the mechanical energy of the system and when all of it is converted to thermal energy, oscillations stop.

Skate Park

The next simulation shows a skater on a track. At first, there is no friction and the energy graphs show kinetic energy getting converted to gravitational potential energy and vice versa while the total energy stays constant. The simulation is slowed down so that you can observe the change in the kinetic and potential energy. When friction is added, the mechanical energy is gradually reduced and converted to thermal energy. When all the mechanical energy is gone, the skater stops.

problem solving strategy and example problems

Since work is the process of adding or removing energy from a system, to use the work-energy theorem in solving problems we need to first identify the system of interest, its initial state, and its final state. Next, identify the forces that do work on the system as the system goes from its initial state to its final state. Decide whether each force is conservative or non-conservative. Finally, apply the work-energy theorem, replacing work done by conservative forces with the change in their associated potential energy, and do the algebra to solve the problem. The following examples demonstrate this approach.

Example 11.3

A 60.0-kg person jumps onto the floor from a height of 3.00 m. If he lands stiffly with his knee joints compressing by 0.500 cm, calculate the force on the knee joints.

Solution

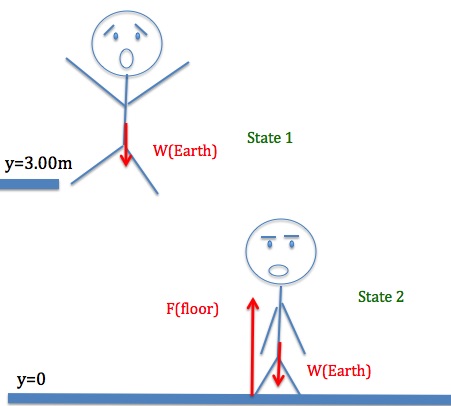
Figure 11.11 shows the system in state 1(the instant the person steps off the platform, v=0) and state 2 (the instant the force applied by the floor compresses his knee joints and brings him to a stop v=0). We apply the work-energy theorem for the process of going from state 1 to state 2.

The force applied by the floor is a non-conservative force. This upward force must do work to stop the person’s downward motion. This work is done on the knee joints. So the angle between force F and displacement of the knee joints is 180°. The kinetic energy at state 1 and kinetic energy at state 2 are both zero. The only potential energy that changes in this process is the gravitational potential energy.

$State(1)$ $\Rightarrow$ $State(2)$

$W_{ncf}=\Delta KE + \Delta U$

$W_F=0 + (mgy_2 -mgy_1)$

$F(0.500 \times 10^{-2}m)Cos(180^\circ)=0 + (60.0kg)(9.8m/s^2)(0) -(60.0kg)(9.8m/s^2)(3.00m))$

$F=3.53 \times 10^5 N$

Discussion

Such a large force (500 times more than the person’s weight) over the short impact time is enough to break bones. A much better way to cushion the shock is by bending the legs. A bending motion of 0.5 m this way yields a force 100 times smaller than in the example.

Video Example – Skier’s speed at the bottom of the ramp

Example 11.4

Consider the roller coaster shown in Figure 11.12. Assume negligible friction.

a) What is the final speed of the roller coaster if it starts from rest at the top of the 20.0 m hill?

(b) What is its final speed if its initial speed is 15 m/s?

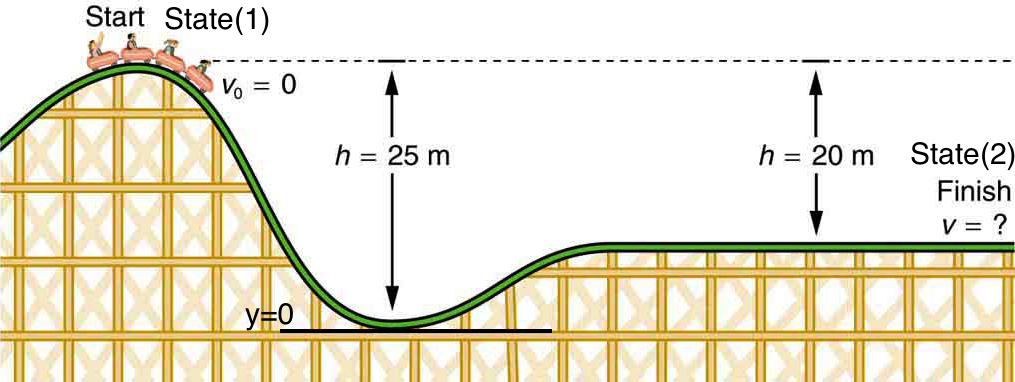
Solution for (a)

As the roller coaster goes from the state(1) to state(2) the forces acting on it are the gravitational force and the normal force applied by the track. Let’s take y=0 at the bottom of the lowest hill and apply the work-energy theorem to this process.

$State(1)$ $\Rightarrow$ $State(2)$

$W_{ncf}=\Delta KE + \Delta U$

Since the normal force is always perpendicular to the displacement of the roller coaster, it does not do any work. Therefore, there is no work done by non-conservative forces and the mechanical energy of the system is conserved.

$KE_1+U_1 =KE_2 + U_2$

$\frac{1}{2}mv_1^2+mgy_1 =\frac{1}{2}mv_2^2+ mgy_2$

$0+m(9.8m/s^2)(25m) =\frac{1}{2}mv_2^2 + m(9.8m/s^2)(20m)$

$v_2=9.9m/s$

Solution for (b)

The approach is the same as (a), except that the KE at state 1 is not zero this time.

$State(1)$ $\Rightarrow$ $State(2)$

$KE_1+U_1 =KE_2 + U_2$

$\frac{1}{2}m(15m/s)^2+m(9.8m/s^2)(25m) =\frac{1}{2}mv_2^2 + m(9.8m/s^2)(20m)$

$v_2=18m/s$

Video Example – Moving up a ramp when there is friction

Example11.5

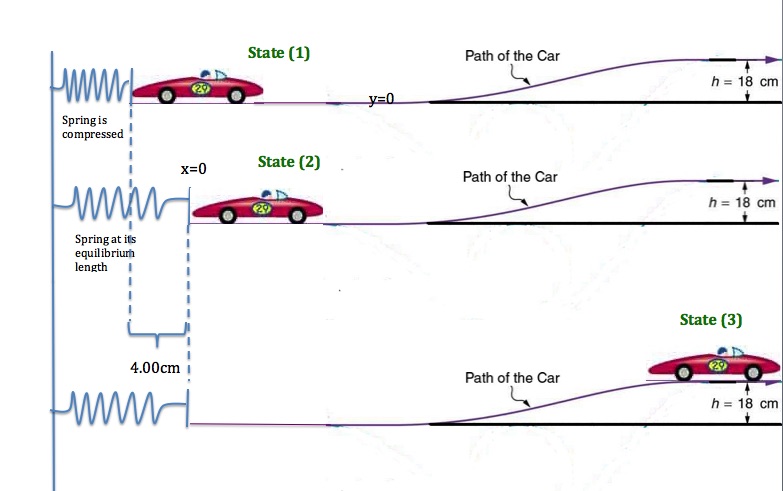
A 0.100-kg toy car is propelled by a compressed spring with a spring constant of 250N, as shown in Figure 11.13. The car follows a track that rises 0.180 m above the starting point. The spring is initially compressed 4.00 cm. Assume friction force is negligible.

a) How fast is the car moving before it starts up the slope?

b) How fast is it moving at the top of the slope?

c) How much work is done by the friction force on the car if speed at the top of the slope is one half of what you found in (b)?

Solution for (a)

Since there is no friction force to slow down the car, the speed of the car at the instant it leaves the spring, state(2), is the same as its speed when it reaches the slope. To find the speed at state(2), we apply the work-energy theorem for the process of going from the state(1) to state(2).

The forces acting on the car from state(1) to state(2) are the gravitational force, the spring force, and the normal force of the ground. The gravitational and normal forces are perpendicular to the displacement and they don’t do any work. Therefore, there is no non-conservative force doing work on the car and mechanical energy is conserved. Notice that at state(1), v=0, and at state(2), the spring is at its equilibrium length.

Applying the work-energy theorem from yields

$State(1)$ $\Rightarrow$ $State(2)$

$KE_1+U_1 =KE_2 + U_2$

$\frac{1}{2}mv_1^2 + \frac{1}{2}Kx_1^2 =\frac{1}{2}mv_2^2 + \frac{1}{2}Kx_2^2$

$0+\frac{1}{2}(250N/m)(4.00 \times 10^{-2})^2 =\frac{1}{2}(0.100kg)v_2^2 + 0$

$v_2=2.00m/s$

Solution for (b)

There are two ways to determine the speed at the top of the hill. We can apply the work-energy theorem from the state(2) to state(3), or we can apply it for going from the state(1) to state(3) directly. We will do it both ways. Either way, there is no work done by non-conservative forces and the mechanical energy is conserved.

$State(2)$ $\Rightarrow$ $State(3)$

$KE_1+U_1 =KE_2 + U_2$

$\frac{1}{2}mv_2^2 + mgy_2 =\frac{1}{2}mv_3^2 + mgy_3$

$\frac{1}{2}(0.100kg)(2.00m/s)^2+0=\frac{1}{2}(0.100kg)v_3^2 + (0.100kg)(9.8m/s^2)(0.180m)$

$v_3=0.687m/s$

Now let’s go from state(1) to state(3)

$State(1)$ $\Rightarrow$ $State(3)$

$KE_1+U_1 =KE_2 + U_2$

$\frac{1}{2}mv_1^2 + mgy_1 + \frac{1}{2}Kx_1^2=\frac{1}{2}mv_3^2 + mgy_3 + \frac{1}{2}Kx_3^2$

$0 +0+ \frac{1}{2}(250N/m)(0.0400m)^2 =\frac{1}{2}(0.100kg)v_3^2 + (0.100kg)(9.8m/s^2)(0.180m)+0$

$v_3=0.687m/s$

Discussion for (a) and (b)

In state(1) all the energy of the system is in the form of elastic potential energy. As the system goes from the state(1) to state(2), this potential energy is converted into kinetic energy. From state(2) to state(3), the kinetic energy is partially converted into gravitational potential energy. So the system has various types of energy at different states, but the total energy of the system remains constant the whole time – at all states and while it is transitioning from one state to another state.

Solution for (c)

Since the friction force acts on the car throughout the whole path, we can no longer determine the speed of the car at state(2). The only way to find the work done by the friction force is to apply the work-energy theorem from the state (1) to state(3). Friction, of course, is a non-conservative force and the mechanical energy of the system is no longer conserved. If v₃ =0.344m/s

$State(1)$ $\Rightarrow$ $State(3)$

$W_{ncf}=\Delta KE + \Delta U$

$W_f=(\frac{1}{2}mv_3^2 - \frac{1}{2}mv_1^2) +(\frac{1}{2}Kx_3^2 - \frac{1}{2}Kx_1^2) + (mgy_3 - mgy_1)$

$W_f=[\frac{1}{2}(0.100kg)(0.344m/s)^2 - 0] +[0 - \frac{1}{2}(250N/m)(0.0400m)^2] + [(0.100kg)(9.8m/s^2)(0.180m) - 0]$

$W_f=-4.82J$

Discussion for (c)

This means 4.82J of mechanical energy is dissipated due to friction. This energy was removed from the system due to work done by friction force and can no longer be converted into mechanical energy.

Video Example – Block striking a spring on a horizontal rough surface

Video Example – Person jumping on a trampoline

Attributions

This chapter contains material taken from Openstax College Physics-Work, Energy, and Energy Resources, and Openstax University Physics Volume 1 – Work and Kinetic Energy, Potential Energy and Conservation of Energy, and is used under a CC BY 4.0 license, . Download these books for free at Openstax

The Elastic Potential Energy simulation is a screencast of Hooke’s Law – Phet Simulation.

The Energy Of A Pendulum simulation is a screencast of Pendulum Lab – Phet Simulation.

The Energy Of A Mass-Spring System simulation is a screencast of Masses and Springs – Phet Simulation.

The Energy Of A Skater simulation is a screencast of Energy Skate Park – Phet Simulation.

To see what was changed, refer to the List of Changes.

problems

[openstax univ. phys. vol. 1 – 8.31] A boy throws a ball of mass 0.250kg straight upward with an initial speed of 20.0m/s. When the ball returns to the boy, its speed is 17.0m/s. How much much work does air resistance do on the ball during its flight?
[openstax univ. phys. vol. 1 – 8.37] Assume that the force of a bow on an arrow behaves like the spring force. In aiming the arrow, an archer pulls the bow back 50.0 cm and holds it in position with a force of 150N. If the mass of the arrow is 50.0g and the “spring” is massless, what is the speed of the arrow immediately after it leaves the bow?
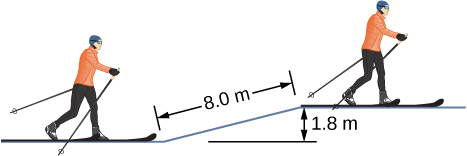
[openstax univ. phys. vol. 1 – 8.38] A 100kg man is skiing across the level ground at a speed of 8.00m/s when he comes to the small slope 1.80 m higher than the ground level shown in the following figure.
1. If the skier coasts up the hill, what is his speed when he reaches the top plateau? Assume friction between the snow and skis is negligible.
2. What is his speed when he reaches the upper level if an 80.0N frictional force acts on the skis?
Consider the 200g block starting from rest at point A as shown below.
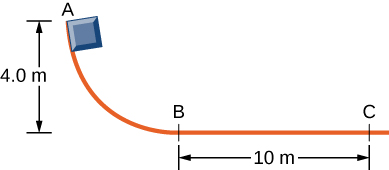
1. Find the speed of the block at point C if the track is frictionless.
2. Assume A to B is frictionless, but there is enough friction from B to C to bring the block to a stop at point C. Find the coefficient of kinetic friction between the block and the track from B to C.
3. Assume there is friction from A to B, but B to C is frictionless. How much work is done by the friction force from A to B if the block’s speed is 8.00m/s at C?
[openstax univ. phys. vol. 1 – 8.42-modified] A small block of mass 500g slides without friction around the loop-the-loop track with a radius R=25.0cm as shown below.
1. If the block starts from rest at A, what is its speed at B?
2. What is the force of the track on the block at B?
[openstax univ. phys. vol. 1 – 8.89-modified]A box slides on a frictionless surface with a total energy of 50.0J. It hits a spring and compresses the spring a distance of 25.0 cm from equilibrium.
1. Find the spring constant of the spring.
2. If the same box with the same initial energy slides on a rough surface, it only compresses the spring a distance of 15.0 cm. How much energy is dissipated due to friction?
The spring of a spring gun has a spring constant k=850N/m. When the gun is aimed vertically, a 70.0g ball is shot to a height of h=1.50 m above the end of the expanded spring as shown.
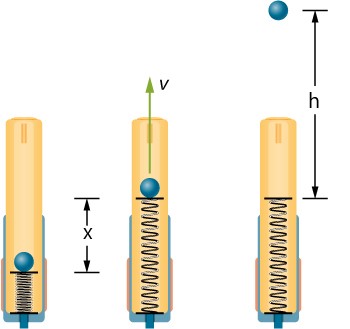
1. How much was the spring compressed initially?
2. What is the speed of the ball at the moment it leaves the spring?
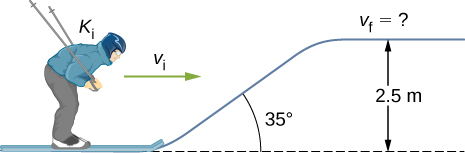
[openstax unv. phys. vol. 1 – 8.60] A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-m high rise as shown. Find her final speed at the top, given that the coefficient of friction between her skis and the snow is 0.800.
A block of mass 300g is released from rest from a height of 2.00m on top of a ramp inclined at 30.0°. The block slides down and eventually comes to rest after compressing a horizontal spring placed at the bottom of the ramp as shown. The spring has a spring constant of 525N/m, and the distance from the bottom of the incline, point B, and the spring, point C, is 80.0cm.
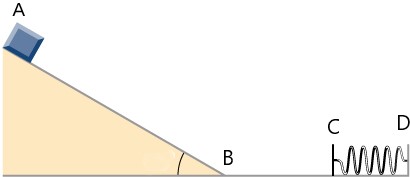
1. If all surfaces are frictionless, how much does the block compress the spring?
2. If the ramp is frictionless but the coefficient of kinetic friction between the block and the entire horizontal surface, from B to D is 0.120, how much does the block compress the spring?