We have already seen that present value of a perpetuity can be described by the formula: P₀ = CF ÷ i. We have also provided both the algebraic derivation of this formula and a discussion as to how the present value of a perpetuity approaches (but never quite reaches) the price described by the formula.

Still, many students find the idea of limits – and of the infinitesimal – difficult to grasp.  Our intent here is to further elucidate the notion that present values decrease over time with the result that distant cash flows become so small, so infinitesimal – they have so many decimal places – that they add virtually nothing to the aggregate present value. In making this observation, you will also note that, as a result, the cumulative value of the perpetuity’s present value approaches the theoretical price described by the formula, as posited by mathematicians. This is as it should be.

Let us say that a perpetuity’s cash flows are $1 and the interest rate at which we shall discount the series is 10%. The present value therefore would be: P₀ = $1 ÷ .10 = $10.  This is confirmed in the table below.

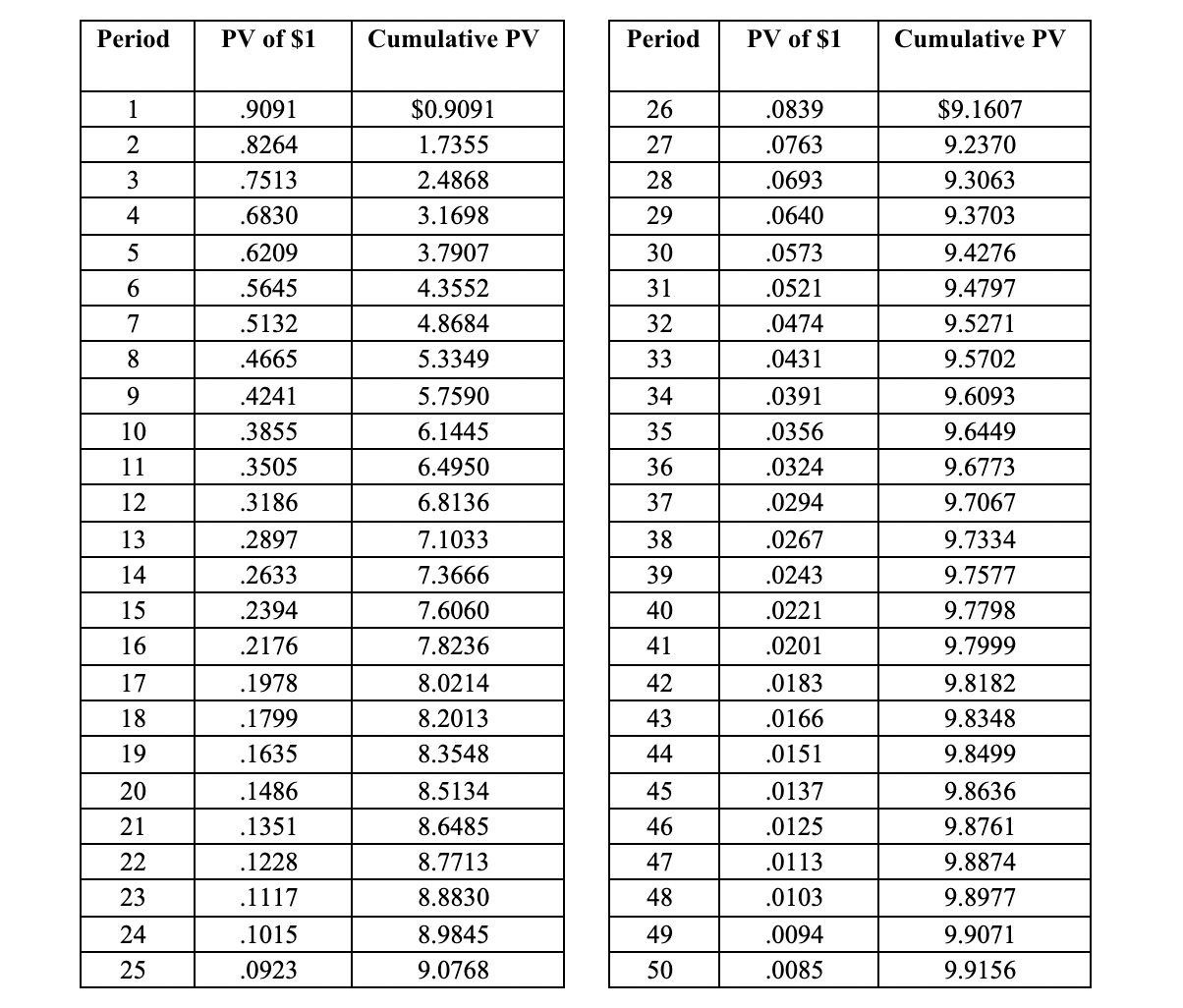
After 25 years, we reach 90% of the aforecited aggregate present value, and by the 50th year, we exceed 99% of the $10 value. With the passage of more time, we shall get closer and closer to $10, but only reach $10 in infinite space.