10.12 Interpolation Illustrated
Interpolation may be useful in order to estimate future (and present-) values when one does not wish, or have the ability, to calculate more precise measures. The reason for the error has to do with the curvilinear relationship between (discount- and) compound interest rates and their related multipliers. This is best seen by illustration.
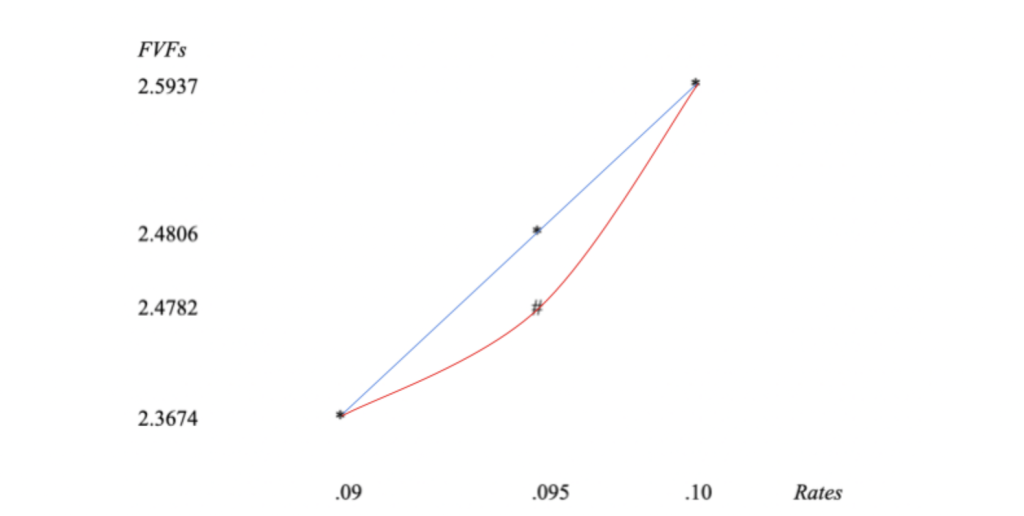
One may readily see that, by connecting the asterisks, the interpolated value of 2.4806 resides on a straight line between the correctly calculated future value multipliers for 9% and 10% respectively.
However, the time value of money is not linear. Any time an exponent is involved, you will not get a linear relationship, but a curvilinear outcome of some sort. Hence, the correct multiplier for 9.5% is 2.4782, which is lower than the interpolated arithmetic average of 2.4806. If one joins the asterisks for 9% and 10% to the mathematically calculated middle value of 2.4782 (represented by “#”), one readily observes the curvilinear relationship between compound interest rates and their respective multipliers. In short, as rates increase, future values increase in non-linear fashion. Correspondingly, present values would decrease non-linearly. The non-linear nature of these curves will soon be discussed in greater depth when we get to “Volatility.” Basic mathematical examples will be presented.
