10.2 The Time Value of Money and Interest
For each of the following questions, assume you have $1 and that interest on it will be paid in full, at the END of the stated period. What are the future values (FVs) given each of the following questions? In other words, how much money will you have at the relevant future points in time? (If you had more than $1, the answers would be the appropriate multiple thereof.)
As we go through the questions and calculations, observe how the outcomes, or solutions, change. Try to explain the reasons for the differences in the outcomes. Also, observe that the seemingly small differences in outcomes are really not as trivial as may seem at first glance. We are illustrating Future Values, in each question, of just one dollar of money that we have now – of Present Value. Suppose we were instead dealing with millions of dollars?
As we go through each question, we will, methodically and painstakingly, create a general symbolic formula, which may be employed for any similar problem. Insert the appropriate values into the formulae to solve the problems numerically. (Solutions follow.)
1. You will earn 5% interest, paid once a year, at the END of the year, for one year.
You have $1 now of Present Value (PV). In one year, you will receive your “principal” of $1 back plus interest at an annual rate of return (R) of 5%. A general Future Value (FV) formula will therefore be:
FV = PV (1 + R)
Insert the relevant data into the formula in order to solve for the Future Value.
As we go through this analysis, you will need to learn and remember the symbols or abbreviations.
2. Same as question #1, but R = 10%.
Here we will use the same formula as above, but you will insert a different rate for R. What is the Future Value? Why is the outcome different?
3. Same as question #2, i.e., R = 10%, but for two years (n years), rather than just one.
We will now have two years of compound interest; n = 2. Therefore, we apply the FV formula, slightly modified, a second time:
FV = PV (1 + R) (1 + R)
FV = PV (1 + R)n
Here, the exponent, “n,” stands for the number of years in which the money compounds.Once again, in this case, n = 2. What is the Future Value? Why is the outcome different than in the prior question?
4. 10% interest, twice a year, for one year.
Interest is always quoted as an annual rate, unless explicitly noted otherwise.
Our annual rate is still 10%, but we will receive half of it, i.e., R ÷ p = 0.10 ÷ 2 = 0.05, at the end of each half-year. The letter, “p” stands for the number of compounding periods per year; here p = 2.
FV = PV (1 + R/p)(1 + R/p)
Notice that, while n = 2, there are now two compounding periods per year, so the exponent must reflect that. Our exponent is therefore now: “n × p.”
Whenever p ≠ 1, we must make two adjustments to the formula: “R/p” in the rate part of the formula and “n × p” in the exponent. While in theory P can take on any integer value, it will actually be equal to 1, 2, 4, 12, or 365 for annually, semi-annually, quarterly, monthly, or daily respectively. (In this example, n = 1; when p = 1, we tend to leave it out as the power of one is implicit.) Our general formula now becomes:
FV = PV (1 + R/p)n × p
Our Future Value formula is now complete. What Future Value do you get? Why is the outcome different than in question #2?
Note that, when solving for Future Value, we multiply the Present Value by a “factor” of (1 + R/p) n × p. A factor is simply a multiplier. This multiplicative and exponential process is referred to as compounding.
5. Same as question #4, but for two years.
We can employ the formula in the prior question. Remember, “p” occurs twice in our formula. Here, n = 2, and p = 2. What is your Future Value? Why is the outcome different than in question #3?
6. What happens to future values as interest rates (“R”), the number of years (“n”), and compounding frequency (“p”) increase? In answer to this question, we present, in summary, the “Three Commandments” of the Time Value of Money.
The Three Commandments of TVM
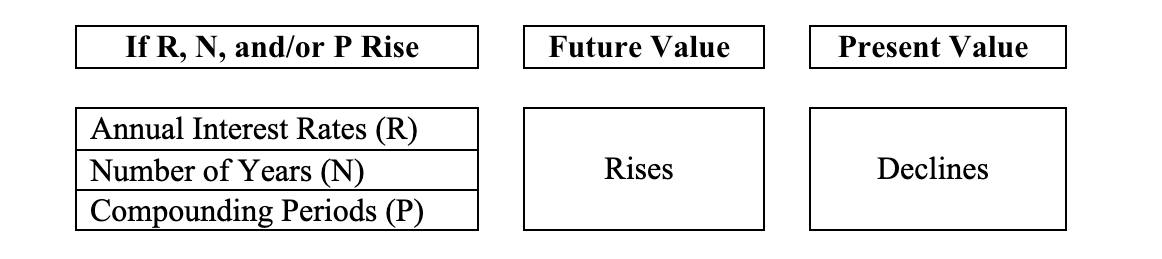
Of course, the opposite will occur if R, N, and/or P decline. Below, we explain Present Values.
7. For each of the above questions, what would be the present value of $1 to be received at the end of the stated periods? In other words, where in questions 1 though 5, we assumed $1 of PV and had to calculate its FV, we will now assume $1 of FV and calculated its PV using the data in each of the first 5 questions. Here, we will re-employ our Future Value formula, but transpose the FV and PV numbers so that we can solve for PV, rather than for FV.
PV = FV ÷ (1 + R/p)n × p
Thus, when solving for Present Value we divide the Future Value by the (1 + R/p) n × p factor. This division process is referred to as discounting.
Rather than dividing, we can also multiply the Future Value by the reciprocal of the divisor.
PV = FV × [1 ÷ (1 + R/p)n × p]
Definition: A reciprocal is the inverse of a number, which is arrived at by turning the number upside down! So, 1/2 or 0.5 is the reciprocal of 2. The reciprocal of 5 is 1/5 – or 20%. So, (1 + R/p) n × p and [1 ÷ (1 + R/p) n × p] are reciprocals of one another.
In using Interest Rate Tables (soon), which display ready-made, already-calculated factors, you will note that all the factors’ values are stated as multipliers, including the Present Value Factors (PVFs). We will use tables in order to cut down on the number of calculations that we must make and to thereby reduce errors.
8. Is it a realistic question to ask what the PV is? How might this actually occur?
Of course it is! We will often know the future payments and wish to figure out the PVs! For example, you may wish to put aside some money for the down payment on a house in “n” years. Assuming you know the “discount rate,” how much must you set aside today in order to fund that amount? How much will you need to set aside today to fund your newborn child’s college tuition? A bond pays interest every six months in a known amount. How much should you pay today in order to receive those future amounts?
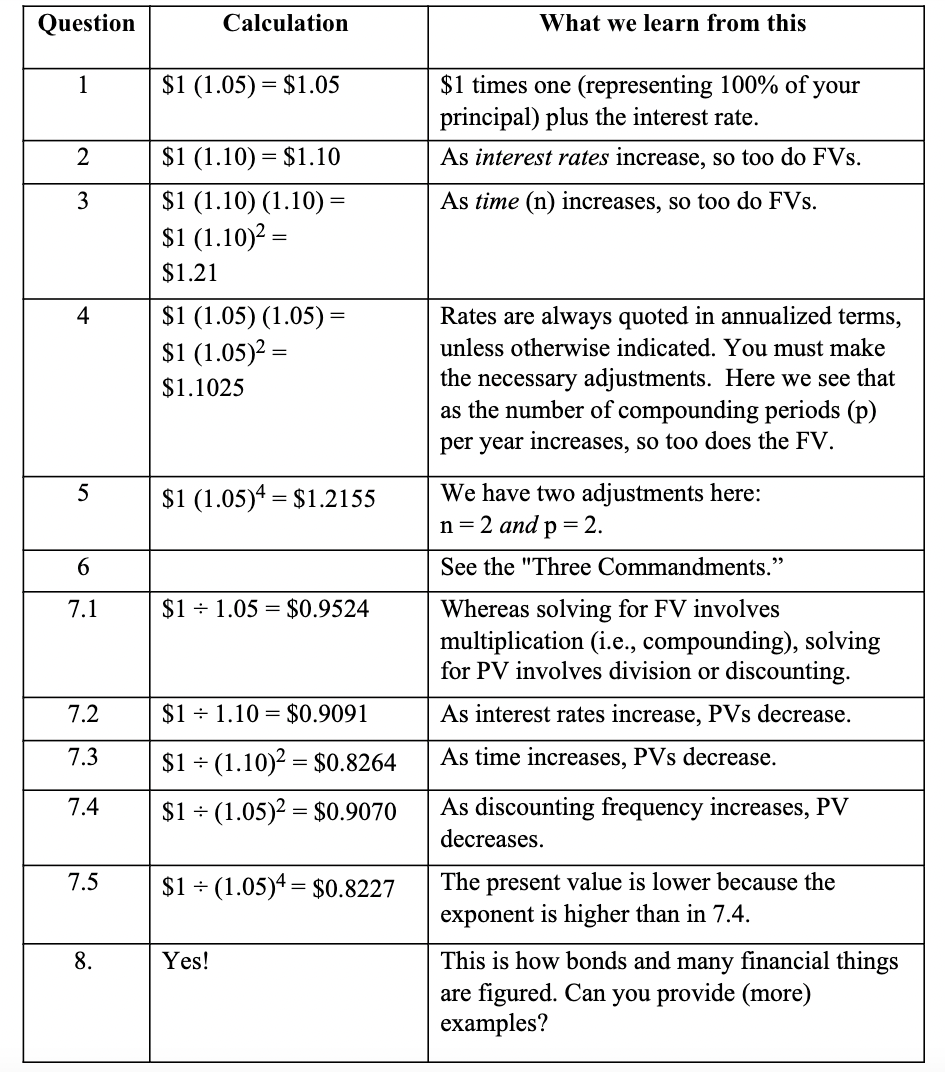
Solutions and Explanations:
The $1 in the question is referred to as Present Value (PV). The amount of money we will have in the future is referred to as Future Value (FV). Remember, we are, so far, assuming that the interest payments are made at the end of each relevant payment period.
An investment in knowledge pays the best interest.
-Benjamin Franklin
