10.3 Interest-on-the-Interest: The Nature of Compound Interest
After one year (as noted in the example above), the investor will have earned $0.10 for every dollar invested at 10%. This was represented by the formula: $1 (1.10) = $1.10.
We noted that if the investor had invested for two years (again at 10% per year) he would have $1.21. This was represented by: $1 (1.10)2 = $1.21. In other words, in the first year, s/he earned $0.10 in interest, while in the second year, he earned $0.11. Why does he earn more interest in the second year if the interest rate – 10% – remains the same?
In the second year, he once again receives $0.10 interest on his principal investment of $1. However, since he has already earned $0.10 of interest from the prior year, he will also earn 10% on that dime! That is equal to another penny of interest earned: ($0.10) (10%) = $0.01. Thus, in the second year he will have earned another $0.10 plus $0.11 or a total of $0.21. The following summarizes this notion:
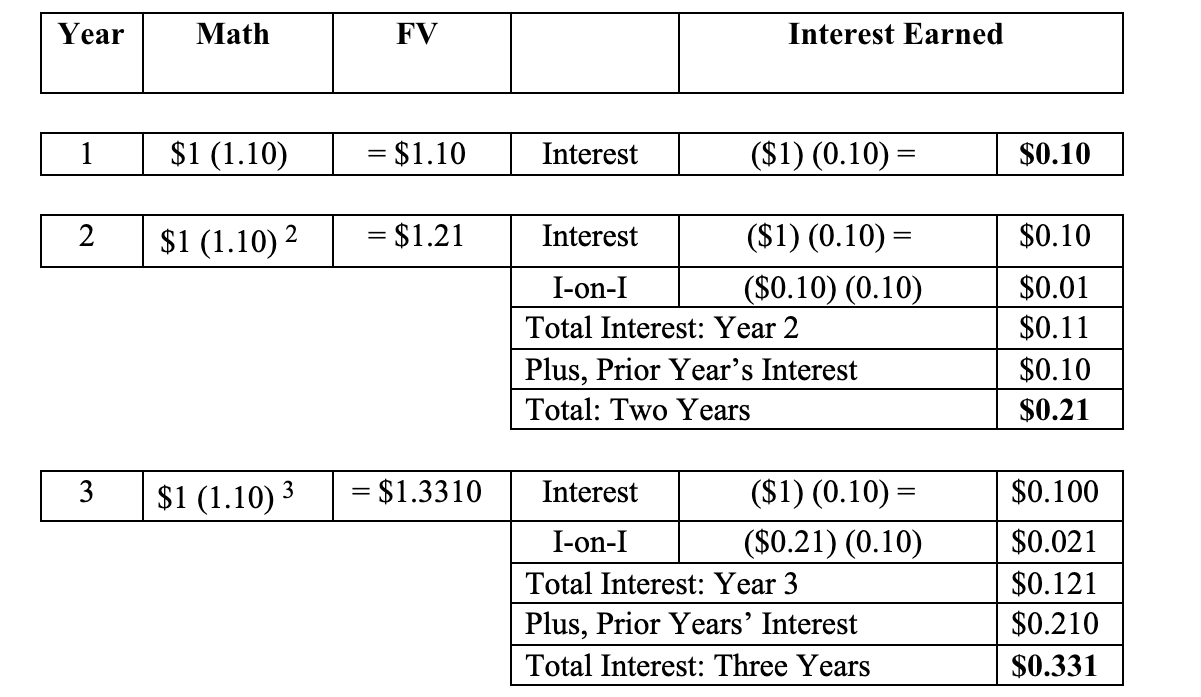
This is the nature of interest-on-the-interest: Compound Interest! Each year, the interest-on-the-interest will continue to compound.
