11.19 The “Law of Limits” and Perpetuities
We have already seen that present value of a perpetuity can be described by the formula: P0 = CF ÷ i. We have also provided both the algebraic derivation of this formula and a discussion as to how the present value of a perpetuity approaches (but never quite reaches) the price described by the formula.
Still, many students find the idea of limits – and of the infinitesimal – difficult to grasp. Our intent here is to further elucidate the notion that present values decrease over time with the result that distant cash flows become so small, so infinitesimal – they have so many decimal places – that they add virtually nothing to the aggregate present value. In making this observation, you will also note that, as a result, the cumulative value of the perpetuity’s present value approaches the theoretical price described by the formula, as posited by mathematicians. This is as it should be.
Let us say that a perpetuity’s cash flows are $1 and the interest rate at which we shall discount the series is 10%. The present value therefore would be: P0 = $1 ÷ .10 = $10. This is confirmed in the table below.
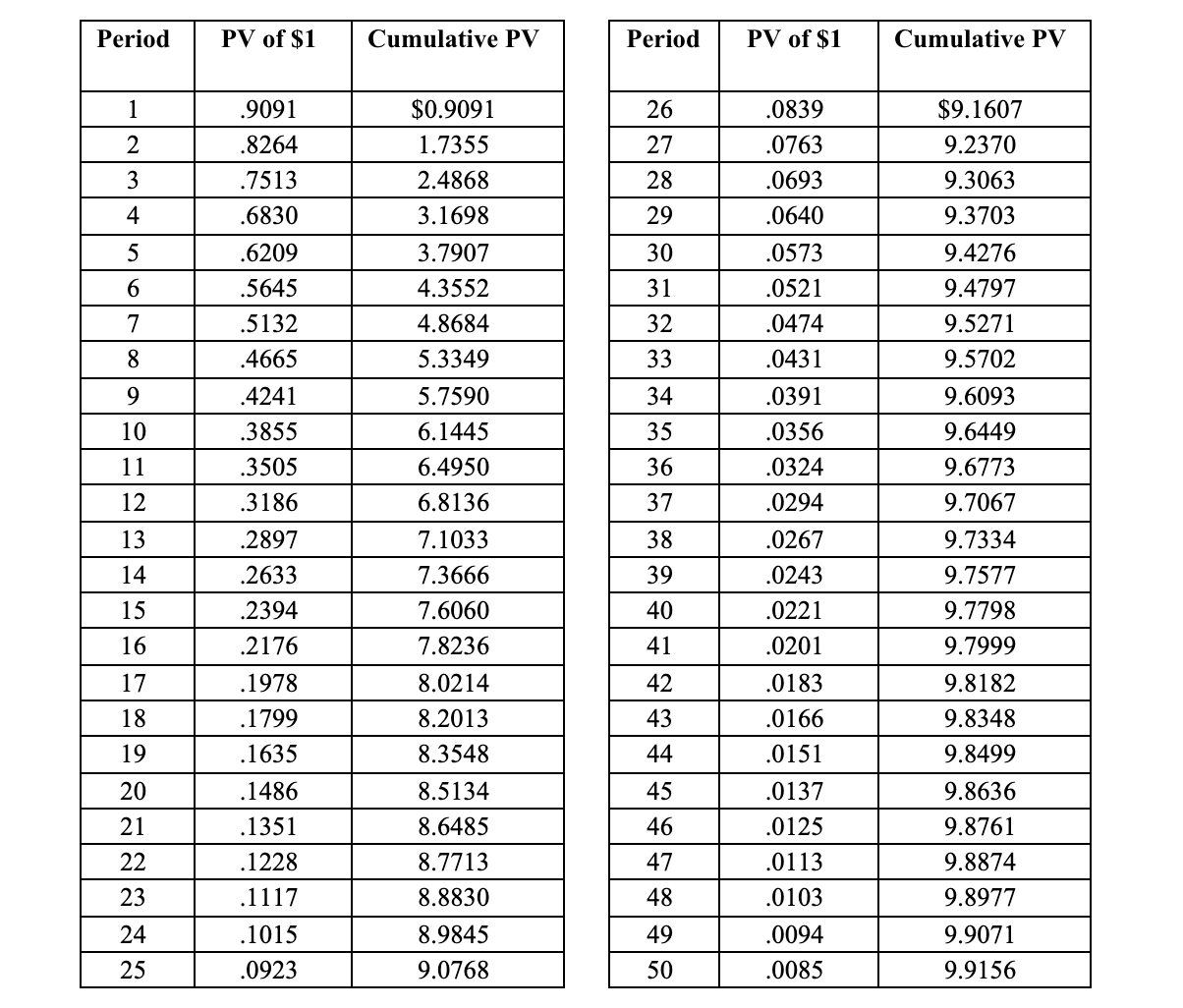
After 25 years, we reach 90% of the aforecited aggregate present value, and by the 50th year, we exceed 99% of the $10 value. With the passage of more time, we shall get closer and closer to $10, but only reach $10 in infinite space.
Perpetuities: Pondering the Infinite
He counts the number of the stars; to all of them, He assigns names.
-Psalms 147:4
Lift high your eyes and see: Who created these? He who sends out their host by count, who calls them each by name: Because of His great might and vast power, not one fails to appear.
-Isaiah 40:26
If you always put limits on everything you do, physical or anything else, it will spread into your work and into your life. There are no limits. There are only plateaus, and you must not stay there, you must go beyond them.
-Bruce Lee
