11.20 Growth Perpetuities

A “growth” perpetuity is a perpetual cash flow stream (CF) that grows at a constant rate of growth, which we shall call “g.” It is a special case of perpetuity. If, in the last period, we received a cash flow of $100 and its growth rate is 5%, the next cash flow would follow this formula: (Last Cash flow: CF0) (1 + g) = Cash flow in next period (CF1). “G” represents a constant rate of growth in the cash flow over time. 

CF1 = CF0 (1 + g)

$105 = $100 (1.05)

The formula for a growth-perpetuity is: (Cash flow next period) ÷ (Discount rate – Growth rate).  Symbolically, this may be expressed as: 

PV = CF1 ÷ (r – g)

In the above example (where r = 0.10), if the growth rate had been 5%, the present value would be (assuming here that the next CF is $105, that is, [$100] [1.05] = $105): 

$105 ÷ (.10 – .05) = $2,100

Notice that for this formula to work, “g” cannot equal or exceed “r.” Mathematically, if g exceeds r we would get a negative denominator, resulting in a negative present value, which makes no sense. A mathematical rationale, while necessary, is however not sufficient to justify this relationship. There must be a financial explanation.   

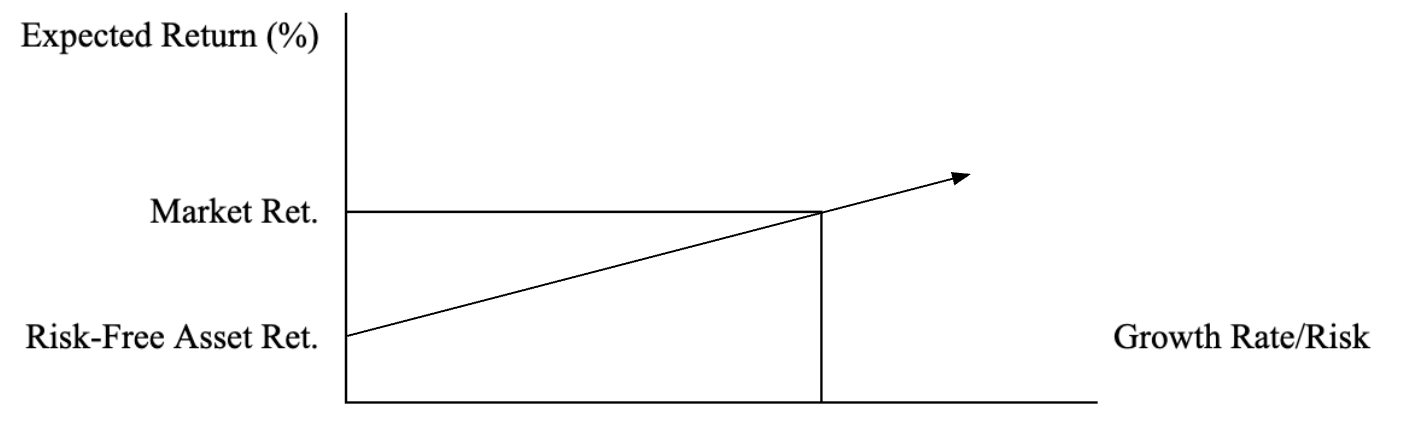
One, theoretically, earns some positive return – “r” – for investing in a no-risk asset[1]; otherwise, no one would invest at all. Even with no risk (and no growth!), there is a positive return. Therefore r > g. As growth rates increase (in linear manner), so too does risk; higher growth rates are more difficult to achieve and hence are riskier. R (“r”) should exceed g, as a practical, non-mathematical matter. This is depicted in the diagram below. 

Key Terms:

Negative Growth

 


This formula may also come in handy for cases of negative growth. Since “g” would be negative, in this case, the formula would require that one add the growth rate to the interest rate in order to determine the present value.

Suppose the last cash flow (CF0) was $100, there is a nominal cash flow growth rate of negative 5%, and a discount rate of 10%. What would the present value be? 

[($100) (1 – (0.05)] ÷ [.10 – (-.05)] =

$95 ÷ .15 = $633.34

Of course, the PV in the case of positive growth far exceeds the outcome we observed with negative growth. Is that not as it should be?

This formula is applicable to common stock, whose dividends may grow – positively or negatively. 

Note:

Looking at this graph alone one may conclude that, at some point, r < g. This is because the line is steeper than at a horizontal plane, thus, there would be less “rise” than “run,” leading eventually to growth exceeding the discount rate, and producing a negative present value. While this may be true if one limits the analysis to the graph alone, it cannot be correct, in fact, that dividend growth is not reflected in return – which is also the discount rate, and part of the denominator. As dividends rise, so too must return. (Remember: discounting and compounding are the same; just the arrows go in different directions.) This anomalous and paradoxical case will be discussed in depth when we discuss the “Dividend Discount Model.” 
  1. As this is being written (2021), we observe an unusual environment wherein interest rates in many parts of the world are negative. ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Financial Analysis Copyright © 2022 by Kenneth S. Bigel is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book