11.22 Loans: The Conventional Mortgage
Mortgages are different from ordinary loans. With most loans, interest is paid over the term, or life, of the loan, and the entire principal is paid in one fell swoop at the loan’s term, or maturity. In contrast, mortgages are self-amortizing, which means that all payments include portions of both interest and principal, resulting in decreasing principal balances over time until, at maturity, the entire loan will have been paid off. Let us see, by way of (an unrealistic) example how this may work.
| Given: | Principal: | $100,000 | Rate: | 9 % |
| Term: | 10 Years | Period: | Yearly |
Mathematical Rationale:
The loan proceeds, i.e., $100,000 in this case, represent the present value. The “periodic payment” represents the annuity payments to be made over future years and will include both Interest and Amortization. Amortization goes toward the reduction of the loan or principal balance. The present value of the annuity payments should equal the loan principal:
Principal = Periodic Payment x Present Value Annuity Factor
Calculation:
Payment = Principal ÷ PV Annuity Factor = $ 100,000 ÷ 6.42 = $ 15,576.32
Interest = Opening Balance × Rate
Amortization = Annuity Payment less Interest
Balance = Opening Balance less Amortization
Payment and Amortization Schedule:
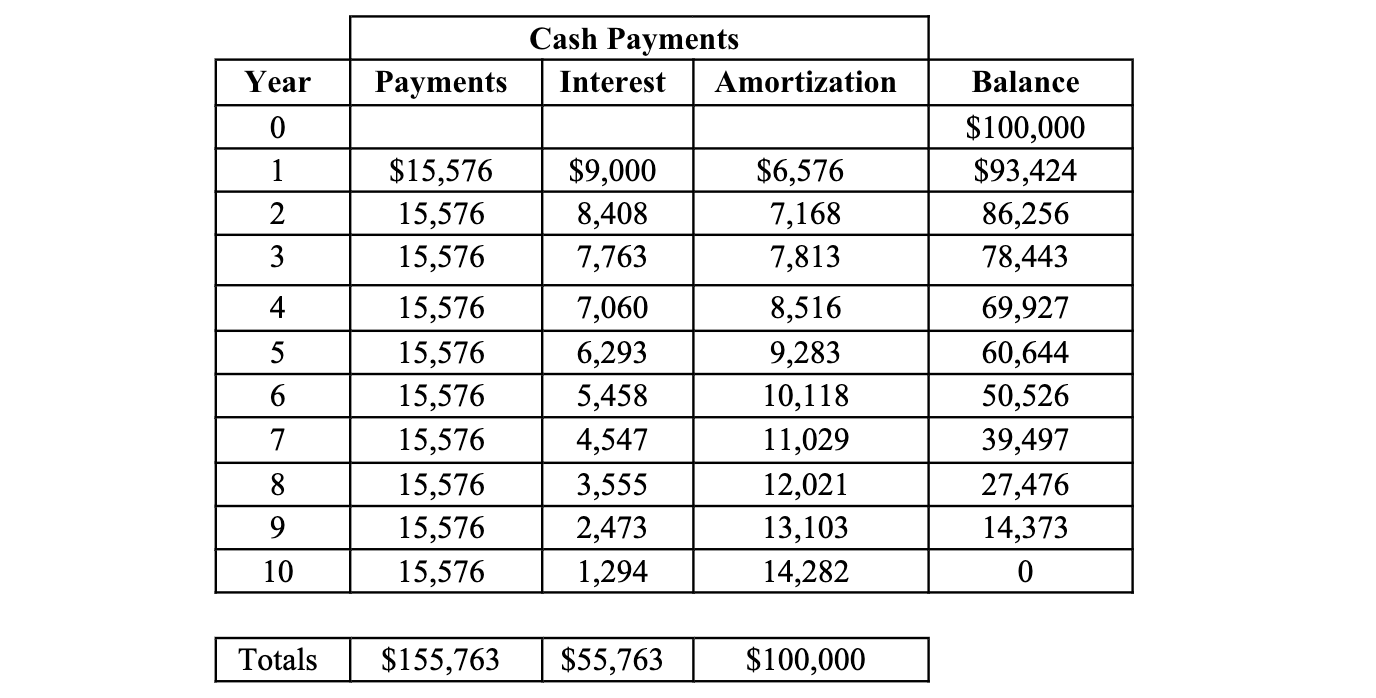
In the first year, the interest portion of the payment is 9% of $100,000 or $9,000. This leaves $15,576 less $9,000 = $6,576 going toward amortization. The new, amortized balance is hence $100,000 less $6,576 = $93,424. Each year the annuity installment is first used to pay the interest on the loan and the balance is used to reduce the capital outstanding. This continues for each period until maturity. In the maturity year the last annuity installment is sufficient to cover the interest still owed and the remaining balance. (You will note a rounded number in the last year.)
Note:
