11.25 Personal Financial Planning Problem

1. This year, Abraham will start graduate school. The annual cost is $30,000 per year for each of two years, payable at the start of the year. 
2. The tuition will increase by 3% in the second year, due to inflation.
3. Abraham currently owes $25,000 from his undergraduate student loans.
4. When he finishes his M.B.A. in two years, his parents will give him a $50,000 gift. 
5. Upon graduation, Abraham plans to pay off his loans fully in ten years. How much will he have to pay annually in order to achieve his goal?  
6. Assume throughout an 8% cost of funds rate, compounded quarterly, except for the annuity payoff payments, which will be at an 8% annual rate.  

Solution Plan: 

• First lay down the given data, in nominal terms, in their proper places in a timeline; then, import the numbers into a spreadsheet.
• Calculate the future value of the costs at the end of year 2, using the cost of funds rate given. Note the gift as money in. 
• Use the mortgage formula to calculate the annuity payment required to pay off the accumulated debts in the last 10 years. 

Solution: 

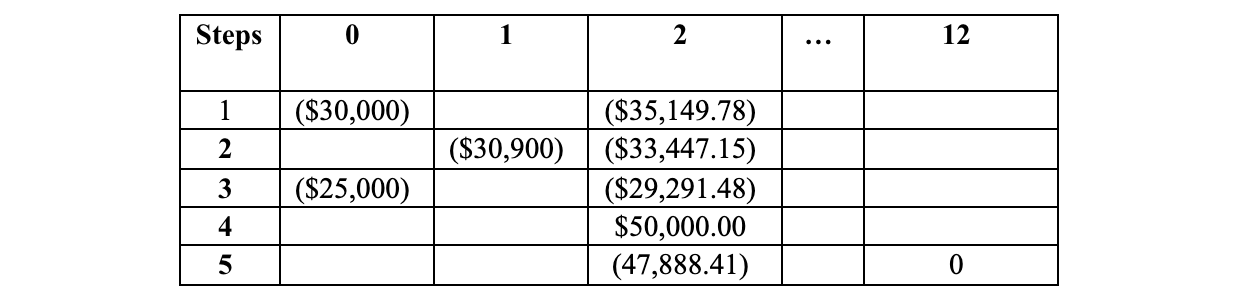
Calculations:

Step 1: ($30,000) (1 + .08/4) ^{2 × 4} = $35,149.78  

Step 2: $30,000 × 1.03 = $30,900

    ($30,900) (1 + .08/4) ^{1 × 4} = $33,447.15 

Step 3: $25,000 × (1 + .08/4) ^{2 × 4} = $29,291.48  

Step 4: $50,000 gift 

Step 5: Sum of Steps 1-4 

Step 6: Calculate the annual annuity payments.