11.6 Future and Present Annuity Factors: Mathematical Formulas
Key: PVAF – Present Value Annuity Factor. FVAF – Future Value Annuity Factor.
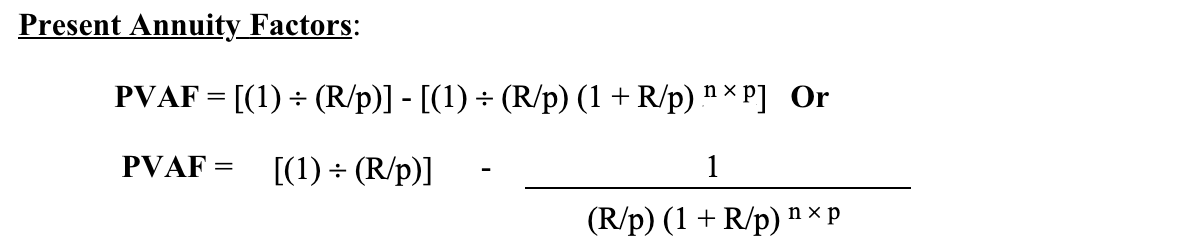
Example 1: R = 0.10; N = 5; P = 2
Solution 1: [(1) ÷ (0.10/2)] – [(1) ÷ (0.10/2) (1 + 0.10/2) 5 × 2] = 7.72173493
*This multiplier should be the same as in your Present Value Annuity Table.
Example 2: R = 0.095; N = 5; P = 2
Solution 2: [(1) ÷ (0.095/2)] – [(1) ÷ (0.095/2) (1 + 0.095/2) 5 × 2] = Fill in your answer
*This multiplier is not in your Present Value Annuity Table. Compare the two solutions.
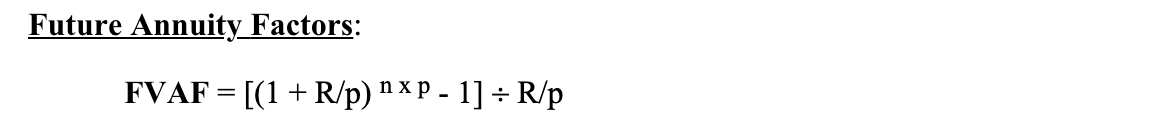
Example 3: R = 0.10; N = 5; P = 2
Solution 3: [(1 + 0.10/2)5 x 2 – 1] ÷ 0.10/2 = 12.57789253554883
*This multiplier should be the same as in your Future Value Annuity Table.
Example 4: R = 0.1012; N = 5; P = 2
Solution 4: [(1 + 0.1012/2) 5 x 2 – 1] ÷ 0.1012/2 = Fill in your answer
*This multiplier is not in your Future Value Annuity Table. Compare the two solutions.
