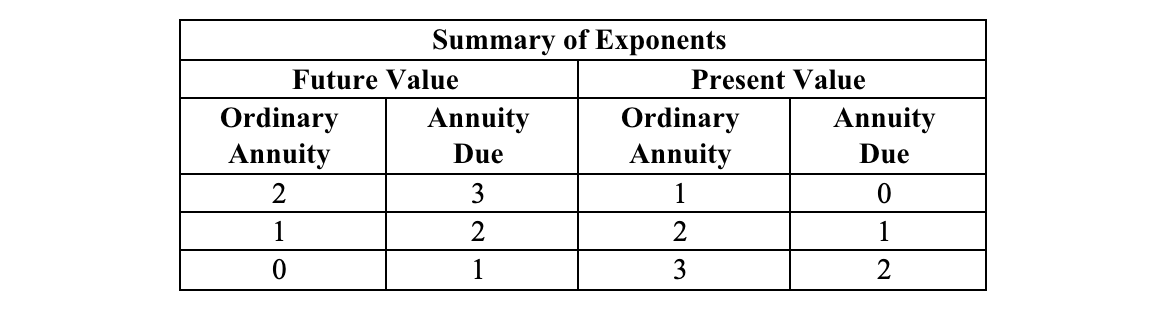
11.11 Adjustment from Ordinary Annuity to Annuity Due
The PV and FV for an ordinary annuity with the same term, rate of interest, and dollar amounts, were calculated earlier at $248.68 and $331 respectively. (See the table at the bottom of this page for a key summary of the differences in exponents.) Since an annuity due provides each of its cash flows one period earlier than the ordinary annuity, the PV and FV of the annuity is equal to the respective ordinary annuity factors multiplied by (1 +R/p)1. (Note that in all instances the exponent is one because the cash flows are pulled ahead just one period.) In this case that would be:
$248.68 (1.10)1 = $273.55
$331.00 (1.10)1 = $364.10
The fact that the cash flows are received (or paid) sooner in the example of an annuity due has an interesting implication (as noted in the adjustment formula above). In the case of the PV, there will be fewer discounting periods than with an ordinary annuity, so the PV will be higher. In the case of the FV, there will be more compounding periods, hence the FV is also higher. Again, in both instances, the ordinary annuity factor is adjusted by a multiple of (1 +R/p)1. Note that even when p ≠ 1, the exponent will always be one, representing just the one period (even if part of a year) in which the series is “pulled ahead.”
Question: How would the adjustment in our example be made if the compounding frequency instead were semi-annual?
Answer: In this case, one would multiply by (1 +R/p)1= (1 + 0.10 / 2)1= (1.05)1.