12.5 Fixed Income Securities: Dollar Price and Yield-to-Maturity
Fixed Income Securities: Dollar Price and Yield-to-Maturity Calculation
Since the coupon cash flow is an annuity, a simple valuation solution would utilize the following formula. Take note, that it does not matter how many zeros you use, although, we shall always figure a face value in this text of $1,000 for consistency and convenience, unless otherwise noted:
Example:
| Coupon | .10 (Semi-annual) |
| Term-to-Maturity | 5 years |
| Market/Discount Rates (Y-T-M) | .08, .10, and .12 |
You’ll need calculators and interest rate tables for this!
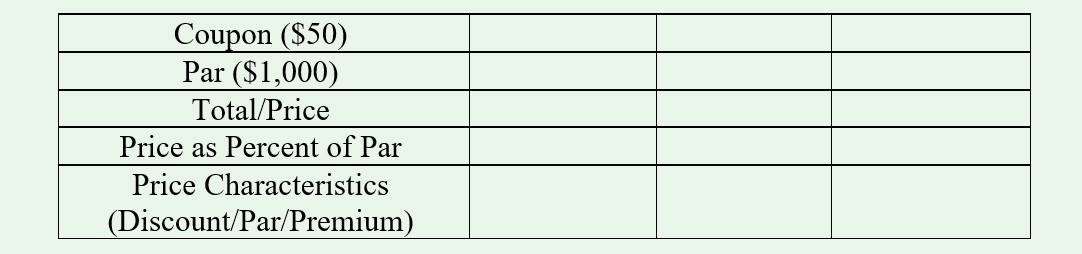
Discount Rates
Here you shall need to insert the appropriate present value annuity factor (PVAF) for the coupon and the present value factor (PVF) for the Maturity Value. Do not forget to make the proper adjustments for semi-annual discounting.

Dollar Values
Here you shall need to multiply the above factors by the dollar amounts of the coupon/annuity and face value respectively.
The “true” price of the bond may, in fact, be considered the YTM. It is conceivable that there exist two bonds with the same maturity (or even issued by the same company) but due to having been issued at different times, the two bonds carry different coupons. Thus, the YTM will be the same for each, but the dollar prices will be different. Therefore, YTM is the true market price, at which bonds’ values are assessed.
Question: What would the prices be if the above bond’s coupon were 0%?
Answer: The PV of just the Face Value at the appropriate YTM / Discount Rate.
Fixed Income Securities: Dollar Price and Yield-to-Maturity (Solution)
It is important not only to solve problems, but to interpret them as well.
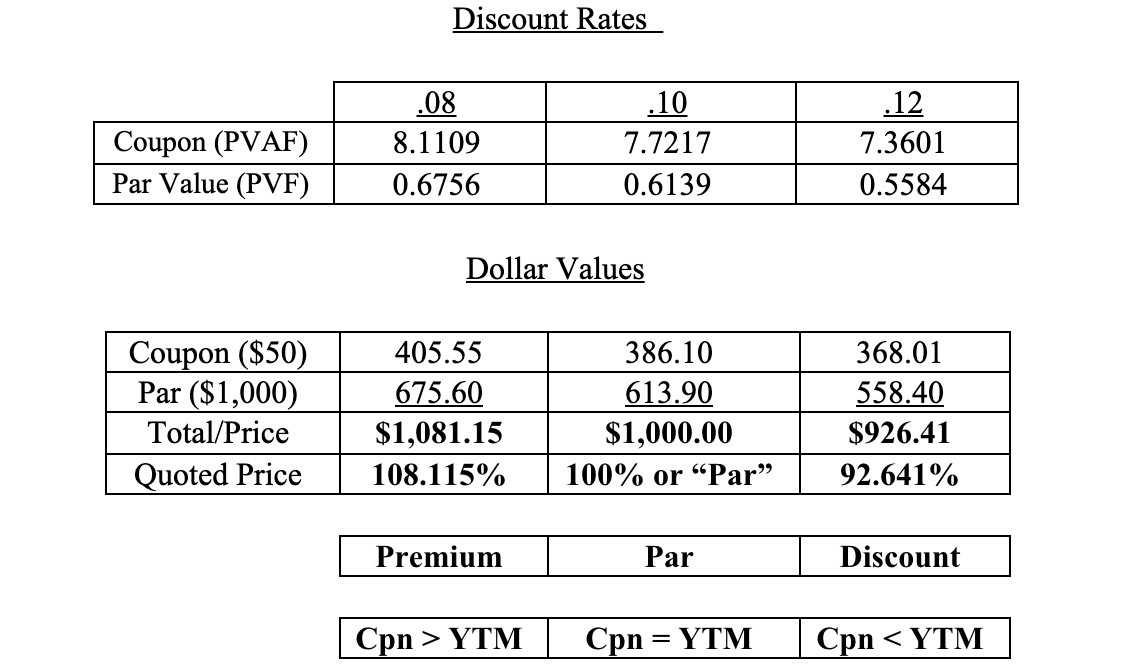
- Note that this illustration has used ordinary annuity factors, rather than only simple present value factors.
- The “Quoted Price” is stated as a Percent of Par.
- Premium/(Discount):
- You get more (less), you pay more (less)!
- You get more (less) coupon than the current market yields, you pay more (less)!
It is interesting to note, for instance, using the discount bond above, that the future value of the bond’s price equals the future value of its cash flows. 926.41 (1.7908) = $50 (13.181) + 1,000.
