13.2 Interest Rates: Returns to Investors; Cost to the Corporation
Interest rates, and, hence securities’ returns, are a function of economic circumstances that are manifest in the financial markets. Return to investors represents cost to the corporations that issue the securities; they are the two sides to the same coin. As in the case of “return on investment,” the phrases “return” and “cost of capital” to a corporation are described in percentage terms, i.e., as a rate, and not as a dollar amount. Cost of capital refers to the weighted-average cost of the corporation’s debt and equity.
Both debt and equity provide the corporation with funds with which to acquire assets, so that the corporation may grow. Investors who provide these funds to the corporation expect a return on their investment; this return represents an “economic cost” to the corporation. The money is not free. “Economic Cost” is a financial term, not an accounting term such as “expense,” and should be understood differently.
- The cost of debt capital to the corporation is the after–tax cost of interest paid on the debt.
Key Terms:
Cost of Debt Capital
Cost of Equity Capital
- The cost of equity capital includes the dividends paid to investors plus their expectations of capital gains resulting from the growth in earnings. Remember, shareholders may expect to receive dividends and to see additions to retained earnings. Should the investors’ expectations, which we may also view as their minimum required return, not be met, they may sell the security.
Investors expect that retained earnings and other capital sources be productively employed in the growth of the company so that their shares’ value increases – due to increased earnings and growth expectations. Corporations therefore must provide the assurance of price appreciation, or shareholders will sell, and/or hire new managers and directors. This prospective price appreciation is also part of the firm’s capital costs, as viewed from the economist’s eye.
Required Return
Risk-free Rate of Return
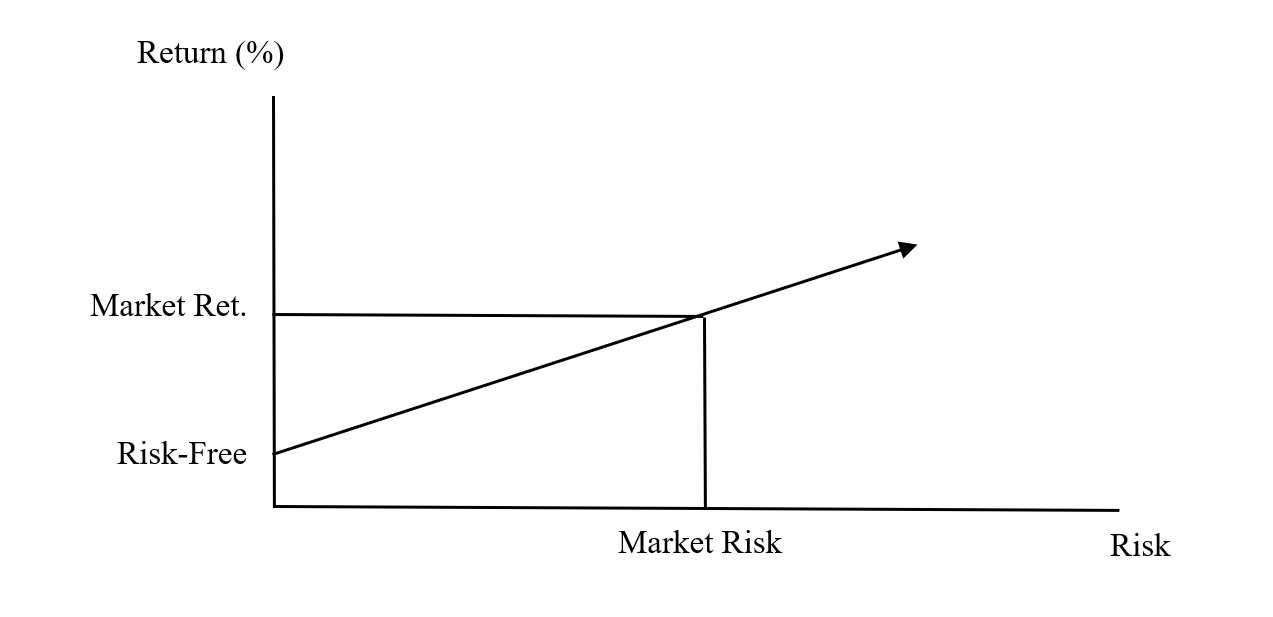
In general, the required return (R) whether for stocks or bonds, consists of two parts: one, a return associated with the “risk-free” instrument and the risk-free rate of return (RF); the other, a premium, or extra, return for incremental risk above zero-risk. That is, the required return equals the risk-free rate of return plus a “market risk premium” (MRP).
R = RF + MRP
MRP = RM – RF
Here, you will find a graph that depicts these concepts.
-
- The phrase “risk premium” (referring to RM – RF) is a bit of a misnomer, as the term “risk” draws your attention toward the horizontal axis rather than the vertical axis where the premium (-return for incremental risk) is observed.
-
- The “Market Risk Premium” (MRP) = Market Return (RM) less Risk-free Rate-of-Return (RF).
- In the graph above, we have risk (a quantifiable measure) and return, which is measured in percentage terms. We also have the overall or average “market risk” and its corresponding market return.
There is also a theoretical zero-risk investment and its corresponding risk-free rate of return. Even though the zero-risk investment has no risk (excuse the redundancy), it still provides a positive rate of return. If it provided no return, no one would invest in it. There is no agreement about the real-world proxy for the risk-free instrument; it is usually taken as either the three-month Treasury Bill, or the ten-year Treasury Note. More precisely, the risk-free instrument’s expected and required returns will be the same, and the standard deviation of its return will be zero.
Again, the Market Risk Premium (MRP) will be the difference between the risk-free and market rates of return. In other words, the market return provides a premium or additional return to the investor for taking on a level of risk greater than zero. Any particular investment, or portfolio of investments, may provide more, or less, risk and return than the overall market.
In such cases, the investor’s portfolio may contain a level of risk greater than or less than the market’s risk level, i.e., to the right or left of the Market Risk on the horizontal axis. Accordingly, the investor may expect to earn more than the market return, or less. The investor’s expected return will then be either above or below the Market Return on the vertical axis. Can you draw this? What would be the investor’s Portfolio Risk Premium?
Rational Expectations
Portfolio Risk Premium
Take note, once again, of the odd use of the term “risk premium” relative to additional return. The more risk one takes on, the proportionally greater should the return be. This is due to the notion of Rational Expectations. One might say that to accept more risk for no added return is irrational, and no one would do that. That is why the slope of the diagonal is positive. The diagonal market line in the diagram reflects this positive risk/reward relationship. The more the risk, the more the (expected) return.
- Many researchers will use the 3-month Treasury Bill as the proxy for the theoretical risk-free instrument. This choice has to do with three explanations.
-
- First, the United States Treasury is considered the least risky of all debtors (although that may no longer be true).
- Second, because the 3-month term is so short, market price fluctuation is not at issue; in a very short while, the bills will mature and pay their full, face value.
- Third, Liquidity is also enhanced by the sheer size of the Treasury market itself; size comes with greater trading volume and hence more liquidity.
- Not all agree about the risk-free proxy. Some argue for the use of the 10-Year Treasury Note as the real–world equivalent of the risk-free instrument. This is because Equities tend to be longer-term investments and, more importantly, because Credit Spreads (to be discussed in a later chapter) are usually figured in a ten-year timeframe.
The sages of Yavne used to say: I am a creature of G-d and my neighbor is also;
my work is in the city and his is in the field;
I rise early to work and he rises early to his.
As he cannot excel in my work, I cannot excel in his.
But you may be tempted to say,
‘I do great things and he small things!’
We have learned that it matters not whether one does much or little,
if only he directs his heart to heaven.
-Babylonian Talmud
Tractate Berachoth, 17a
