14.10 A Closer Look at Dividend Growth
In order to fully understand the “g” term in the dividend discount model, a term which is not intuitive, let us have a closer look. (As you go through this example, keep in mind that, as the company retains earnings the balance sheet gets “bigger.”) We are given the following information about a company:
If:

Then:
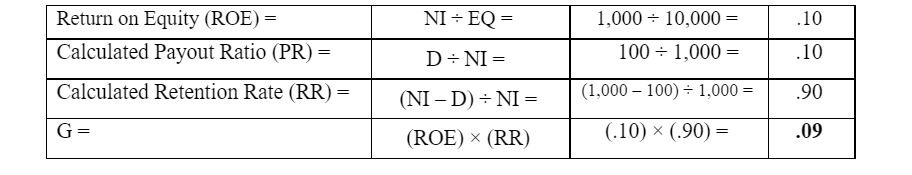
Given this information, G = (ROE) × (RR) = (.10) × (.90) = .09. By definition, G, the growth rate in the dividend, must also be defined, far more simply, as: G = [(D1) ÷ (D0)] – 1. This simple formula is readily understood. Remember that G = ARE / NI, or the rate at which the Equity grows. Take note that, here, we have assumed that G, ROE, and RR are constants.
Let’s see if the two formulae work out to be the same; if so, we will therefore also know that the “G = (ROE) (RR)” formula makes sense, given the same data. Let’s see first how the simple formula, G = [(D1) ÷ (D0)] – 1, works out using an accounting–type (i.e., chronological) approach.
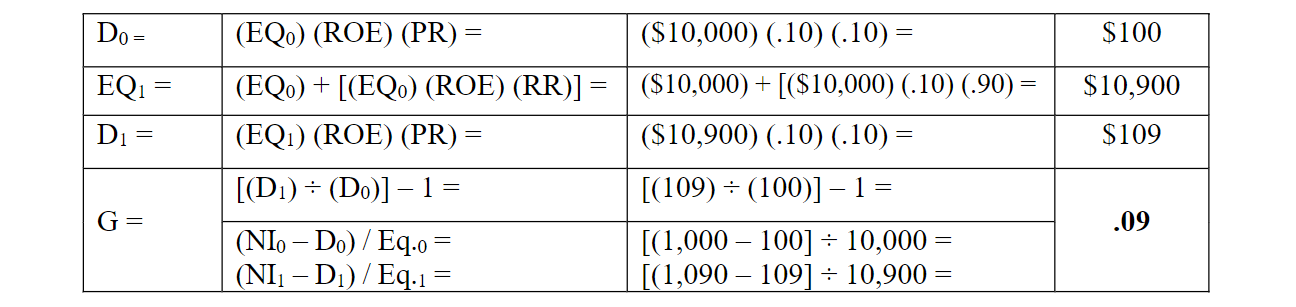
This gets us the same result – as it should! (In fact, we could not have known the value of D1 had we not had the first formulation!) This notion assumes that the retention rate (and payout ratio), dividend growth rate, and ROE are constants. You’ll note that the equity is growing at the same rate of 9%. This latter table says that if we earn and retain earnings, we will be able to pay out more money in dollars as dividends later.
To assist you with the above formulae:
(EQ) (ROE) = (EQ) (NI / EQ) = NI and
(NI) (PR) = (NI) (D/NI) = D
