14.15 Capital Gains
It is interesting to note that, if G > 0, the model will automatically generate capital gains. Here again is our formula. Below is a problem whose resolution illustrates the model’s automatic generation of capital gains.
Question:
Formula:
P0 = [D0 (1 + G)] / (R – G)
P0 = D1 / (R – G)
Given:
D0 = $1 The Last Dividend
R = 10% The Discount Rate
G = 5% The Dividend’s Constant Growth Rate
What is the price today?
What would the price be in one year?
Solution:
P0= $1 (1 + .05) / (.10 – .05)
= 1.05 / .05
= $21
Price in One-Year:
P1 = D2 / (R – G)
P1 = $1.05 (1 + .05) / (.10 – .05)
= 1.1025 / .05
= $22.05
We observe that $22.05 / $21 = 1.05. That is to say that next year’s price will be greater than last year’s by 5%, or the same as the stock’s growth rate (again, assuming a constant pay-out ratio).
We often say that a stock is “ahead of itself,” if the rate of growth in price exceeds the dividend – or earnings – growth rate (assuming a constant pay-out ratio).
Capital Gains, Dividend Growth: Some Practice Problems
The following should help summarize some relevant concepts.
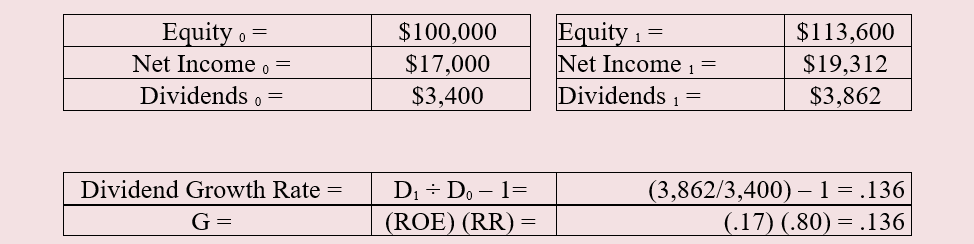
1. Complete the empty cells, given the data noted below for a stock. The basic formula for the Dividend Discount Model is:
P0 = [(D0) (1 + G)] ÷ [R – G]
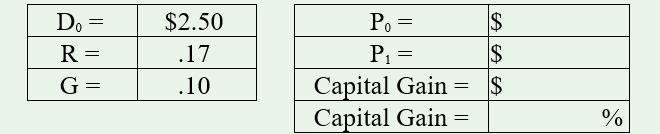
2. Once again, complete the spreadsheet, given the data noted for a particular stock.
Given:
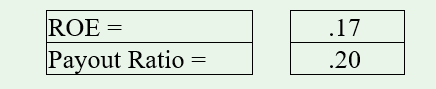
Solve:
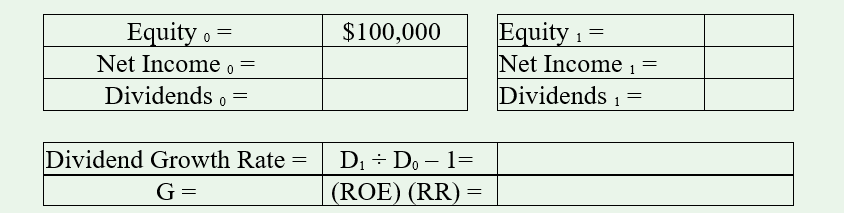
- Explain, in words, what is meant by the term, “G,” in question #2.
- Assuming G is a constant (question #1), P0 (1 + G) = P1.
Capital Gains, Dividend Growth: Some Practice Problems (Solutions)
Problem 1:
 Problem 2:
Problem 2: