14.16 Portfolio Return (Weighted Averages)
Now that we know all about individual bond and stock returns, what about portfolios of securities? A portfolio is a collection of individual securities.
If the market values of the portfolio’s constituent securities were the same, the portfolio weights would be equal, and the simple arithmetic- and weighted-averages would be the same. In calculating the simple arithmetic return, one would take the observed returns and divide by the number of observations. Here, the weights are unequal, so we must employ a weighted average calculation as below.
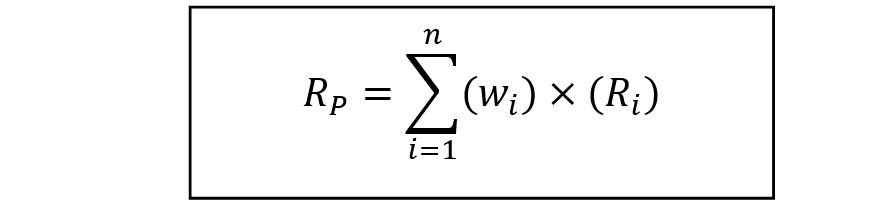
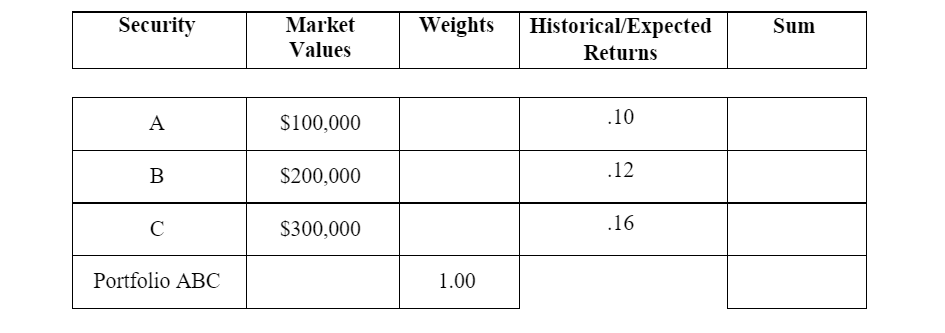
Example: Calculate the (historical or expected) weighted average return for the following portfolio, which consists of three securities (A, B, and C) and has the market values and individual returns as noted.
Note: Portfolio risk is not simply a weighted-average of the portfolio constituents’ respective risks – due to “covariance” among securities.
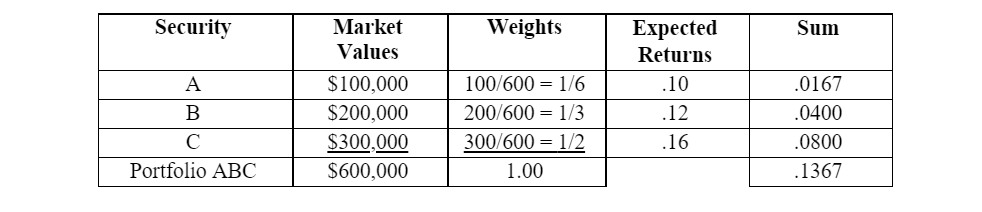
Portfolio Return (Solution to Problem)
Solution (table form):
Solution (by formula):
RP = 1/6 (.10) + 1/3 (.12) + 1/2 (.16) = 0.1367
Short-cut solution:
RP = [(100) (.10) + (200) (.12) + (300) (.16)] ÷ 600 = 0.1367
In the short-cut solution, we do not take the weights first. Instead, we multiply the dollar values by each expected return and, at the end, divide by the entire portfolio value.
The 0.1367 return means that the investment would increase by 13.67% in one year. If you had invested $1,000, after one year’s time, you would have one thousand dollars plus $136.70 for a total of $1,136.7. Some of the return, presumably, would come from income (rent, interest, or dividends) and some from capital growth (price appreciation). The constituent security returns, as given here, were themselves represented without any further detail as to the breakdown of income and growth portions.
If the weights had all been equal (i.e., .3333, in this case), we could have calculated a simple average by adding the sum of the returns and dividing by (n =) 3. In other words, a simple average implies equal weights.
If one of the constituent security’s returns were negative, we would of course get a different result. Let us say that the return on Security “A” were -.10, rather than positive. In this case, the portfolio return would be:
RP = 1/6 (-.10) + 1/3 (.12) + 1/2 (.16) = .1033
Another way in which we could have calculated this would have been as follows:
0.1367 – (2) (.0167) = .1033
