14.4 The Dividend Discount Model (DDM): Fixed Dividend or No- Growth Version
We shall assume that the security’s Intrinsic Value (V) will be equal to the market price (P), i.e., that P = V. Intrinsic value refers to what the security is “truly” worth. To the extent that P ≠ V, one would be presented with the opportunity to earn an extraordinary profit (by either buying cheaply or selling “richly”). Hereforward, we shall use P rather than V, although you may see V used elsewhere.
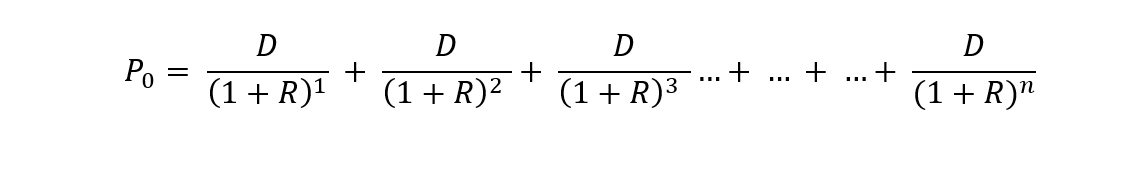
A stock is a kind of perpetuity; the corporation, as a going concern, is eternal. Dividends will be paid in perpetuity. Unlike bonds, there is no face value to be paid at a specified time in the future. The only cash flows are the dividends.
This formula says that the price of a stock is equal to its aggregated discounted future cash flows, i.e., the dividends discounted to present value. Since, for the moment we assume that dividends are fixed (as in a preferred stock), the foregoing, never-ending equation may be simplified algebraically to the following (as was demonstrated for a perpetuity, only the terms have been modified to accommodate stock):
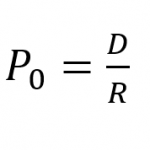
This simplification works because of the “Law of Limits,” discussed earlier in our TVM section. Interestingly, by transposing, the above formula may be re-formulated as:
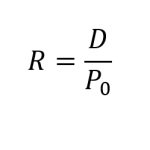
Note: D ÷P is the Dividend Yield!
While corporations pay dividends quarterly, the formula looks at annual dividends. Recall that, in the case of a perpetuity, discounting frequency has no effect on Present Value.
