14.5 The Dividend Discount Model (DDM): Constant Growth Version
a.k.a. “The Gordon Model”
Of course, not all stocks pay fixed dividends. Let us take a small step forward and assume that the dividend grows – at a constant rate of growth. In this version of the Dividend Discount Model (DDM), the constant dividend growth rate is designated as “G”:
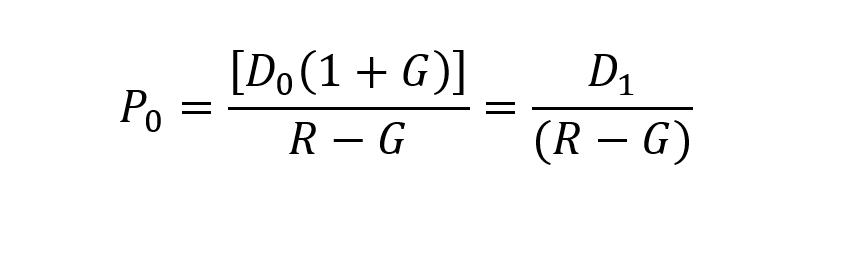
This formula is identical to a constant growth perpetuity. The nomenclature was altered here in order to suit common stocks. With some simple algebraic transposition, we can re-formulate the DDM so as to isolate the discount rate to one side:
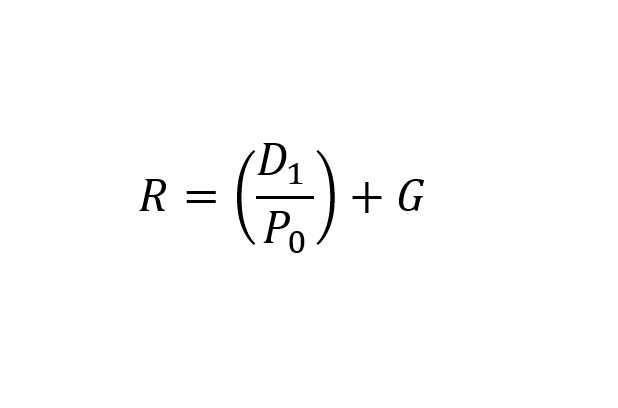
Code: D0 = the last reported Annual Dividend (i.e., the sum of the last four, quarterly dividends)
D1 = D0 (1 + G)
G = the imputed growth rate for dividends.
Note, interestingly, that this means that the discount rate is equal to the sum of the dividend yield plus the growth rate in dividends. This formulation presents a percentages view on the model; all terms are percentages.
Note also that when G = 0, we have the “no-growth” version of the DDM. If G > 0, we have the “Constant-Growth” DDM. As discussed in the TVM section, R must exceed G for both practical / financial and mathematical reasons. Remember that when we speak of “growth,” we refer to growth in dividends, which, in turn, comes from growth in sales and profits.
Questions:
Given: R = .15 D = $1.50 G = 0
- What is the price?
- What happens to P if R goes down?
- What happens to P if G goes down?
Solutions:
-
P = ($1.50) / .15 = $10
-
Just as in the TVM, as the discount rate decreases, present values (P) increase. So too here!
-
“R – G” increases, and D1 decreases, both of which result in, or cause, a lower price
Note:
This version of the DDM is a.k.a. “The Gordon Model,” named after Myron Gordon. This idea is not without its controversy or weaknesses, the discussion of which is beyond our current scope.
